Властивості операцій над множинами
Для будь-яких
множин А,
В
і С
із
справедливі співвідношення
1. Закон тотожності (ідемпотентності):
,
,
але
,
.
2. Закон комутативності (переміщуваності):
,
,
,
але
(оскільки
,
).
3. Закон асоціативності (сполучуваності):
,
,
,
але
(оскільки
,
).
4. Закон дистрибутивності (розподільності):
, ,
,
,
, ,
,
але
,
,
,
,
5. Закони нуля й одиниці:
,
,
,
,
,
,
,
.
6. Властивості доповнення:
,
,
(закон інволютивності,
подвійного заперечення),
,
,
,
.
7. Закони де Моргана (принцип подвійності, двоїстості):
,
.
8. Закони поглинання:
,
,
,
.
9.
Якщо
,
то
,
,
.
10. ,
,
.
Характеристичні функції
,
,
,
,
,
,
,
.
————————————————
Логічні функції від двох аргументів:
Набір значень |
Формула |
Назва функції (прочитання її формули) |
|
х |
0011 |
||
y |
0101 |
||
|
0000 |
0 |
Константа нуль, тотожний нуль (константа нуль) |
|
0001 |
|
Кон’юнкція, логічний добуток, логічне множення, логічне І, функція збігу (x і y) |
|
0010 |
|
Заборона y, заперечення імплікації, антиімплікація (x і не y; x, але не y; неправильно, що з х випливає y) |
|
0011 |
|
Повторення x, домінація першого аргументу (як х) |
|
0100 |
|
Заборона x, заперечення зворотної імплікації, зворотна антиімплікація (не x і y; не x, але y; неправильно, що з y випливає х) |
|
0101 |
|
Повторення y, домінація другого аргументу (як y) |
|
0110 |
|
Додавання (сума) за модулем 2, розподільна диз’юнкція, виключене АБО, заперечення еквівалентності, функція нерівнозначності (x не як y; або x, або y; x не еквівалентне y) |
|
0111 |
|
Диз’юнкція, логічна сума, логічне додавання, логічне АБО, функція поділу (x або y) |
|
1000 |
|
Функція (стрілка) Пірса, функція Вебба, штрих Лукасевича, заперечення диз’юнкції, антидиз’юнкція (не x і не y) |
|
1001 |
|
Еквівалентність, еквіваленція, логічна рівнозначність (x як y; x тоді і тільки тоді, коли y; x еквівалентне y) |
|
1010 |
|
Заперечення y, інверсія y (не y) |
|
1011 |
|
Зворотна імплікація, імплікація y в x (x, якщо y; якщо y, то x; з y випливає х; x або не y) |
|
1100 |
|
Заперечення x, інверсія х (не х) |
|
1101 |
|
Імплікація x в y, матеріальна імплікація (якщо x, то y; з х випливає y; не x або y) |
|
1110 |
|
Функція (штрих) Шеффера, заперечення кон’юнкції, антикон’юнкція (не x або не y; x і y несумісні; неправильно, що x і y) |
|
1111 |
1 |
Константа 1, тотожна одиниця (константа один) |
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Двоїсті функції:
0 і 1, х
і х,
і
,
і
,
і
,
і
,
і
.
Подання елементарних
функцій через операції
:
,
,
,
,
,
,
,
,
.
Подання елементарних
функцій через поліноми Жегалкіна:
,
,
,
,
,
,
,
,
.
Таблиця істинностей основних функцій від двох аргументів:
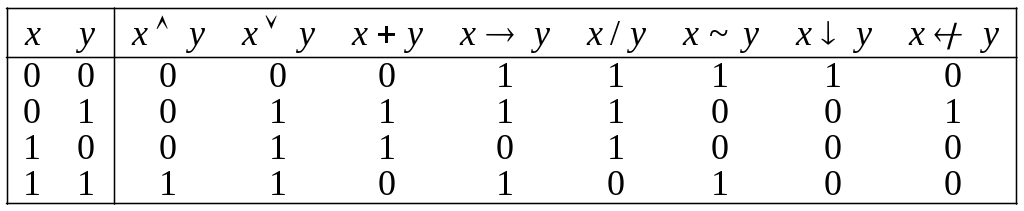
Належність до замкнених класів:
Функції |
Набір значень |
Замкнені класи |
|||||
|
|
S |
M |
L |
|||
Нульарні |
|||||||
0 |
0 |
+ |
– |
– |
+ |
+ |
|
1 |
1 |
– |
+ |
– |
+ |
+ |
|
Унарні |
|||||||
х |
01 |
+ |
+ |
+ |
+ |
+ |
|
|
10 |
– |
– |
+ |
– |
+ |
|
Бінарні |
|||||||
|
0001 |
+ |
+ |
– |
+ |
– |
|
|
0111 |
+ |
+ |
– |
+ |
– |
|
|
0110 |
+ |
– |
– |
– |
+ |
|
( ) |
1101 (1011) |
– |
+ |
– |
– |
– |
|
|
1110 |
– |
– |
– |
– |
– |
|
|
1001 |
– |
+ |
– |
– |
+ |
|
|
1000 |
– |
– |
– |
– |
– |
|
( |
0100 (0010) |
+ |
– |
– |
– |
– |
|
)
Правила поглинання
і склеювання:
— поглинання;
— склеювання;
— неповне склеювання;
— узагальнене
склеювання.
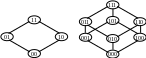
Булів куб: Карти Карно:
———————————————————
Пошук вглиб
В алгоритмі пошуку вглиб використовується стек, який працює за принципом LIFO (last in — first out), тобто додавання й вилучення елементів стеку відбувається з одного кінця — верхівки стеку.
Для простого зв’язного неорієнтованого графа алгоритм пошуку вглиб передбачає таку послідовність кроків:
К1. Довільній вершині v присвоюємо номер 1 і записуємо позначку цієї вершини в стек;
К2. Нехай у верхівці
стеку є вершина
.
Якщо всі ребра, інцидентні вершині
,
позначено, то переходимо на К4, інакше
— на К3;
К3. Нехай
— непозначене ребро. Якщо вершині
номер присвоєно, то ребро
позначаємо, наприклад, пунктиром (- - -)
і переходимо на К2. Якщо вершині
номер не присвоєно, то присвоюємо їй
поточний номер і записуємо її позначку
в стек; ребро
позначаємо, наприклад, суцільною товстою
лінією (——)
і переходимо на К2.
К4. Вилучаємо з верхівки стеку позначку вершини . Якщо стек порожній, то каркас побудовано (його вершини перенумеровано, а ребра позначено суцільною товстою лінією); інакше переходимо на К2.
Пошук вшир
В алгоритмі пошуку вшир використовується список-черга, яка працює за принципом FIFO (first in — first out), тобто елементи додаються в хвіст черги, а вилучаються з голови. При виборі вершин з голови розглядаються всі ще не занумеровані її сусіди.
Для простого зв’язного неорієнтованого графа алгоритм пошуку вшир передбачає таку послідовність кроків:
К1. Довільній вершині v присвоюємо номер 1 і записуємо позначку цієї вершини в чергу;
К2. Нехай на початку черги є вершина . Якщо всі ребра, інцидентні вершині , позначено, то переходимо на К4, інакше — на К3;
К3. Нехай — непозначене ребро. Якщо вершині номер присвоєно, то ребро позначаємо, наприклад, пунктиром (- - -) і переходимо на К2. Якщо вершині номер не присвоєно, то присвоюємо їй поточний номер і записуємо її позначку в чергу; ребро позначаємо, наприклад, суцільною товстою лінією (——) і переходимо на К2.
К4. Вилучаємо з початку черги позначку вершини . Якщо черга порожня, то каркас побудовано (його вершини перенумеровано, а ребра позначено суцільною товстою лінією); інакше переходимо на К2.
———————————————————