1.5. Расчёт баланса мощностей цепи
Суммарная мощность в ваттах источников ЭДС, с учётом того, что источник Е2 работает в режиме потребителя:
>> Pi =(E3*I3)-(E2*I2)
Pi =
26.2110
Суммарная мощность потребителей в ваттах:
>> Pp =I1^(2)*R1+I2^(2)*R2+I3^(2)*R3+I4^(2)*R4+I5^(2)*R5+I6^(2)*R6
Pp =
26.2122
Баланс мощностей с точностью до сотых ватта сходится.
1.6. Расчёт тока i1 по методу эквивалентного генератора
На рис.
1.5 приведена цепь, в которой отключен
резистор R1
между узлами “a”
и “d”.
Необходимо преобразовать эту схему в
цепь эквивалентного генератора
с внутренним сопротивлением
и последовательно включенным резистором
R1,
а также рассчитать ток I1.
Рассчитаем напряжение в вольтах между узлами “c” и ”b”, используя метод двух узлов, при заданных значениях R2=7,5Ом, R3=3Ом, R4=12Ом, R5=16,5Ом, R6=22,5Ом, E2=18B, E3=30B.
>> R2=7.5;
>> R3=3;
>> R4=12;
>> R5=16.5;
>> R6=22.5;
>> E2=18;
>> E3=30;
>> Ucb = ((E3-E2)/(R2+R3))/(1/(R2+R3)+1/(R4+R6)+1/R5)
Ucb =
6.1833
Рис. 1.5. Схема электрической цепи
Определим токи в ветвях цепи в амперах (рис. 1.5):
>> I4.6=Ucb / (R4+R6)
I4.6 =
0.1792
>> I2.3 = ((E3-E2)-Ucb)/(R2+R3)
I2.3 =
0.5540
По второму закону Кирхгофа определим ЭДС эквивалентного генератора равную напряжению холостого хода в вольтах из уравнения:
Uad + I23*R3 + I46*R6 = E3
>> Uad = E3 - ((I23*R3) + (I46*R6))
Uad =
24.3055
Для определения цепь рис. 1.5 преобразуем в цепь рис. 1.6, в которой ЭДС Е2 и Е3 равны нулю. Затем в цепи рис.1.6 треугольник сопротивлений R4, R5, R6 преобразуем в схему эквивалентной звезды Ra. Rb, Rc (рис. 1.7), где сопротивления эквивалентной звезды в омах определяются по формулам:
>> Ra = (R4*R6)/(R4+R5+R6)
Ra =
5.2941
>> Rb = (R4*R5)/(R4+R5+R6)
Rb =
3.8824
>> Rc = (R5*R6)/(R4+R5+R6)
Rc =
7.2794
Внутреннее
сопротивление
в омах эквивалентного генератора
относительно зажимов a
– d
определяем по формуле:
>> R0 = Ra + ((Rb+R2)*(Rc+R3))/(Rb+R2+Rc+R3)
R0 =
10.6955
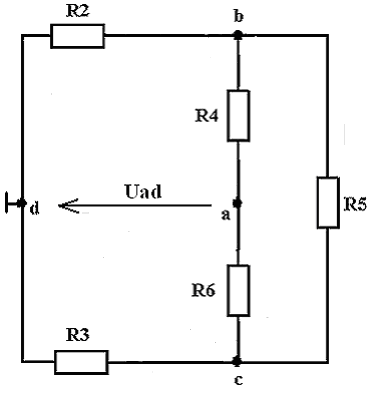
Рис. 1.6. Схема электрической цепи
Рис. 1.7. Схема электрической цепи
Схема эквивалентного генератора Еэкв = Uad в вольтах с внутренним сопротивлением R0=Rэкв, питающая резистор R1=19,5Ом, приведена на рис. 1.8, откуда определяем ток I1 в амперах.
Рис. 1.8. Схема электрической цепи
>> Uad = 24.3055
Uad =
24.3055 В
>> I1 = Uad / (R0+R1)
I1 =
0.8049A,
что соответствует действительности.
Электрические цепи переменного тока Задача 2
2.1. Условия задачи
Рассмотрим
электрическую цепь переменного тока,
схема которой приведена на рис. 2.1, в
которой заданы элементы цепи: катушки
с индуктивностями
;
конденсатор
;
резистор R3=25(Ом);
источники ЭДС переменного тока
,
,
;
частота питающей сети f
= 1000(Гц); угловая частота
.
Необходимо, используя комплексный метод расчёта цепей синусоидального тока, определить комплексные значения токов ветвей цепи, рассчитать баланс мощностей источников и потребителей цепи.