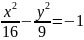Блок «Гипербола»

Задача 1

Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:

• Её оси 2a=10 и 2b=8;

• Расстояние между фокусами 2c=10 и ось 2b=8;

• Расстояние между фокусами 2c=6 и эксцентриситет = ;

• Ось 2a=16 и эксцентриситет = ;

• Уравнения асимптот и расстояние между фокусами 2c=20;

• Расстояние между директрисами равно и расстояние между фокусами 2c=26;

• Расстояние между директрисами равно и ось 2b=6;

• Расстояние между директрисами равно и эксцентриситет = ;

• Уравнения асимптот и расстояние между директрисами

равно .

Ответ:

• 

• 

• 

• 

• 

• 

• 

Задача 2

Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что:

• Её полуоси a=6, b=18 (буквой “a” мы обозначаем полуось гиперболы, расположенную на оси абсцисс);

• Расстояние между фокусами 2c=10 и эксцентриситет = ;

• Уравнения асимптот и расстояние между вершинами равно 48.

• Расстояние между директрисами равно и эксцентриситет = ;

• Уравнения асимптот и расстояние между директрисами

равно .

Ответ:

• 

• 

• 

• 

Задача 3

Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты её центра C, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис:

1. 16 -9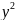 -64x-54y-161=0

2. 9 -16 +90x+32y-367=0

3. 16 -9 -64x-18y+199=0

Ответ:

1)C(2;-3), a=3, b=4, 5/3, уравнения директрис: 5х-1=0, 5х-19=0, уравнения асимптот: 4x-3y-17=0, 4x+3y+1=0;

2)C(-5;1), a=8, b=6, =1,25, уравнения директрис : x=-11,4 и x=1,4, уравнения асимптот: 3x+4y+11=0 и 3x-4y+19=0

3) C(2;-1), a=3, b=4, =1,25 , уравнения директрис: y= -4,2 , y=2,2 , уравнения асимптот: 4x+3y-5=0, 4x-3y-11=0

Блок «Прямые в пространстве»

Задача 1

Составить канонические уравнения прямой, проходящей через точку (2;0;-3) параллельно:

1. Вектору a=

2. Прямой -= =

3. Оси Ox

4. Оси Oy

5. Оси Oz

Ответ:

• 1) -= =

• -= =

• -= =

• -= =

• -= =

Задача 2

Составить параметрические уравнения прямой, проходящей через данные точки:

1. (3;-1;2), (2;1;1)

2. (1;1;-2), (3;-1;0)

3. (0;0;1), (0;1;-2)

Ответ:

• x=t+2, y=-2t+1, z=t+1

• x=t+3, y=-2t-1, z=5t-3

• x=0, y=t, z=-3t+1

Задача 3

Через точки (-6;6;-5) и (12;-6;1) проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.

Ответ: (9;-4;0), (3;0;-2), (0;2;-3)

Задача 4

Найти острый угол между прямыми -= = , -= =

Ответ:

Задача 5

Найти проекцию точки P (2;-1;3) на прямую x=3t, y=5t-7, z=2t+2

Ответ: (3;-2;4)

Задача 6

При каких значениях L и C прямая = =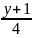 перпендикулярна к плоскости 3x-2y+Cz+1=0

Ответ: L=-6, C=

Задача 7

Найти точку Q, симметричную точке P (4;1;6) относительно прямой x-y-4z+12=0, 2x+y-2z+3=0

Ответ: Q (2;-3;2)

Задача 8

Найти точку Q, симметричную точке P (2;-5;7) относительно прямой, проходящей через точки (5;4;6) и (-2;-17;-8)

Ответ: Q (4;1;-3)

Задача 9

Найти проекцию точки P (5;2;-1) на плоскость 2x-y+3z+23=0

Ответ: (1;4;-7)

Задача 10

Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:

1. -= = ; -= =

2. x=2t-4, y=-t+4, z=-2t-1

x=4t-5, y=-3t+5, z=-5t-1

3. -= = ;

X=6t+9, y=-2t, z=-t+2

Ответ:

1. 13

2. 3

3. 7