Линейные операции над векторами
Задача 1
Дано:
Найти:
Ответ: 22
Задача 2
Дано:
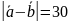
Найти:
Ответ: 20
Задача 3
Даны
2 вектора
(3;-2;6) и
(-2;1;0).
Определить
проекцию на координатную ось
.
Ответ:
.
Задача 4
Проверить коллинеарность векторов (2;-1;3) и (-6;3;-9). Установить какой из них длиннее и во сколько раз.
Как они направлены: в одну или противоположные стороны?
Ответ:
Вектор длиннее вектора в 3 раза.
Задача 5
Определить
при каких значениях
векторы:
коллинеарны.
Ответ:
Задача 6
Проверить, что точки А (3;-1;2), В (1;2;-1), С (-1;1;-3), D (3;-5;3) служат вершинами трапеции.
Задача 7
Даны 3 вектора а (3;-1), b (1;-2), c (-1; 7).
Определить
разложение вектора
=
по
базису
.
Ответ:
p=
-3
Задача 8
Даны
4 вектора
(2;1;0),
(1;-1;2),
(2;2;-1),
(3;7;-7).
Определить разложения каждого из этих 4-х векторов принимая в качестве базиса 3 остальных.
Ответ:
2
-3
-c
-2 +3 +
+
-
Скалярное произведение векторов
Задача 1
Векторы
взаимно перпендикулярны,
образует с ними угол
.
Зная,
что
=3,
=5,
=8
вычислить:
1)(
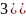
Ответ: 1)-62, 2)162, 3) -34
Задача 2
Векторы
попарно образуют друг с другом углы,
каждый их которых равен
.
Зная, что
=4,
=2,
=6,
определить
=
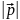Ответ: 10.
Задача 3
Векторы
образуют угол, равный
.
Зная, что
=
,
=1,
вычислить угол между векторами:
р=
;
р=
Ответ:
.
Задача 4
Даны векторы (4;-2;-4), (6;-3;2).
Вычислить
;
(
(
.
Ответ: 22;-200, 129
Задача 5
Даны
силы
(2;3;-5),
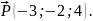Вычислить,
какую работу производит равнодействующая
этих сил, когда её точка приложения
двигаясь прямолинейно перемещалась из
положения
(5;3;-7) в положение
.
Ответ: 13.
Задача 6
Даны
вершины треугольника:
Определить его внутренний угол при
вершине В.
Ответ:
Задача 7
Найти
вектор
коллинеарный вектору
и удовлетворяющий условию
Ответ: 56
Задача 8
Даны
векторы
Найти
вектор
удовлетворяющий условию:
∙
=-5,
∙
=-11,
∙
=20.
Ответ: (2;3;-2).
Задача 9
Вычислить проекцию вектора с координатами (5;2;5) на ось вектора с координатами (2;-1;2)
Ответ: 6.
Задача 10
Даны
вектора
Вычислить
проекцию
на вектор
.
Ответ: -4.
Задача 11
Даны
точки
(-2;3;-4),
(3;2;5),
(1;-1;2),
(3;2;-4).
Вычислить
проекцию вектора
на вектор
.
Ответ:
.
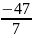Векторное произведение векторов
Задача 1
Даны
векторы
= 10,
= 2,
= 12.
Найти
.
Ответ: 16
Задача 2
Даны векторы = 3, = 26, = 72.
Найти .
Ответ:
Задача 3
Векторы
и
образуют угол
.
Зная, что = 1, = 2, вычислить:
и
.
Ответ: 3 и 10
Задача 4
Даны вектор (3;-1;-2) и (1;2;-1).
Найти
,
.
Ответ: 1) (5;1;7), 2) (10;2;14), 3) (20;4;28).
Задача 5
Даны точки А (2;-1;2), В (1;2;-1), С (3;2;1).
Найти
координаты векторных произведений
и (
-2
)
.
Ответ: (6;-4;-6) (-12;8;12).
Задача 6
Даны точки А (1;2;0), В (3;0;-3), С (5;2;6).
Вычислить площадь треугольника АВС.
Ответ: 14
Задача 7
Даны вершины треугольника точки А (1;-1;2), В (5;-6;2), С (1;3;-1). Вычислить длину его высоты, опущенной из вершины В на АС.
Ответ: 5
Задача 8
Вычислить sin угла, образованного векторами (2;-2;1), (2;3;6).
Ответ:
.