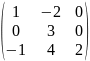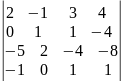Блок «Матрицы»

1. А_nxn=(a_ij)

Сколько элементов расположено:

• Над главной диагональю:

• На главной диагонали:

• Под главной диагональю:

Ответ:

На главной диагонали:

Под главной диагональю: :

Над главной диагональю: :

2. Запишите матрицы А_3x3 элементы, которых a_ik определяются по форме:

1. a_ik=i+k;

2. a_ik=i∙k

3. a_ik=(i-k)²

4. a_ik=i²k+ik²

Совпадают ли элементы этих матриц расположенных симметрично относительно главной диагонали.

Ответ:

1. A=

2. A=

3. A=

4. A=

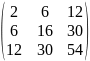
Да, совпадают.

3. Для каких матриц А_mxn существуют A+A^T

Ответ:

Для квадратных матриц.

4. Найти матрицу Х удовлетворяющую условию 3A+2X=E, где Е – единичная матрица 3-его порядка и матрица А равна:

А=

Ответ:

Х=

5. Известно, что A_2x3∙B_mxn=С_2x6. Найти m и n.

Ответ:

m=3; n=6

6. Даны матрицы A_2x3, B_3x1,C_3x3. Существую ли произведения: АВ, ВA, AC, CA, ABC, CB, CBA, АСВ.

Ответ:

Существуют: АВ, AC,АСВ,СВ;

Не существуют: ВА, СА, АВС, СВА.

7. Найти сумму матриц А+В, разность А-В, произведение А∙В и В∙А, если существует:

• А= 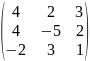В=

• А= В=

• А= В=

• А= В=

• А= В=

• А= В=

Ответ:

• A+B= A-B=

AB= BA=

• Не существует;

• Не существует;

• АВ=

• AB= BA=

• AB= A-B=

8. Найдите все матрицы перестановочные с матрицей:

А=

Ответ:

B=

9. Вычислить степень приведённых ниже матриц:

• 

• 

• 

• 

Ответ:

1. 

2. 

3. 

4. 

10. Используя равенства:

= ;

.

Вычислите

Ответ:

11. Докажите, что если матрицы А и В – перестановочные, то выполняется

(А+В)²=А²+2АВ+В²

(А+В)(А-В)=А²-В²

Верны ли эти равенства, если матрицы не являются перестановочными?

Ответ:

Если матрицы не перестановочные, равенство не выполняется.

12. Доказать, что если первая и вторая строки матрицы А равны, то первая и вторая строки матрицы АВ, так же равны.

13. Найдите f(A), если А=

1. f(x) = x²-2x+5

2. f(x)=x²-5x+10

3. f(x)=(2x⁵-4x²+7)∙(x²-5x+10)+x+5

Ответ:

1. 

2. .

3. 

14. Вычислить определитель:

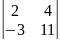
Ответ:

1. 11

2. -2

3. 34

4. 2b-a

5. 1

6. 100

7. -1

8. 27

15. Вычислить определитель αA, если α= , а det А_5x5=3

Ответ: 6

16. Дано:

185;

518;

851.

Докажите что определитель делится на 37 не вычисляя.

17. Вычислить определитель, раскладывая по элементам строки или столбцы, предварительно преобразовав их. Используя свойство определителя.

    1. 

2. 

3. 

4. 

5. 

6. 

7. 

Ответ:

1. 900

2. 297

3. 150

4. -35

5. 12

6. 8

7. -140

18. Вычислить определитель, предварительно преобразовав его.

1. 

2. 

Ответ:

1. 97

2. 110

3. 12

4. -84

19. Найти матрицы обратные данным. Полученный результат проверить, используя определение обратной матрицы

• А=

• А=

• А=

• А=

Ответ:

1. 

2. 

3. 

4. 

20. Проверить системы уравнений на совместность и в случае данных систем уравнений, решить их:

• Методом Гауса

• Методом Крамера

• Матричным методом

1. 

2. 

3. 

4. 

5. 

Ответ:

1. x=1 y=0 z=2

2. x= y= - z= -

3. Решений нет

4. Решений нет

5. x= y=1 z= -

21. Решить системы уравнений Методом Гауса;

1. 

2. 

3. 

4. 

Ответ:

1. Нет решений

2. x₁=1 ; х₂=0 ;х₃=-1 ;х₄=2

3. x₁=0 ; х₂=6 ;х₃=1 ;х₄=2 ;х₅=1

4. x_{1= ;} х₂=R; x_{3= ;} х₄=R

22. Решить системы уравнений и найти нормированную фундаментальную систему решений:

1. 

2. 

3. 

Ответ:

1. 

2. 

3. НФСР – не существует. Решение тривиальное.