Задача 6.

Для виготовлення трьох видів виробів І, ІІ, ІІІ мале підприємство використовує три типи устаткування, ресурс якого складає, відповідно, 360, 192 та 180 станко-годин. Від реалізації одиниці продукції І-го виду можна отримати прибуток 9 грн., ІІ-го – 10 грн., а ІІІ-го – 16 грн. Відома матриця технологічних коефіцієнтів , де – кількість годин, яка потрібна для виготовлення одиниці -го виробу на устаткуванні -го типу: . 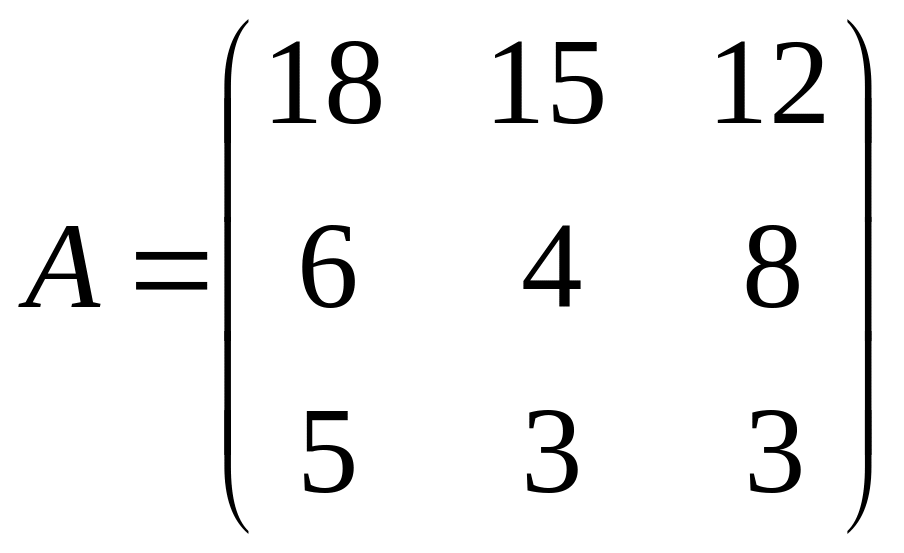Побудувати математичну модель задачі, яка дозволить скласти план використання устаткування, за яким підприємство отримає найбільший прибуток від реалізації готової продукції.

ДОДАТКОВІ ЗАВДАННЯ:

№1: Кондитерська фабрика для виготовлення трьох видів пастили А, В, С використовує три основні види сировини: цукор, фруктове пюре та молоко. Норми витрат на виготовлення 1 т. пастили кожного типу приведені в таблиці:

Види сировини	Норми витрат сировини (т) на 1т видів пастили			Запаси сировини
	А	В	С
Цукор	0,6	0,8	0,5	600
Фруктове пюре	0,4	0,2	0,1	400
Молоко	0,2	0	0,3	160
Прибуток від реалізації 1 т продукції (грн.)	98	122	116

Побудувати математичну модель задачі.

№2: Для виготовлення двох видів продукції Р₁ та Р₂ використовують три види сировини S₁, S₂, S₃. Всі дані наведені у таблиці: \

Види сировини	Кількість одиниць сировини, використаної для виготовлення одиниці продукції		Запаси сировини
	Р1	Р2
S1	1	7	50
S2	2	5	70
S3	5	6	40
Прибуток від одиниці продукції, грн.	40	30

Побудувати математичну модель задачі.

№3: Для виготовлення трьох видів продукції А, В, С використовують фрезувальне, токарне, зварювальне та шліфувальне обладнання. Витрати часу на обробку одного виду продукції та загальний фонд робочого часу для кожного типу обладнання наведені в таблиці:

Тип обладнання	Витрати часу (стан.-часів) на обробку одного виду продукції			Загальний фонд робочого часу обладнання (час.)
	А	В	С
Фрезувальне	3	7	6	280
Токарне	2	8	5	140
Зварювальне	6	4	3	340
Шліфувальне	5	1	2	220
Прибуток	12	10	15

Побудувати математичну модель задачі.