Работа № 6 проверка закона ома для цепи переменного тока

Задание: проверить выполнение закона Ома для переменного тока в цепях с различными нагрузками, а также определить параметры R (омическое сопротивление), L (индуктивность) и С (емкость) этих цепей.

Оборудование и принадлежности: установка для проведения измерений.

Описание установки

Установка предназначена для экспериментального подтверждения закона Ома путем измерения значений тока и напряжения и графического отображения зависимости этих величин от времени.

Установка представляет собой микропроцессорную систему, позволяющую производить аналогоцифровое преобразование входных сигналов напряжений и токов, действующих в цепи выбранных нагрузок с последующим отображением одного полного периода синусоидальных сигналов на экране графического дисплея.

Общий вид установки показан на рисунке 1.

Н а передней панели прибора расположены следующие элементы управления и информации:

• Галетный переключатель позволяет выбрать одну из семи исследуемых нагрузок.

• Кнопками [1] и [20] перемещается реперная линия вдоль горизонтальной оси времени.

• Кнопка [ENTER] позволяет вывести на экран графического дисплея графики U=U(t) и i=i(t).

• Кнопка [PRINT] выводит информацию о проведенных измерениях на принтер.

• На символьном дисплее отображаются величины мгновенных значений тока и напряжения (сила тока в мА, напряжение в В) в зависимости от выбранной точки шкалы времени.

Переменные токи. Закон Ома

При рассмотрении цепей переменного тока мы будем исходить из нескольких предположений.

1.Электрическое напряжение u, подводимое к цепи изменяется со временем t по гармоническому закону:

, (1)

где u - мгновенное значение напряжения, U₀ - максимальное (амплитудное) значение,  - циклическая (круговая) частота. Такое допущение справедливо, так как промышленные генераторы электростанций вырабатывают переменный ток, зависящий от времени, практически, по гармоническому закону. Кроме того, математические операции с гармонически изменяющимися величинами довольно просты, а любое негармоническое колебание можно по теореме Фурье представить в виде суммы гармонических колебаний.

2. Рассматриваемые переменные токи - квазистационарные (как бы стационарные), т.е. время релаксации цепи  (время, в течение которого электрические величины во всей цепи принимают установившиеся значения) намного меньше периода колебаний тока .

Время релаксации для любой цепи определяется скоростью распространения электромагнитного поля, и поэтому для цепи переменного тока с частотой   50 Гц условие квазистационарности выполняется, практически, для цепей протяженностью до 300 км. Соответственно для цепи переменного тока в лабораторной установке условие квазистационарности выполняется с очень большой точностью.

3. Изучаемые периодические процессы являются установившимися, т.е. с момента начала электрических колебаний прошло достаточно большое время, для того чтобы амплитуда напряжения и тока достигли своих постоянных значений. Поэтому в дальнейшем в ходе решений соответствующих дифференциальных уравнений не рассматриваются те решения, которые дают значение величин быстро убывающих со временем (экстратоки).

4. В изучаемых цепях переменного тока включены элементы, каждый из которых обладает одним наиболее выраженным параметром. Реальные приборы и устройства электрической цепи обладают сопротивлением, которое характеризует противодействие кристаллической решетки проводников направленному движению зарядов. Они могут обладать как емкостными свойствами (способность накапливать заряды), так и индуктивными свойствами (возникновение ЭДС самоиндукции).

Для упрощения расчетов принимают, что емкостными свойствами обладает только конденсатор, индуктивные свойства присущи только соленоиду (катушке индуктивности). Т.е. индуктивность и емкость как бы сосредоточены в соленоиде и конденсаторе, соответственно, а сопротивлением току, обусловленном кристаллической решеткой их проводников можно пренебречь. Соответственно, под резистором понимают элемент, практически, не обладающий емкостными или индуктивными свойствами.

Р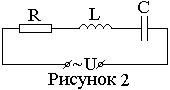 ассмотрим цепь (рисунок.2) с последовательно соединенными резистором R, соленоидом с индуктивностью L и конденсатором емкостью С, которые называют, соответственно, активной, индуктивной и емкостной нагрузками. Пусть цепь подключена к источнику напряжения u, заданного уравнением (1).

Поскольку напряжение зависит от времени, то в цепи возникает переменный ток, а в этом случае в катушке возникает ЭДС самоиндукции. Тогда мгновенные значения силы тока в цепи и напряжения на резисторе и емкости будут определяться суммой напряжения, подведенного к цепи и ЭДС самоиндукции:

, (2)

где i, u_C и e_{L —} мгновенные значения тока в цепи, напряжения на конденсаторе и ЭДС самоиндукции в катушке.

Напряжение на конденсаторе u_C выразим через заряд конденсатора q и его электроемкость C:

. (3)

Электродвижущую силу самоиндукции e_L определим по закону Фарадея:

. (4)

Тогда с учетом соотношения (3) и (4) уравнение (2) запишется в виде:

. (5)

После дифференцирования равенства (5) по времени получим дифференциальное уравнение для нахождения тока i в цепи:

. (6)

Решение этого уравнения будем искать в виде периодической (гармонической) функции той же частоты , что и напряжение, но отличающейся от него по фазе:

, (7)

где I₀ – амплитуда силы тока, а  – сдвиг (разность) фаз между напряжением и током в цепи, которые не зависят от времени.

Для их определения продифференцируем уравнение (7) и подставим в уравнение (6) значения i, di/dt и d²i/dt². После алгебраического преобразования получим

. (8)

Тригонометрические преобразования косинуса и синуса разности двух углов позволяет привести это уравнение к виду:

. (9)

Уравнение (9) представляет собой линейную комбинацию cost и sint, которая равняется нулю в любой момент времени t. А это возможно только при равенстве нулю обоих коэффициентов, стоящих перед этими функциями. Следовательно,

, (10)

. (11)

Из равенства (11) сразу находится уравнение для определения сдвига фаз :

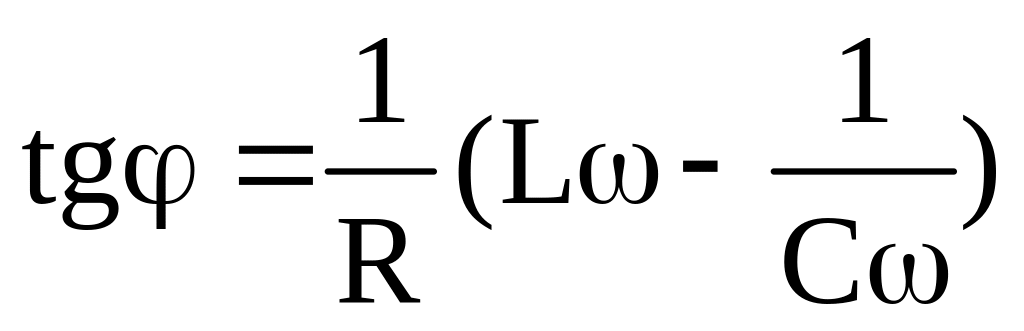. (12)

Для нахождения амплитуды тока I₀ нужно равенства (10) и (11) возвести в квадрат и почленно сложить. Тогда получим

. (13)

Равенства (7), (12) и (13) определяют искомое решение для тока в цепи. Таким образом, в цепи течет ток i, изменяющийся со временем по закону синуса с такой же циклической частотой , что и приложенное напряжение u. Фаза силы тока в общем случае не совпадает с фазой напряжения. Сдвиг фаз , как видно из соотношения (12), зависит от параметров R, L, и C участка цепи, а также от круговой частоты  тока, текущего в этом участке.

Амплитуда силы тока I₀ прямо пропорциональна амплитуде приложенного напряжения U₀, т.е. для амплитудных значений выполняется закон Ома.

Важно отметить, что формула (13) справедлива для амплитуд тока I₀ и напряжения U₀, а не их мгновенных значений i и u.

Измерительные приборы, амперметры и вольтметры, показывают не мгновенные, а действующие значения тока и напряжения I = I₀/2 и U = U₀/2, для которых также справедливо полученное соотношение, т.е.

. (14)

Это закон Ома для действующих значений тока и напряжения в цепи переменного тока. Отношение напряжения U к силе тока I определяет полное сопротивление (импеданс) рассматриваемого участка цепи переменному току:

. (15)

Оно зависит от параметров цепи R,L и C и частоты тока .

Если рассматриваемый участок цепи представляет только конденсатор (R  0, L  0), то его сопротивление называется емкостным

. (16)

Сдвиг фаз при этом, как следует из (12), _C = -/2, т.е. напряжение на конденсаторе отстает от силы тока по фазе на /2, а по времени на 1/4 периода T.

Для участка цепи со значительным преобладанием индуктивности (R  0, 1/C  0) вводят индуктивное сопротивление

. (17)

В этом случае сдвиг фаз _L = +/2, т.е. на "чистой индуктивности" напряжение опережает ток по фазе на /2. Реальные катушки кроме индуктивного сопротивления L обладают еще и активным сопротивлением R_L – сопротивлением проволоки обмотки. Оно равно нулю только в сверхпроводящем состоянии металла. Поэтому сопротивление реальных катушек индуктивности переменному току

, (18)

а сдвиг фаз   .

Если участок цепи имеет пренебрежимо малые емкостное и индуктивное сопротивления ((1/С)  0, L  0), то

, (19)

и  = 0, т.е. полное сопротивление в этом случае равно только активному, а напряжение и ток по фазе совпадают.

В цепях с очень малым активным сопротивлением (R  0) полное сопротивление называют реактивным:

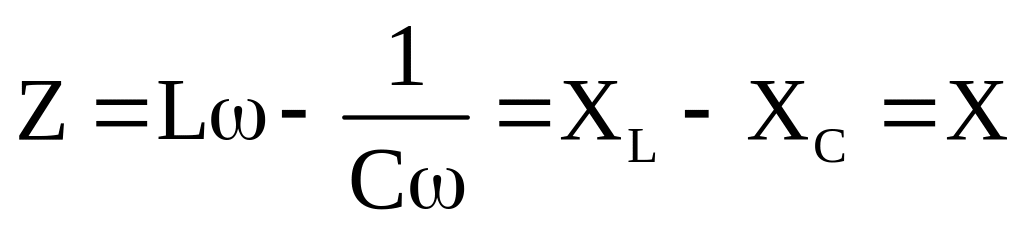. (20)

В такой цепи, сдвиг фаз между током и напряжением определяется соотношением между емкостным и индуктивным сопротивлением.