Работа №2

ИЗУЧЕНИЕ ЗАВИСИМОСТИ ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ МЕТАЛЛОВ И ПОЛУПРОВОДНИКОВ ОТ ТЕМПЕРАТУРЫ

Задание: изучить характер зависимости электрического сопротивления металлов и полупроводников от температуры; вычислить термические коэффициенты сопротивления металлов и ширину запрещенной зоны полупроводников.

Оборудование и принадлежности: установка для проведения измерений.

Описание установки

Установка предназначена для экспериментальной проверки зависимости омического сопротивления металла и полупроводника от температуры.

Металлическое сопротивление представляет собой тонкую проволоку, намотанную на картонный каркас. В качестве полупроводникового сопротивления использовано медно-марганцевое термосопротивление ММТ-12. Оба сопротивления помещены в пробирку, наполненную маслом. В эту же пробирку помещен термометр. Пробирку опускают в колбу с водой, подогреваемой электроплиткой.

С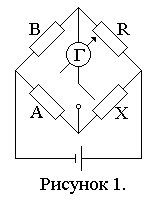 опротивление измеряется мостом постоянного тока типа МО. Этот мост представляет собой измерительный прибор, предназначенный для лабораторных измерений активных сопротивлений. Принципиальная схема приведена на рисунке 1. Она представляет собой цепь, состоящую из двух параллельно включенных ветвей. Каждая ветвь состоит из двух плеч (сопротивлений) А и В, R и X. В противоположные вершины моста включается источник питания и гальванометр-указатель равновесия моста. При равновесии моста ток через гальванометр не идет, и неизвестное сопротивление определяется по формуле X=AR/B, где R – отсчет по рычажному магазину ”плеча сопротивления” моста.

Изучение зависимости электрического сопротивления металлов и полупроводников от температуры

Теория электропроводности твердых тел при реальных температурах впервые была разработана П.Друде и Х.Лоренцом на основе представлений и понятий классической физики. Позднее были обнаружены явления, которые не могли быть объяснены в рамках классической теории Друде-Лоренца. С развитием квантовой физики было показано, что классическая статистика, использованная П.Друде и Х.Лоренцом, применима, например, к электронам в металлах лишь при определенных условиях. Для объяснения электропроводности твердых тел была разработана «зонная» теория, использующая представления и понятия квантовой физики.

1. Классические представления об электропроводности твердых тел

1.1. Электропроводность металлов

С точки зрения классической физики, током называется направленное движение заряженных частиц. Поэтому для протекания тока в твердых телах (проводниках) необходимо наличие свободных зарядов, т.е. заряженных частиц, которые могут перемещаться по всему объему вещества, а также наличие электрического поля, вызывающего их направленное движение.

Свободными зарядами (носителями тока) в твердых телах могут быть как электроны, так и ионы. В классической физике электроны – точечные отрицательно заряженные частицы, одинаковые для всех атомов и молекул. Поэтому говорят, что в случае электронной проводимости, ток не сопровождается переносом вещества.

К классу проводников относятся также многие соли, например NaCl, AgNO₃, NaNO₃, в которых свободными зарядами являются ионы. В этом случае, ток - направленное движение ионов, что сопровождается выделением вещества, как и при протекании тока в водных растворах этих солей. Поэтому эти соли называют твердыми электролитами.

С точки зрения классической физики, при образовании кристаллической решетки металлов освобождаются слабо связанные в атомах валентные электроны. Они являются свободными, и поэтому говорят, что проводимость металлов электронная.

В классической физике рассматривается определенная модель строения проводника с электронной проводимостью. Проводник – это нейтральная система из кристаллической решетки положительных ионов и хаотически движущихся между ними электронов. Электроны проводимости, двигаясь хаотически, «сталкиваются» с ионами решетки, в результате чего устанавливается тепловое равновесие между электронами и кристаллической решеткой. В некотором приближении электроны можно рассматривать как одноатомный электронный «газ» и соответственно рассчитать среднюю скорость их хаотического движения:

.

При температуре Т = 300 К эта скорость порядка 10⁵ м/с.

При наличии электрического поля в проводнике, электронный газ двигается направленно, причем электроны могут «сталкиваться» с ионами кристаллической решетки, «захватываться» ими, что характеризуется физическим понятием - удельное сопротивление вещества.

Удельное сопротивление  различных металлов при комнатной температуре имеет значение в пределах 10^-810^-6 Ом  м. Твердые вещества с большими значениями  (10¹⁰  10²⁰ Ом  м) называются диэлектриками (изоляторами). Вещества с промежуточными значениями  (10^-4  10¹⁰ Ом  м) называются полупроводниками. Это  ряд химических элементов (кремний, германий, селен, фосфор, мышьяк, теллур, йод и др.), большое количество различных соединений и сплавов, почти все неорганические вещества.

Рассмотрим, от чего зависит удельное сопротивление вещества с точки зрения классической физики. Для этого установим связь между силой тока в проводнике и параметрами проводника.

Пусть в некоторый момент времени проволочный проводник длиной ℓ, площадью поперечного сечения S и удельным сопротивлением  подключается к источнику постоянного напряжения U. В проводнике возникает постоянное электрическое поле с напряженностью Е, которое вызывает направленное движение электронов.

Для упрощения расчетов будем считать, что электрон движется ускоренно только под действием силы со стороны электрического поля. Тогда ускорение некоторого электрона можно рассчитать по второму закону Ньютона:

,

где e – заряд электрона, а модуль напряженности поля равен E = U/ℓ.

Пусть среднее время ускоренного движения или свободного пробега электронов между столкновениями <>. Следовательно, за время свободного пробега электрон приобретет скорость направленного движения =a<>.

При протекании тока через сечение проводника пройдет некоторый заряд q=Ne, где N – число прошедших через сечение проводника электронов.

N=nV=n<>tS, где n – концентрация свободных электронов в проводнике, V – объем электронного газа прошедшего через сечение проводника за время t, <>t – расстояние, пройденное электронами за это время, <> - средняя скорость направленного движения электронов.

Сила постоянного тока определяется зарядом, проходящим через поперечное сечение проводника за единицу времени:

.

Таким образом, сила тока в проводнике постоянного сечения определяется концентрацией электронов и средней скоростью их направленного движения.

В первом приближении можно считать, что при столкновении с ионом электрон полностью теряет свою энергию, т.е. его скорость становится равной нулю. Тогда среднюю скорость равноускоренного движения электронов в проводнике можно рассчитать по формуле

.

Следовательно

.

Сравним полученное выражение с установленным экспериментально законом Ома :

, где .

Сравнение полученного выражения для силы тока и закона Ома показывает, что удельное сопротивление равно

.

Следовательно, с классической точки зрения, удельное сопротивление различных проводников отличается потому, что они отличаются концентрацией свободных электронов и средним временем свободного пробега электронов.

Рассмотрим, от чего зависит последняя величина.

Расчеты показывают, что, для реальных проводников, средняя скорость направленного движения гораздо меньше скорости хаотического движения и является величиной порядка 10^-3 м/с.

Тогда, если не учитывать распределение электронов по скоростям при хаотическом движении, то приближенно можно считать, что время свободного пробега определяется средним расстоянием между узлами кристаллической решетки проводника <d> и средней скоростью хаотического движения <_X>:

, .

Таким образом, при рассмотренном классическом приближении, удельное сопротивление металлов зависит от концентрации свободных электронов, среднего расстояния между узлами кристаллической решетки и средней скорости хаотического движения электронов.

При повышении температуры концентрация свободных электронов в металлах не меняется, но увеличивается энергия теплового движения, как электронов, так и ионов кристаллической решетки. Скорость хаотического движения электронов при изменении температуры в реальном диапазоне 300К-350К существенно не изменяется. Но увеличение интенсивности колебательного движения ионов кристаллической решетки приводит к возрастанию величины удельного сопротивления при увеличении температуры.