3. Мощность, выделяемая на активном сопротивлении
Рассмотрим
задачу. Катушка с индуктивностью L
= 0,70 Гн и активным сопротивлением r
= 20 Ом соединена последовательно с
безындукционным сопротивлением R,
и между концами этой цепи приложено
переменное напряжение с действующим
значением U
= 220 В и частотой
= 314 с-1.
При каком значении сопротивления R
в цепи будет выделяться максимальная
Рисунок 10 – Последовательная цепь переменного тока с катушкой индуктивности: r – внутреннее сопротивление катушки
тепловая мощность? Чему она равна?
Когда в цепи отсутствует внешний источник, на основании второго закона Кирхгофа запишем
Приведем уравнение к стандартному виду
,
Его решение
,
Возьмем производную
,
Подставим в исходное уравнение
,
Отсюда коэффициент затухания
,
,
где
размерность
- с-1.
Рассмотрим вынужденные колебания в последовательной цепи c энергетической точки зрения с целью введения такого понятия как коэффициент мощности – cos . Итак, пусть теперь в цепи действует генератор.
Напряжение на конденсаторе и заряд конденсатора связаны соотношением
;
ток через конденсатор
.
Составим отношение
,
оно могло бы быть заменой закона Ома для конденсатора, но зависимость от времени делает это выражение бессмысленным
Однако, по аналогии с цепями постоянного тока можно ввести для амплитудных значений
,
где
.
Величина Xc может рассматриваться как сопротивление конденсатора. По крайней мере по размерности она совпадает с обычным сопротивлением.
Аналогично поступаем при рассмотрении индуктивности. Напряжение на катушке индуктивности
,
ХL – сопротивление катушки индуктивности.
Построение векторной диаграммы для последовательной цепи
Итак, для векторов колебаний напряжения имеем
,
Силу тока можем задавать с какой-то начальной фазой,, как на рис 11, а можем выбрать начальную фазу равной нулю:
Uc,m
Рисунок 11 – Векторы колебаний токов и напряжений в последовательной цепи переменного толка
Величину с радикалом уместно назвать полным сопротивлением цепи переменному току:
.
Примем
.
Итак, между током и напряжением в
последовательной цепи имеется сдвиг
фаз ,
такой что
Мощность. выделяемая в цепи:
Найдем среднее за период колебаний значение этой величины
.
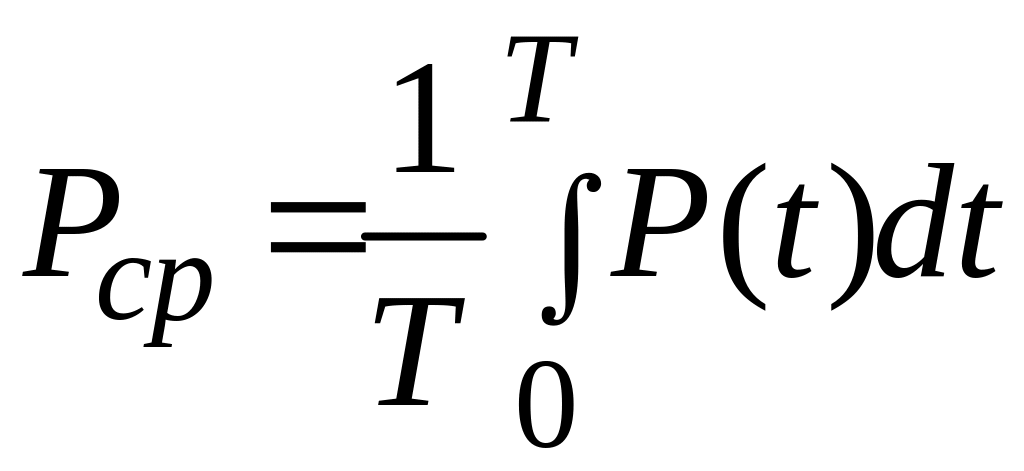
Действующие значения тока и напряжения принимаются равными
;
.
Итак, мощность, выделяемая на внешней нагрузке R:
,
где U и I – действующее напряжение и ток,
,
,
где Z – величина (модуль) так называемого комплексного (активного и реактивного) сопротивления цепи.
Итак, выделяемая мощность
.
Для нахождения максимума этой функции поступаем стандартным образом:
.
Имеем
.
Решая уравнение, имеем
,
.
При этом максимальная выделяемая мощность
.
Она не зависит от сопротивления катушки.