Департамент по авиации

Министерства транспорта и коммуникаций Республики Беларусь

Минский государственный высший авиационный колледж

Кафедра естественнонаучных дисциплин

Кафедра общетехнических дисциплин

Кириленко А.И., Сёмкина Н.И.

Методические указания

по выполнению курсовых работ

с вычислениями в табличном процессоре EXCEL

Минск - 2011

Департамент по авиации

Министерства транспорта и коммуникаций Республики Беларусь

Минский государственный высший авиационный колледж

Кафедра естественнонаучных дисциплин

КУРСОВАЯ РАБОТА (ПРОЕКТ)

ТЕМА:

По дисциплине

Специальность

курсанта (ФИО полностью)

курса группы

Руководитель /Ф.И.О./

Консультант /Ф.И.О./

Курсант /Ф.И.О./

Минск – 20__ г.

Департамент по авиации

Министерства транспорта и коммуникаций Республики Беларусь

Минский государственный высший авиационный колледж

УТВЕРЖДАЮ

Заведующий кафедрой ЕНД

___________Кириленко А.И.

«____» ___________20__ г.

ЗАДАНИЕ

на курсовую работу (проект)

по дисциплине ____________________________________________

курсанта______________ курса ________________________ группы

Фамилия, имя, отчество

Тема курсовой работы (проекта) _____________________________

При выполнении курсовой работы (проекта) по данной теме должны быть представлены:

1. Пояснительная записка (Введение)

2. Расчетно-графическая часть (В работе назвать конкретно)

3. Выводы

4. Список использованных источников

Руководитель курсовой работы (проекта) _________

подпись

Фамилия, имя, отчество

Консультант ___________________ _______________________

подпись Фамилия, имя, отчество

Дата выдачи ____ __________20__г.

Срок сдачи ____ __________20__г. Подпись курсанта __________

Минск- 20__ г

Оглавление

Введение……………………………………………………………..………...4

1. Последовательная электрическая цепь………………………………...….5

1.1. Свободные затухающие колебания в последовательной цепи……...5

1.2. Вынужденные электрические колебания……………………….…….6

2. Параллельная электрическая цепь……………………………………..…18

2.1. Затухающие колебания в параллельном контуре………..……..…...18

2.2. Вынужденные колебания в параллельном контуре………………...19

3. Мощность выделяемая на активном сопротивлении…………………..26

4. Зависимость напряжения на конденсаторе от индуктивности

контура ……………………………………………………………………….28

5. Вычисления и построение графиков в табличном процессоре Excel….. 29

5.1. Производство вычислений…………………………………………….29

5.2. Построение и оформление графиков…………………………………36

Выводы………………………………………………………………………...45

Список использованных источников………………………………………..46

Приложение 1………………… …………………………………………...47

Приложение 2………………… …………………………………………...50

Введение

Несмотря на разную природу колебаний, в них обнаруживаются одни и те же физические закономерности: колебания описываются одними и теми же уравнениями, исследуются общими методами, разработка и применение которых составляют задачу теории колебаний.

Причины возникновения колебаний могут быть различными. Наиболее распространен случай возникновения колебаний в результате нарушения устойчивости состояния равновесия. Как только система выводится из состояния равновесия, она будет совершать колебания относительно этого состояния. Вследствие неизбежных потерь энергии колебания постепенно затухают, и система возвращается к положению равновесия. Такие колебания называются свободными или собственными.

Колебания в системе могут возникать также в результате внешнего воздействия, имеющего колебательный характер. Такие колебания называются вынужденными. Они возникают в так называемых пассивных системах, то есть в системах, где отсутствуют источники энергии.

При рассмотрении колебаний надо учитывать, в каких системах они совершаются – линейных или нелинейных. Свойства линейных систем не меняются при изменении их состояния, то есть параметры линейной системы, характеризующие ее свойства (упругость, масса, коэффициент трения механической системы; емкость, индуктивность, сопротивление электрической системы), не зависят от величин, характеризующих состояние системы в процессе колебания (смещение и скорость в случае механической системы; напряжение и ток в случае электрической системы).

Линейные системы обладают свойствами, существенно упрощающими анализ происходящих в них процессов. Процессы в линейных системах описываются линейными дифференциальными уравнениями, в которых коэффициенты не зависят от переменных и их производных. Поэтому в линейных системах, во-первых, внешние воздействия, имеющие периодический характер, воспроизводятся без искажения формы, и, во-вторых, для линейных систем справедлив принцип суперпозиции (наложения): если на систему действуют две силы, создающие (каждая в отдельности) свое смещение, то при одновременном действии этих сил смещение равно сумме смещений.

Параметры реальных систем всегда в той или иной мере зависят от их состояния. Например, коэффициент упругости пружины зависит от величины деформации (то есть имеет место отклонение от закона Гука), активное сопротивление проводника зависит от его температуры, которая в свою очередь зависит от силы тока в проводнике и т.д.

Поэтому реальные системы можно рассматривать как линейные только в некоторых ограниченных пределах отклонения от состояния равновесия, при которых можно пренебречь изменением их параметров.

Введение заканчивается формулировкой цели и перечислением решаемых задач.

1. Последовательная электрическая цепь

1.1. Свободные затухающие колебания в последовательной цепи

Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают. Уравнение колебаний можно получить, исходя из того, что сумма падений напряжения на емкости, индуктивности и активном сопротивлении должна быть равна нулю [1]:

, (1)

где L – индуктивность катушки (Гн), [L] = кгм² с^-2А^-2; R – сопротивление резистора (Ом), [R] = кгм² с^-3А^-2; I – сила тока в цепи (А), С – емкость конденсатора (Ф), [C] =кг^-1м^-2 с⁴ А²; q – заряд на обкладках конденсатора (Кл), [q] = A  c.

Разделим это выражение на L и заменяя I через Q^/, а через q^//, получим:

.

Введем стандартные обозначения [2]:

, , (2)

где  - коэффициент затухания (с^-1); ₀ – собственная частота .

Последнее уравнение совпадает с дифференциальным уравнением затухающих механических колебаний. При условии, что   ₀, т.е. решение уравнения (1) имеет вид

, (3)

где - частота затухающих колебаний (с^-1), Q – начальная амплитуда заряда на конденсаторе (Кл) А.с, ₀ – начальная фаза колебаний (рад) - безразмерная величина, t + ₀ фаза - (рад) - безразмерная величина.

Таким образом, частота затухающих колебаний меньше собственной частоты ₀. При R = 0 получаем  = ₀.

График функции q(t) называется затухающей гармоникой (см. рис., например, в [3]).

Как видно из графика, заряд на конденсаторе убывает с течением времени. Для того чтобы поддерживать в последовательной цепи незатухающие колебания, необходим внешний источник энергии. Такие колебания называют вынужденными. Они создаются под действием генератора. Перейдем к их рассмотрению.

Не следует нумеровать все формулы подряд, а лишь только те, на которые в дальнейшем будут ссылки.

1.2. Вынужденные электрические колебания

В этом разделе будем использовать материал и стандартные обозначения физических величин из пособия И.В.Савельева, (Курс общей физики, §§ 90 - 91) [1].

Рассмотрим последовательную цепь переменного тока:

Рисунок 1 – Последовательная электрическая цепь переменного тока: U – напряжение на зажимах генератора (В); I – ток в цепи (А); С – конденсатор; L – катушка индуктивности; R – сопротивление (в конце подписи точка не ставится) Формулы в подписях под рисунками и над таблицами не размещать.

Зададим направление тока в этой цепи. Пусть генератор задает переменное напряжение (напряжением на зажимах )

,

где: - амплитуда напряжения на генераторе (В);  – частота генератора ( )

Из определения электроемкости следует:

, (3)

где: – напряжение на конденсаторе (В); q (t) – переменный заряд на пластинах конденсатора (Кл); С – емкость конденсатора (Ф).

Падение напряжения на резисторе:

На основании закона Ома падение напряжения на резисторе:

, (4)

где - напряжение на резисторе (В), I (t) – ток в цепи (А), R – сопротивление резистора (Ом).

Э Д С катушки индуктивности (В):

, (5)

где L – индуктивность катушки (Гн).

По второму закону Кирхгофа сумма падений напряжений в цепи равна:

, . (6)

Учтем, что по определению скорость изменения заряда – это ток:

.

Тогда

. (7)

Приведем уравнение (7) к стандартному виду, как это сделано в разделе 1.1:

,

где [q^// ] - Кл/с², [q]^/ - Кл/с ,

или

. (8)

Это уравнение колебаний, совершаемых под действием внешней гармонической силы. Поскольку в контур встроен внешний генератор, то колебания в контуре будут вынужденными, поскольку, те затухающие колебания, которые возбуждаются в контуре, спустя определенное время, прекращаются. Эксперимент показывает, что в этом случае колебания электрического заряда на конденсаторе происходят с той же частотой, что и частота генератора. Однако между напряжением на зажимах генератора и изменением заряда существует определенная разность фаз:

, (9)

где: Q - амплитуда колебания заряда на конденсаторе (Кл);  - разность фаз между напряжением на зажимах генератора и колебаниями заряда на обкладках конденсатора (рад).

Покажем, что решение (9) удовлетворяет уравнению (8) и найдем условия, при которых это справедливо.

Установившиеся колебания (9) по другому называются вынужденными, т.к. внешняя сила их «вынуждает».

Возьмем первую и вторую производную от выражения (9)

, (10)

, (11)

и подставим (9), (10) и (11) в (8):

,

- . (12)

Перенесем все члены (12) в левую часть и соберем коэффициенты при и . Они должны быть тождественно равны нулю, т.к. второй закон Кирхгофа справедлив в любой момент времени t, а и равны нулю не всегда: ,

. (13)

Эта система позволяет найти Q (амплитуду колебаний заряда) и сдвиг фаз . Из второго уравнения (13)

. (14) Формула (14) угол  определяет неоднозначно и для расчета через функцию тангенс необходимо выразить sin  и cos , и подобрать их знаки такими, чтоб удовлетворялась система (13).

Для нахождения амплитуды Q возведем первое уравнение в квадрат, а затем второе, и результаты сложим:

,

. (15)

Соотношения (14) и (15) показывают, что амплитуды и сдвиги фаз установившихся (вынужденных колебаний) зависят от частоты генератора. При этом, как видно из (14), сдвиг фаз  не зависит от амплитуды сигнала U₀. В то же время амплитуда установившихся колебаний прямо пропорциональна амплитуде сигнала. Сдвиг фаз зависит от характеристик колебательного контура и , и от частоты поступающего на контур сигнала . Амплитуда установившихся колебаний определяется как параметрами контура , так и амплитудой и частотой поступившего на контур сигнала. Итак, мы имеем следующие функции, описывающие установившиеся в контуре колебания. Эти зависимости можно выразить через параметры контура R, L, C.

Фаза  и амплитуда заряда – функций многих переменных

, .

Например, распишем (13) через и :

.

Те же самые преобразования производим с выражением (15), задавая R, L, C. Здесь мы можем построить семь графиков.

Определим закон колебания силы тока. В электротехнике принято все колебательные процессы приводить к одной фазе, поэтому необходимо синус заменить на косинус и убрать минус:

. (16)

Величину естественно назвать амплитудой тока .

Найдем напряжение на активном сопротивлении , на емкости и индуктивности .

. (17)

. (18)

, ,

. (19)

Итак, имеем

, ,

, .

Рассмотрим амплитуды напряжений на емкости, индуктивности и активном сопротивлении:

. (20)

. (21)

. (22)

.

Рассмотрим амплитуду напряжения на конденсаторе в зависимости от частоты:

. (23)

где функция задает резонансную кривую напряжения на конденсаторе, Эта кривая совпадает с кривой резонанса смещений.

.

На низких частотах   0 имеем:

. (24)

На высоких частотах    имеем:

U_C,m = 0. (25)

Выводы:

На низких частотах амплитуда напряжения на конденсаторе близка к амплитуде напряжения генератора. На высоких частотах напряжение на конденсаторе стремится к нулю.

Функция (см. рис. 2, табл. 1) при всех значениях  положительна, но вначале интервала принимает небольшое значение, а в конце превращается в нуль. Эта функция должна иметь максимум на некоторой частоте. Максимум функции соответствует той частоте, на которой знаменатель дроби (23) будет иметь минимум. Найдем минимум функции из (23):

.

Как видно, относительно ² это уравнение задает параболу, ветви которой направлены вверх, т.к. перед ⁴ стоит знак «+». Значит, функция имеет минимум, для его нахождения найдем производную и прировняем ее к нулю:

,

Имеем корни:

. (26)

. (27)

Напряжение, максимальное на конденсаторе, приходиться на частоту несколько меньше собственной частоты колебательного контура. Отметим, что все выкладки при рассмотрении вынужденных колебаний справедливы при условии:

₀  . (28)

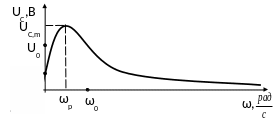
Рисунок 2 – Амплитуда напряжения на конденсаторе в зависимости от частоты генератора: ₀ - собственная частота контура; _р – резонансная частота; - амплитуда напряжения на генераторе Если кривая расчетная. то в подписи следует указать все параметры (начальные условия), при которых она построена: ₀; ; U _Cm; С; L; R и др.

При построении графика в Exel следует сопровождать его таблицей данных (которую можно размещать и в приложении) с обязательным указанием параметров (начальных условий), при которых этот график построен. Ссылка в тексте на рисунок, таблицу, литературу и приложение обязательна.

Найдем амплитуду натяжения на конденсаторе в резонансе: . (29)

При имеем:

. (30)

Кривая аналогична резонансной кривой смещения в механике.

Рассмотрим амплитуду напряжения на активном сопротивлении, она задается соотношением (20): . (31)

На низких частотах :

.

На высоких частотах :

.

Ищем максимум выражения :

.

Выпишем отдельно числитель и прировняем его к нулю:

,

,

,

т.е.

. (32)

Итак, резонанс напряжения на активном сопротивлении имеет место на собственной частоте контура. Найдем значение этого напряжения:

. (33)

Строим резонансную кривую.

Рисунок 3 – Амплитуда напряжения на активном сопротивлении в зависимости от частоты генератора: - амплитуда напряжения на генераторе; ₀ - собственная частота контура; _р – резонансная частота

Она аналогична резонансной кривой для резонанса скоростей в механике.

Найдем амплитуду напряжения на индуктивности:

, . (34)

Исследуем резонанс напряжения на индуктивности.

На низких частотах :

. (35)

На высоких частотах :

. (36)

Находим резонансную частоту:

, (37)

тогда:

. (38)

Согласно (38), резонансная частота колебаний напряжения на катушке индуктивности больше собственной частоты ₀.

Находим напряжение на катушке индуктивности на резонансной частоте:

. (39)

Строим функцию U _L,m () (рис. 4, табл.1)

Рисунок 4 – Амплитуда напряжения на катушке индуктивности в зависимости от частоты генератора: - амплитуда напряжения на генераторе; ₀ - собственная частота контура; _р – резонансная частота

Рисунок 5 – Векторная диаграмма напряжений (значений амплитуд и фаз) в последовательной цепи на резонансной частоте: U_R,m – вектор напряжения на активном сопротивлении (длина вектора равна амплитудному значению напряжения); U_L,m - вектор напряжения на индуктивности; U_C,m - вектор напряжения на емкости.

Связь между резонансными частотами, для резонанса напряжений на активном сопротивлении, индуктивности и емкости:

. (40)

Резонанс напряжений на индуктивности аналогичен резонансу ускорений в механических системах, график один и тот же [4].

, .

Рассмотрим фазовые соотношения и построим векторные диаграммы (рис. 5) [5].