Контрольные вопросы

1. Закон Ома в интегральной и дифференциальной формах. В каких единицах измеряется удельная электрическая проводимость?

2. Сопротивление, удельное сопротивление, зависимость удельного сопротивления от температуры.

3. Сделать вывод рабочих формул.

4. Изобразить две схемы измерения сопротивления, применяемые в лабораторной работе. В какой из этих схем измеряемое значение сопротивления не зависит от внутреннего сопротивления амперметра?

5. На рисунке представлена зависимость плотности тока j, протекающего в проводниках 1 и 2, от напряженности электрического поля Е. Найти отношение удельных электрических сопротивлений (удельных электропроводностей) материалов, из которых сделаны эти проводники.

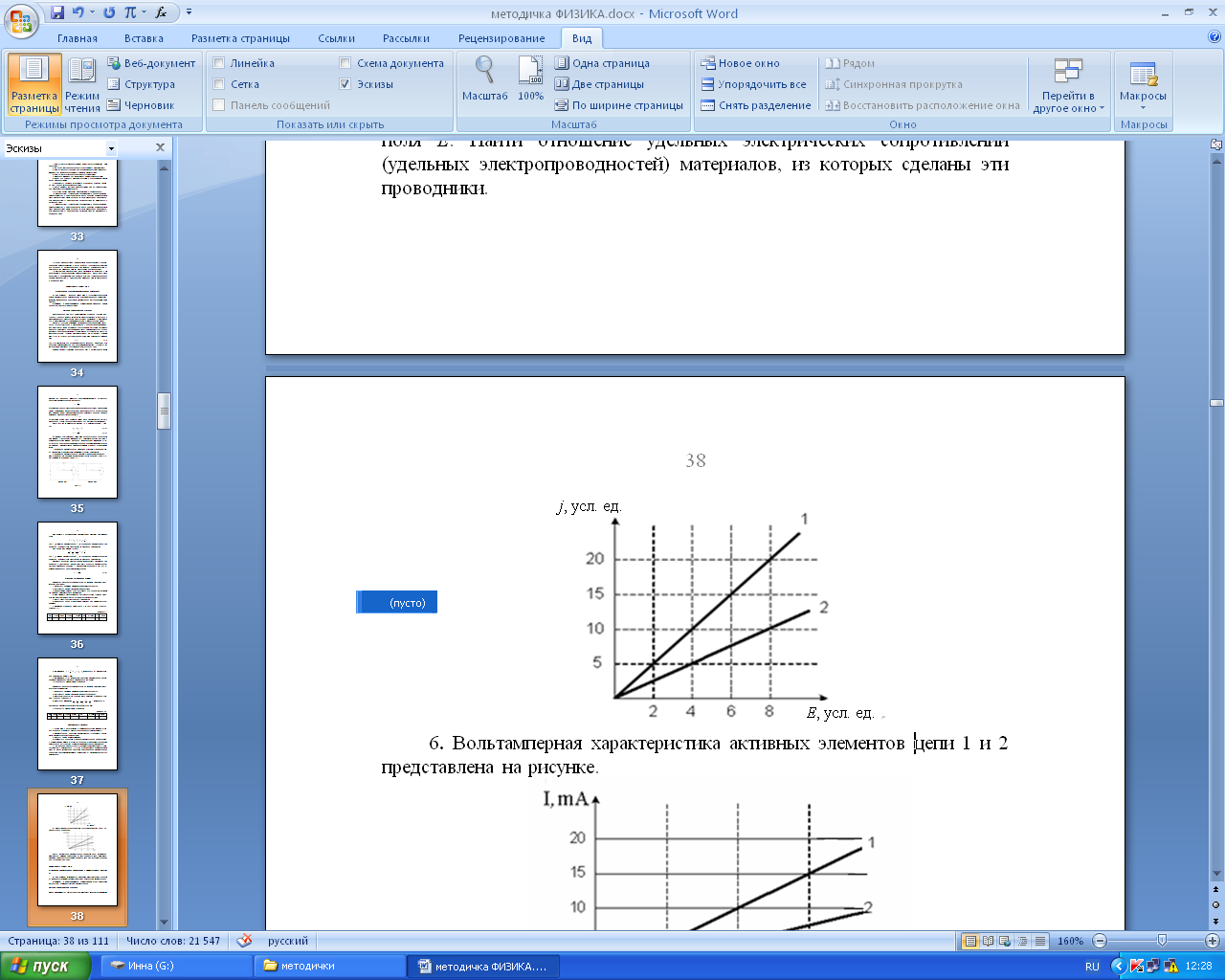
6. Вольтамперная характеристика активных элементов цепи 1 и 2 представлена на рисунке.

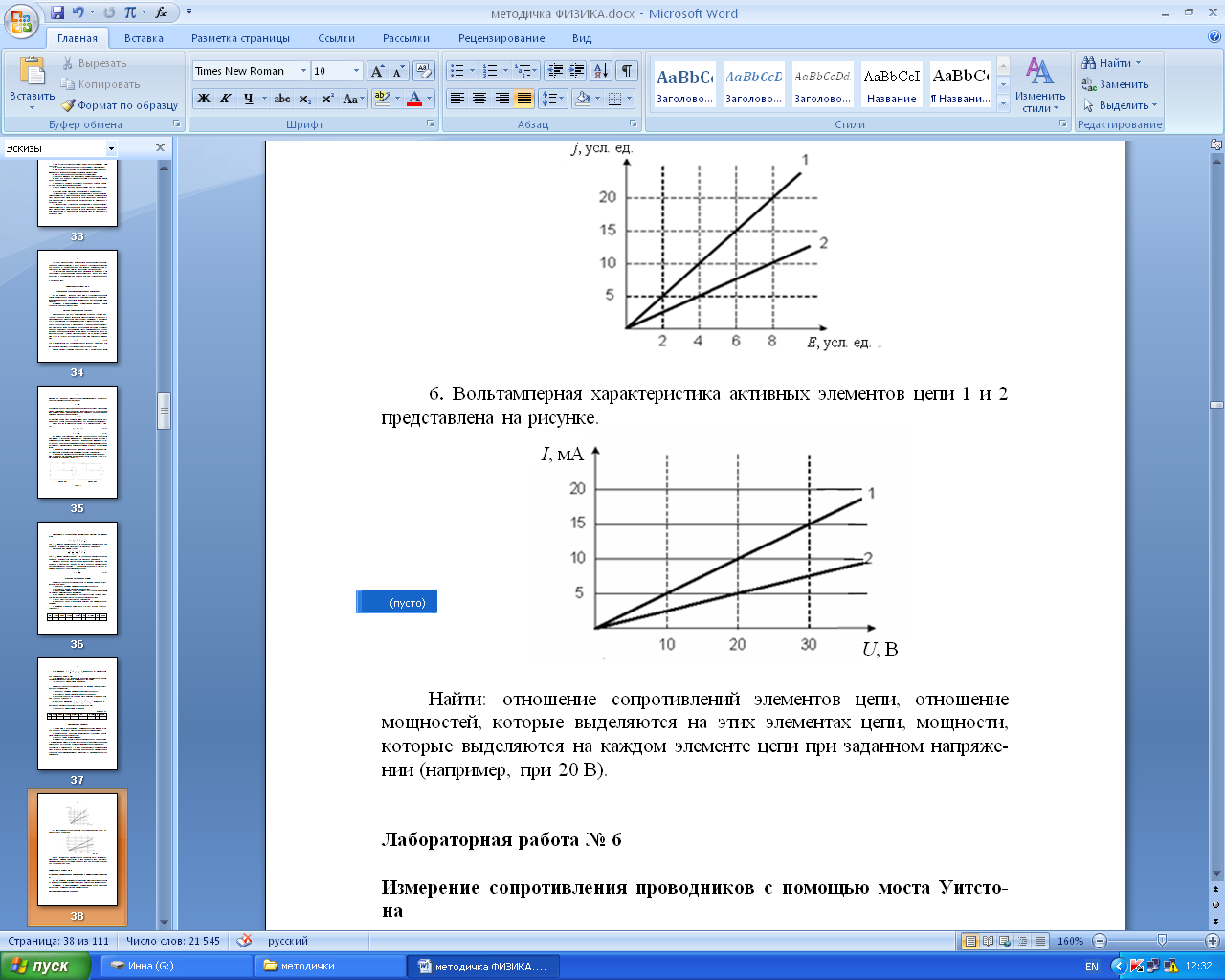
Найти: отношение сопротивлений элементов цепи, отношение мощностей, которые выделяются на этих элементах цепи, мощность, выделяющуюся на каждом элементе цепи при заданном напряжении (например, при 20 В).

Лабораторная работа № 6 измерение сопротивления проводников с помощью моста уитстона

Цель работы: ознакомиться со схемой моста Уитстона, научиться определять с помощью моста Уитстона неизвестные сопротивления.

Приборы и принадлежности: лабораторный стенд «Электромагнетизм», набор неизвестных сопротивлений.

Краткие теоретические сведения

Среди многообразия веществ металлы обладают наилучшей способностью проводить электрический ток. Это свойство получило название электропроводности. Из электронной теории металлов известно, что переносчиками зарядов в них являются свободные электроны, не связанные с узлами кристаллической решетки. Они представляют собой электронный газ, находящийся в постоянном тепловом движении. Под действием внешнего электрического поля движение электронов становится направленным, и они создают электрический ток. Плотность этого тока j зависит от напряженности внешнего электрического поля Е и удельной электропроводности проводника γ (в нашем случае – металла) j = γ·E.

При постоянном значении напряженности поля в различных металлах будет протекать ток различной плотности, которая в данном случае будет определяться различием удельных электропроводностей. Электропроводность металлов зависит от их природы, кристаллической структуры, наличия в ней дефектов кристаллического строения, присутствия примесей, а также от температуры. Максимальной электропроводностью будет обладать металлический проводник с идеальной кристаллической структурой, находящийся при температуре 0 К. В этом состоянии проводника ионы в узлах решетки не совершают тепловых колебаний и электроны не встречают препятствий на пути своего движения. При повышении температуры узлы кристаллической решетки приходят в постоянное тепловое движение, совершая беспорядочные тепловые колебания около положения равновесия. Поэтому в объеме металла временно возникают и исчезают области с большей или меньшей концентрацией ионов (в единице объема). Наличие таких флуктуаций плотности приводит к столкновению электронов с ионами (рассеянию электронов), что обуславливает уменьшение электропроводности.

Второй причиной уменьшения электропроводности является неидеальность структуры металлов. Возникающие при обработке металлов дефекты кристаллического строения, а также вводимые в металл примеси наряду с тепловыми колебаниями увеличивают неоднородность структуры и, следовательно, уменьшают электропроводность металлов.

Величина, обратная удельной электропроводности, называется удельным сопротивлением

ρ = 1/γ,

где ρ – удельное сопротивление, γ – удельная электропроводность.

Георгом Омом была установлена зависимость между током I, протекающим через проводник, и напряжением U:

.

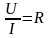Величину R, характеризующую данный проводник, Г. Ом назвал сопротивлением проводника. Сопротивление проводника зависит от его размеров, природы проводника и температуры:

R = ρ · l/S, ρ = ρ₀ (l + α t), (6.1)

где l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление, t – температура, α – температурный коэффициент сопротивления, ρ₀ – удельное сопротивление при t = 0 ºС.

Расчет сопротивления проводников по формулам (6.1) не всегда удобен. Поэтому для определения величины сопротивлений применяются различные методы. Одним из них является метод Уитстона.

М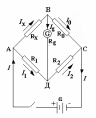 ост Уитстона представляет собой схему, применяемую для сравнения некоторого неизвестного сопротивления R_Х с известным сопротивлением R₀. Схема моста приведена на рис. 6.1.

Рис. 6.1

Четыре плеча моста Уитстона АВ, ВС, АД и ДС представляют собой сопротивления R_X, R₀, R₁ и R₂ соответственно. В диагональ ВД включается гальванометр, а в диагональ АС подсоединяется источник питания. В общем случае ток от источника ε будет протекать по всем участкам цепи, в том числе и через гальванометр G.

Однако, если соответствующим образом подобрать величины переменных сопротивлений R₁ и R₂, то можно добиться равенства потенциалов точек В и Д: φ_В = φ_Д. В этом случае ток через гальванометр не пойдет, то есть I_g = 0. При этих условиях мост будет сбалансирован, и можно приступить к расчету неизвестного сопротивления R_X. Для этого воспользуемся правилами Кирхгофа для разветвленных цепей. Применим первое правило Кирхгофа к узлам В и Д (рис. 6.1). Согласно этому правилу алгебраическая сумма токов, сходящихся в узле, равна нулю:

.

Токи, входящие в узел, будем считать положительными, а выходящие из него – отрицательными. Тогда для узла В можно записать:

I_X – I_g – I₀ = 0, (6.2)

а для узла Д:

I₁ + I_g – I₂ = 0. (6.3)

Учитывая, что для сбалансированного моста ток через гальванометр отсутствует, равенства (6.2) и (6.3) примут вид:

I_X = I₀ (узел В), I₁ = I₂ (узел Д). (6.4)

Второе правило Кирхгофа применим последовательно к контурам АВД и ВСД. Согласно этому правилу алгебраическая сумма э.д.с., действующих в контуре, равна алгебраической сумме произведений сил токов на соответствующие сопротивления:

Σε_i = ΣI_i·R_i.

Для контуров, не содержащих э.д.с., ΣI_i·R_i = 0.

Выберем за направление обхода контура направление по часовой стрелке. Токи, не совпадающие с этим направлением, берутся со знаком (–).

Учитывая вышеизложенное, для контура АВД запишем:

I_ХR_Х + I_gR_g – I₁R₁ = 0.

Соответственно для контура ВСД:

I₀R₀ – I₂R₂ – I_gR_g = 0.

Так как при сбалансированном мосте I_g = 0, то:

I_XR_X = I₁R₁,I₀R₀ = I₂R₂. (6.5)

Поделив почленно равенства (6.5) и учитывая полученные нами соотношения (6.4), получим:

R_X = R₀· R₁/R₂ (6.6)

В качестве известного сопротивления R₀ используется многодекадный магазин сопротивлений. Сопротивления R₁ и R₂ могут быть выполнены в виде однодекадных магазинов. Точность в определении R_X указанным методом в большой степени зависит от выбора сопротивлений R₁ и R₂. Наибольшая точность достигается при R₁ ≈ R₂.

В настоящей работе требуется:

1. Определить величину трех – пяти неизвестных сопротивлений R_xi.

2. Соединить измеренные сопротивления последовательно и определить величину полного сопротивления R_x΄. Полученную величину сравнить с рассчитанной по формуле:

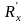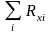= . (6.7)

3. Соединить измеренные сопротивления параллельно и определить величину полного сопротивления 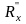. Полученную величину сопротивления сравнить с теоретически рассчитанной по формуле:

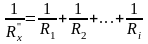(6.8)