Основные элементарные функции и их графики

Основными элементарными функциями называют следующие функции.

1. Показательная функция , . На рис. 4 показаны графики показательных функций, соответствующие различным основаниям степени.

Рис. 4.

2. Степенная функция , . Примеры графиков степенных функций, соответствующих различным показателям степени, представлены на рис. 5.

Рис. 5

3. Логарифмическая функция , . Графики логарифмической функции, соответствующие различным основаниям, показаны на рисунке 6.

Рис. 6

4. Тригонометрические функции , , , . Графики тригонометрических функций имеют вид, показанный на рисунке 7.

Рис. 7.

5. Обратные тригонометрические функции , , , . На рис. 8 показаны графики обратных тригонометрических функций.

Рис. 8.

Занятие 2 преобразование графиков функций. Сдвиг графиков поосям координат. Симметрия графиков относительно осей координат, начала координат. Основные правила. Примеры. Параллельный перенос

1. Перенос вдоль оси ординат f(x) f(x)-b

Для построения графика функции следует построить график функции и перенести ось абсцисс на единиц вверх при или на единиц вниз при . Полученный в новой системе координат график является графиком функции .

Пример 1. Построить график функции

Р е ш е н и е. Запишем функцию в виде . Строим график функции в координатах . Переносим ось на 3 единицы вниз. В координатах получаем

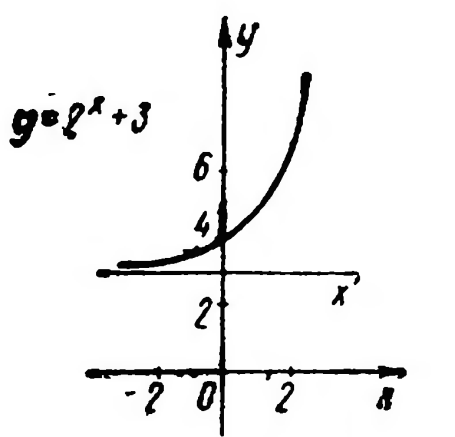
Рис. 9

график функции (рис.9). Прямая у=3 является горизонтальной асимптотой. График пересекает ось ординат в точке у=4.

2. Перенос вдоль оси абсцисс f(x) f(x+a)

Для построения графика функции следует построить график функции и перенести ось ординат на единиц вверх при или на единиц вниз при . Полученный в новой системе координат график является графиком функции .

Пример 2. Построить график функции

Рис. 10

Отражение

1. Построение графика функции вида y=f(-x); f(x) f(-x)

Для построения графика функции y=f(-x) следует построить график функции y=f(x) и отразить его относительно оси ординат.

Пример 3. Построить график функции .

Решение. Строим график функции (рис. 11 –пунктирная линия) и отражением его относительно оси ординат получаем график функции

Пример 4. Построить график функции y=arcos(-x).

Решение. Строим график функции y=arccos(x) (рис. 12 –пунктирная линия) и отражением его относительно оси ординат получаем график функции y=arcos(-x).

Рис. 11 Рис. 12

2. Построение графика функции вида ;

Для построения графика функции следует построить график функции y=f(x) и отразить его относительно оси абсцисс.

Пример 5. Построить график функции .

Решение. Строим график функции y=cos(x). (рис.13 – пунктирная линия) и отражением его относительно оси абсцисс получаем график функции y=-cosx.

Пример 6. Построить график функции

Решение. Строим график функции (рис.14 – пунктирная линия) и отражением его относительно оси абсцисс получаем график функции

Рис.13 Рис. 14

3. Построение графиков четной и нечетной функций

Для построения графика четной функции y=f(x) следует построить ветвь графика этой функции только в области положительных значений аргумента х ≥ 0. График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно оси ординат и получается отражением ее относительно этой оси.

Пример 7. Построить график функции .

Решение. Исходная функция является четной, поэтому строим график функции в области положительных значений аргумента х ≥ 0, где она имеет вид y=tgx. Левую ветвь графика получаем отражением относительно оси ординат (рис. 15).

Пример 8. Построить график функции .

Решение. Данная функция – четная, поэтому достаточно построить ее график лишь в области положительных значений аргумента х > 0 . График исходной функции в области отрицательных значений х получаем отражением относительно ординат (рис. 16).

Рис. 15 Рис. 16

Для построения графика нечетной функции y=f(x) следует строить ветвь графика этой функции только в области положительных значений аргумента х ≥ 0. График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат и может быть получен отражением этой ветви относительно оси ординат с последующим отражением в области отрицательных значений х относительно оси абсцисс.

Пример 9. Построить график функции

Решение. Исходная функция является нечетной, поэтому строим график функции в области положительных значений аргумента х ≥ 0, где она имеет вид .

Левую ветвь графика получаем отражением построенной ветви относительно начало координат (рис. 17)

Пример 10. Построить график функции

Решение. Данная функция является нечетной, поэтому строим ее график лишь в области х > 0 (точка х=0 не входит в область определения функции), где она имеет вид у=1. Левую ветвь графика получаем отражением построенной ветви относительно начало координат. На рисунке 18 стрелки означают, что точки х=0, у=1 и х=0, у=-1 не принадлежать графику.

Рис. 17 Рис. 18

4. Построение графика обратной функции

Для построения графика функции , обратной по отношению к функции , следует построить график и отразить его относительно прямой .

Пример 10. Построить график функции .

Решение. Рассмотрим график параболы у=х² (Рис. 19—пунктирная кривая) и график обратной к ней функции , получаемой отражением параболы относительно прямой у=х.

Пример 11. Построить график функции .

Решение. Данная функция является обратной по отношению к функции у=х³, поэтому строим график функции у=х³ и отражением его относительно прямой у=х (рис. 20).

Рис. 19 Рис. 20