Примеры решения задач.
1.Решить уравнение
а)
.
Решение:
Воспользуемся геометрическим смыслом модуля: решением уравнения будут являться точки х такие, что расстояние от точки х до точки смены знака модуля (точки х=3) равно 5.
Ответ: х=-2; х=8.
б) Решить уравнение
.
Решение:
Построим графики
функций у=
и
у=3.
Найдем абсциссы их точек пересечения: х=-1 и х=5.
Ответ: х=-1 и х=5.
2. Решить уравнение
.
Решение:
На расстоянии 4 от точки х на координатной прямой лежат две точки: -1 и 7, а 2х есть одна из них.
Следовательно, 2х=-1
или 2х=7, так что заданное уравнение имеет
2 корня:
и
.
Также можно было,
разделив обе части уравнения на 2,
получить уравнение вида
.
И воспользоваться геометрическим
смыслом модуля: решением уравнения
являются точки х такие, что расстояние
от точек х до точки смены знака модуля
(точки х=
)
равно 2.
Ответ: х= , х= .
3. Решить неравенство
.
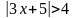Решение:
Разделим обе
части неравенства на 3 и перейдем к
равносильному неравенству
,
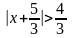геометрический смысл которого состоит
в нахождении точек х, расстояния от
которых до точки
больше
чем
.
Ответ:
.
4. Решить
уравнение
.
Решение:
На равном
расстоянии от точек -6 и 2 лежит единственная
точка- середина отрезка
,
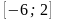т.е. х=-2. Это и есть единственный корень
данного уравнения.
Ответ: х=-2.
5.
Решить уравнение
.
Решение:
.
Ответ: х=2.
6. Решить уравнение
.
Решение:
1. Вычислим нули подмодульных выражений:
;
;
;
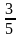
Ответ: .
7. Решите уравнение
,
выбрав наиболее рациональную схему для
решения :
1.
2.
Решение:
Вторая схема проще т. к. предполагает решение линейного неравенства, в отличие от первой, где пришлось бы решить два квадратных неравенства.
2)
Ответ: -3;-2;0.
Решите уравнение:
Решение:
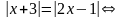
Ответ:
.
Решите уравнение
Решение:
Ответ:
.
10.
Решение:
x=9
Ответ: x=9
Решите уравнение
.
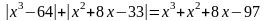Решение:
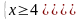
Ответ: .
12. Решите
неравенство
.
Решение:
(х
-5х+9)
<(х-6)
(х
-5х+9)
-(
х-6)
<0
(х -6х+15)( х -4х+3)<0 х -4х+3<0 1<x<3.
Ответ: (1;3).
Решить неравенство:
.
Решение:
.
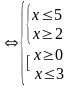
Ответ:
Задачи для работы в аудитории Уравнения и неравенства с модулем.
Устно: раскройте модули:
а)
;
б)
;
в)
;
г)
;
д)
.
1.Упростите выражение:
а)
,
если
;
б)
;
в)
;
г)
;
д)
;
е)
.
2.Решить простейшие уравнения и неравенства с помощью геометрической интерпретации модуля:
а)
;
б)
;
в)
;
г)
.
3. Отметить на координатной прямой множество всех точек х, удовлетворяющих данному условию, и записать его с помощью уравнения и неравенства с модулем:
а) расстояние от точки х до точки -3 больше 4;
б) сумма расстояний от точки х до точек 3 и 8 больше 4;
в) расстояния от точки х до точек с координатами 8 и 12 равны.
Способ раскрытия модуля.
|
4. Решить уравнения способом раскрытия модуля.
а)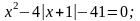
б)
;
в)
;
г)
.
Уравнения вида |
5.Решить уравнения
а)
;
б)
.
Уравнения вида
|
6.Найти корни уравнения
а)
;
б)
.
7*. Решите уравнения
8*. Решите уравнения
9. Используя график функции решите уравнения :
а)
;
б)
;в)
.
10*. Постройте
график функции
и решите уравнение:
а) =6; б) =5; в) =2; г) =0.
Неравенства с модулем
Неравенства вида |
11.Решить неравенство:
а)
;
б)
.
Неравенства вида |
12. Решить неравенство:
а)
;
б)
;
в)
.
Неравенства вида |