2.2 Понятие об измерении. Виды измерений. Приближенные вычисления

Величиной назовем то, что может быть измерено. Важнейшее назначение чисел – измерять величины, служить мерой сравнения их значений. Например, с помощью числа можно измерить следующие величины: длину, объем, скорость прямолинейного движения, температуру, энергию, производительность труда, стоимость продукции, национальный доход и пр.

В расчетах и вычислениях используют числа двух видов: точные и приближенные. Точные числа, как правило, получаются в результате натурального счета.

Приближенные – это числа, незначительно отличающиеся от точных и используемые в вычислениях вместо них. Приближенные числа получаются в результате измерений или вычислений.

Измерения могут быть непосредственные (например, с помощью приборов) и косвенные. Например, массу большого тела можно вычислить по формуле m=ρ*V, где ρ – плотность вещества, V – объем тела. Любой измерительный прибор имеет ограниченную область применения и точность измерения, при использовании косвенных методов измерения возникают специфические источники неточностей. Например, определение массы тела по плотности вещества зависит от наших знаний степени однородности тела по его объему. Или при определении площади фигуры неправильной формы методом взвешивания используется предположение о том, что толщина бумаги и плотность бумажной массы в любом месте фигуры одинаковы.

Математическими характеристиками точности приближенных чисел являются абсолютная и относительная погрешности.

Пусть а – точное, вообще говоря неизвестное числовое значение некоторой величины, а а* - известное приближенное значение этой величины, тогда величину

(а*) = | а – а*| называют абсолютной погрешностью числа а*, а величину (а*) = – его относительной погрешностью. Так как точные значения величин обычно бывают неизвестны, поэтому и погрешности, как правило, оценивают

Пример. В качестве приближенного значения √3 взяли число 1,7. Оценить погрешность приближения.

Решение.

Так как 1,7²=2,89<3, а 1,8²=3,24>3, то 1,7<√3<1,8, поэтому | √3-1,7|<0,1, то есть абсолютная погрешность приближения не превосходит 0,1. Относительная погрешность не превосходит величину Значение погрешностей в данном случае можно оценить и точнее.

Когда говорят о точности вычисления, например, что вычисления ведутся с точностью до десятых или сотых, имеют в виду, что абсолютная погрешность вычислений не превосходит единицы последнего сохраненного разряда (соответственно десятых или сотых)

На практике используют следующие правила расчета погрешностей.

1. Абсолютная погрешность суммы приближенных чисел равна сумме абсолютных погрешностей слагаемых.

2. Абсолютная погрешность разности приближенных чисел равна сумме абсолютных погрешностей слагаемых.

3. Относительная погрешность произведения приближенных чисел равна сумме относительных погрешностей множителей.

4. Относительная погрешность частного приближенных чисел равна сумме относительных погрешностей делимого и делителя.

Совершенно очевидно, что при большом количестве действий такие правила нельзя считать удовлетворительными, так как погрешности будут иметь разные знаки и компенсировать друг друга. При любых расчетах надо устанавливать такую точность вычислений, чтобы погрешность округления была существенно меньше всех остальных погрешностей.

Существуют четыре источника погрешностей, возникающих в результате численного решения задачи.

1. Математическая модель. Погрешность математической модели связана с ее приближенным описанием реального объекта. Например, если при моделировании экономической системы не учитывать инфляции, а считать цены постоянными, трудно рассчитывать на достоверность результатов. Погрешность математической модели называется неустранимой. Будем в дальнейшем предполагать, что математическая модель фиксирована и ее погрешность учитывать не будем.

2. Исходные данные. Исходные данные, как правило, содержат погрешности, так как они либо неточно измерены, либо являются результатом решения некоторых вспомогательных задач. Например, производительность оборудования, предполагаемая цена товара и др. Во многих физических и технических задачах погрешность измерений составляет 1 – 10%. Погрешность исходных данных так же, как и погрешность математической модели, считается неустранимой и в дальнейшем учитываться не будет.

3. Метод вычислений. Применяемые для решения задачи методы как правило являются приближенными. Например, заменяют интеграл суммой, функцию – многочленом, производную – разностью и т. д. Погрешность метода необходимо определять для конкретного метода. Обычно ее можно оценить и проконтролировать. Следует выбирать погрешность метода так, чтобы она была не более, чем на порядок меньше неустранимой погрешности. Большая погрешность снижает точность решения, а меньшая требует значительного увеличения объема вычислений.

4. Округление в вычислениях. Погрешность округления возникает из-за того, что вычисления производятся с конечным числом значащих цифр (для ПК это 10 – 12 знаков). Округление производят по следующему правилу: если в старшем из отбрасываемых разрядов стоит цифра меньше пяти, то содержимое сохраняемых разрядов не изменяется; в противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. При решении больших задач производятся миллиарды вычислений, но так как погрешности имеют разные знаки, то они частично взаимокомпенсируются.

Проиллюстрируем сказанное. Пусть имеется реальный маятник, совершающий затухающие колебания, начинающий движение в момент t = t₀. Требуется найти угол отклонения φ от вертикали в момент t₁. Движение маятника мы можем описать следующим дифференциальным уравнением:

,

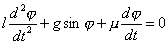где l – длина маятника, g – ускорение силы тяжести, μ – коэффициент трения.

Как только принимается такое описание задачи, решение уже приобретает неустранимую погрешность, в частности потому, что реальное трение зависит от скорости не совсем линейно (погрешность модели). Кроме того, воспроизведя реальный эксперимент, мы зададим l, g (в известной точке планеты), μ с некоторой точностью, и получим набор значений с погрешностью, которую можем оценить из анализа статистики некоторого числа однотипных опытов (погрешность исходных данных). Взятое в модели дифференциальное уравнение нельзя решить в явном виде, для его решения требуется применить какой-либо численный метод, имеющий заранее известную погрешность, которая должна быть меньше неустранимой погрешности. После совершения вычислений мы получим значения с погрешностью большей, нежели погрешность метода, так как к ней прибавится погрешность округления.