Биномиальное распределение Формула Бернулли

Пусть производится n независимых друг от друга испытаний, в каждом из которых случайное событие А может либо произойти, либо не произойти. Результат каждого испытания — случайное событие, вероятность которого естественно счи­тать независящей от результатов других бросаний. Вероятность того, что событие А состоится в каждом испытании одна и та же и равна p. Следовательно, вероятность того, что событие А не произойдет, равна 1–р. Обозначим эту величину через q=1–р. Зададимся вопросом, какова будет вероятность того, что при n испытаниях событие А наступит в k из них и, соответственно, в n-k испытаниях не наступит?

Для подсчета вероятности пронумеруем испытания. Для начала найдем вероятность наступления события А в испытаниях с определенными k номерами, и ненаступления в остальных n-k испытаниях. Так как испытания независимы, то по теореме умножения вероятностей получим вероятность такого сложного события равной . Наше искомое событие, состоящее в наступлении А в любых k испытаниях из общего числа n испытаний, разбивается на вышеупомянутые сложные несовместные события, количество которых . Например, если n=4, а k=2, то такие события: AA , А А , А А, A А, АА, АА . В этих записях А обозначает наступление события, а - ненаступление. Так AA означает, что интересующее нас событие наступило в 1 и 2 испытании, а в 3 и 4 – не наступило.

По теореме сложения вероятностей для несовместных событий вероятность наступления события А в k из n испытаниях (сумма одинаковых слагаемых, каждое из которых равно ).

Таким образом, (0£ k£ n). (5.7)

Полученная формула носит название формулы Бернулли.

Ясно, что несовместные сложные события, состоящие в появлении события А 0 раз, 1 раз, 2 раза, …, n раз в n испытаниях образуют полную группу событий. Поэтому сумма вероятностей этих событий для 0£ k£ n равна единице: .

Это соотношение можно получить, непосредственно вычислив сумму , применив формулу бинома Ньютона ( ):

= = = =1.

Пример 29. Построить ряд распределения числа выпавших гербов при двух бросках монеты.

Случайная величина – количество выпавших гербов при двух подбрасываниях монеты, в отличие от примера 6.1, может принимать три значения: 0, 1 и 2. Значение =0 соответствует тому, что герб не выпал ни разу, значение =1 соответствует выпадению герба и решки или решки и герба, значение =2 – выпадению двух гербов. Соответствующие вероятности можно найти по формуле Бернулли, но еще легче по теоремам умножения и сложения вероятностей: ; ; . .

Ряд распределения запишется в виде:

X	0	1	2
p

Пример 30. Стрелок производит три выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,6. Построить ряд и многоугольник распределения числа попаданий в мишень.

Случайная величина Х – число попаданий в мишень при трех выстрелах. Возможные значения Х: =0, =1, =2, =3. Вероятность того, что произойдут k попаданий (k=0, 1, 2, 3) при трех выстрелах подсчитывается по формуле Бернулли (5.7):

(0£ k£ 3),

где вероятность попадания при одном выстреле p=0,6 , q - вероятность промаха, q=1–0,6=0,4.

= = =0,064;

= = =3 =0,288;

= = =3 =0,432;

= = =0,216.

Ряд распределения случайной величины Х имеет вид:

X	0	1	2	3
p	0,064	0,288	0,432	0,216

Можно проверить, что, действительно, =0,064+0,288+0,432+ +0,216=1.

Многоугольник распределения числа попаданий при трех выстрелах изображен на рис.5.3.

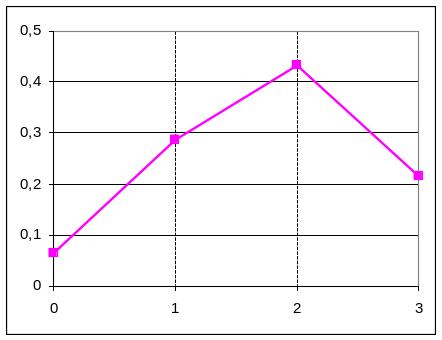
Рис. 5.3

Распределения случайных величин в примерах 6.3 и 6.4 являются частными случаями биномиального распределения вероятностей при n=2 и n=3.

Биномиальным называется распределение вероятностей, определяемое формулой Бернулли:

(0£ k£ n). (6.1)

Формула (6.1) является аналитическим выражением биномиального закона распределения.

По биномиальному закону распределена случайная величина Х числа появлений события А при проведении n независимых испытаний, если вероятность появления события А в каждом испытании одинакова и равна p (q=1–p). В n испытаниях событие А может вообще не появиться, появиться 1 раз, 2 раза, 3 раза, …, n раз. Таким образом, возможные значения Х таковы: =0, =1, =2, =3, …, =n. А соответствующие им вероятности подсчитываются по формуле Бернулли (6.1). Ряд распределения в этом случае будет таким:

X	0	1	2	…	k	…
p				…		…

Cумма вероятностей, соответствующих возможным значениям случайной величины, записывается в виде бинома Ньютона:

+ + +…+ +…+ = = . (6.2)

Естественно, что в формуле (6.2) p+q=1 и поэтому =1.