3.2. Основные операции над множествами Равенство множеств

Множества А и В считаются равными, если они состоят из одних и тех же элементов.

Равенство множеств обозначают так: А=В.

Если множества не равны, то пишут А В.

Запись равенства двух множеств А=В эквивалентна записи А В, или В А.

Например, множество решений уравнения х2-5х+6=0 содержит те же самые элементы, что и множество простых чисел, меньших пяти. Эти два множества равны.

Пересечение (умножение) множеств

Множество D, состоящее из всех элементов, принадлежащих и множеству А и множеству В, называется пересечением множеств А и В и обозначается D=А В (рис.3.1).

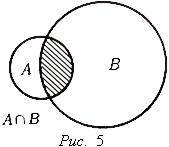
Рис.3.1

Рассмотрим два множества: Х= 0,1,3,5 и Y= 1,2,3, 4 . Числа 1 и 3 только они принадлежат одновременно обоим множествам Х и Y. Составленное из них множество 1,3 содержит все общие для множества Х и Y элементы. Таким образом, множество 1,3 является пересечением рассмотренных множеств Х и Y:

1,3 = 0,1,3,5 1,2,3, 4 .

Для отрезка и интервала(0;3) пересечением является промежуток (0;1 .

Пересечением множества прямоугольников и множества ромбов является множество квадратов.

Пересечение множества учеников восьмых классов данной школы и множества членов химического кружка той же школы есть множество учеников восьмых классов, являющихся чле­нами химического кружка.

Пересечение множеств (и другие операции — см. ниже) хо­рошо иллюстрируется при наглядном изображении множеств на плоскости. Для наглядного представления соотношений между несколькими подмножествами какого-либо универсума Венн предложил использовать круги и прямоугольники. При этом универ­сум представляется множеством всех точек некоторого прямо­угольника, а его подмножества — соответствующими кругами. В дальнейшем такие схемы стали называть диаграммами Эйлера-Венна.

Если множества А и В не имеют общих элементов, то гово­рят, что эти множества не пересекаются или что их пересече­ние — пустое множество, и пишут А В = .

Например, пересечение множества четных чисел с множе­ством нечетных чисел пусто.

Пересечение любого множества А с пустым множеством есть, очевидно, пустое множество: А = .

Можно рассматривать пересечение п множеств:

Аi=A1 A2 … An при этом в А входят только те элементы, которые входят во все множества А1, А2, ... Аn .

Например, если A, В и С — соответственно множества уче­ников класса, решивших на контрольной по математике задачу по алгебре, задачу по геометрии, задачу по тригонометрии, то пересечение этих множеств есть множество учеников этого клас­са, решивших все три задачи.

Объединение (сумма) множеств

Объединением множеств А и В называется такое множество С, каждый элемент которого содержится хотя бы в одном из множеств А или В: С = А В (рис.3. 2).

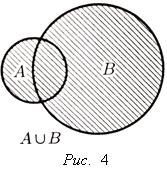
Рис 3.2.

Объединением множества учеников школы моложе 12 лет с множеством учеников той же школы старше 10 лет является множество всех учеников данной школы.

Можно рассматривать объединение п множеств: Аi=A1 A2 … An, при этом в А входят все элементы, которые входят хотя бы в одно из множеств А1, А2, ... Ап.

Например, множество всех действительных чисел R состо­ит из множества положительных чисел R+, множества отрица­тельных чисел R- и множества {0}, т. е.:

R = R+ R- {0}

Объединение множеств вершин треугольников, вписанных в данную окружность, представляет собой множество точек этой окружности.

Пример 2.

Пусть Е — некоторый универсум, а множество А принад­лежит этому универсуму, т. е. А с Е.

Записать и изобразить с помощью диаграмм Эйлера-Венна пересечение и объединение этих множеств.

Решение.

Универсум Е изобразим в виде прямоугольника, а его под­множество А — в виде круга, расположенного внутри прямо­угольника.

Чтобы найти пересечение двух множеств, можно исполь­зовать следующий способ: территорию одного множества за­штриховать, например, вертикальной штриховкой (пусть в дан­ном случае это будет множество Е), а территорию другого множе­ства — горизонтальной штриховкой (пусть в данном случае это будет множество А). Та территория, где штриховки наложились друг на друга, и будет представлять пересечение двух множеств.

Для случая рассматриваемой задачи пересечением будет являться территория множества А (рис.3.3), или просто мно­жество А: А Е = А, так как именно там штриховки наклады­ваются друг на друга.

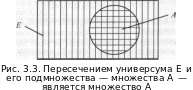
Чтобы найти объединение множеств, можно использовать следующий способ: территорию одного множества заштрихо­вать, например, горизонтальной штриховкой и территорию дру­гого множества также заштриховать горизонтальной штрихов­кой. Вся заштрихованная территория будет представлять собой объединение множеств.

Д ля случая рассматриваемых множеств объединением бу­дет являться территория множества Е (рис. 3.4), или просто множество Е: А Е = Е, так как именно территория универсу­ма — множества Е — оказывается полностью заштрихованной.