Прилади та обладнання:

5. комплект моделей плоских механізмів типу ТММ-5M;

6. моделі механізмів;

7. вимірювальні та креслярські інструменти;

Порядок виконання роботи

1. Ознайомитися з умовними позначеннями, що використовуються для

зображення кінематичних схем – заповнити таблицю 3.1 технологічного звіту;

2. Ознайомитися з роботою механізмів виданих викладачем. З’ясувати

характер руху ланок, а також, які кінематичні пари утворюють ланки між собою (обертальні, поступальні чи вищі);

3. Накреслити кінематичну схему механізму у відповідності з умовними

позначеннями згідно ГОСТ 2.770-68. Виміряти відстань між центрами

кінематичних пар,які обертаються,відстань на яку переміщується ланка

поступальної пари, число зубів зубчатих коліс, діаметри шківів і т.д. ці розміри проставити на схемі механізму. Підрахувати кількість ланок і кінематичних пар. Отримані данні занести в звіт.

4. Позначити ланки і кінематичні пари. Ланки рекомендується позначати арабськими цифрами, розпочинаючи від ведучої, а кінематичні пари латинськими великими літерами.

Звіт (додається)

Контрольні питання:

1. Що називається деталлю, ланкою?

2. Що називається кінематичною парою? Класифікація кінематичних пар.

3. Що називається кінематичним ланцюгом та механізмом?

4. Які механізми називаються плоскими і які просторовими?

5. Написати формулу для визначення ступеня рухомості плоских та просторових механізмів. Навести приклади.

Технологічний звіт Складання кінематичних схем механізмів

1. Мета роботи: засвоїти методику складання кінематичних схем механізмів з використанням стандартних умовних по значень.

2. Прилади та обладнання:

1. комплект моделей плоских механізмів типу ТММ-5M;

2. моделі механізмів;

3. вимірювальні та креслярські інструменти;

3. Проведення досліду

3.1 Таблиця 3.1 Умовні позначення в схемах елементів кінематики по ГОСТ 2.770-68

№ п/п	Найменування	Позначення

3.2 Кінематична схема механізму, числові значення розмірів ланок

3.3 Характеристика кінематичних пар

І Н С Т Р У К Ц І Й Н А К А Р Т А

для проведення лабораторної роботи № 7 з теми

«Визначення параметрів зубчастих коліс»

Мета роботи: ознайомитися з основними елементами і геометрією зубчастих коліс; навчитися визначати основні параметри циліндричного прямозубого стандартного колеса з евольвентним профілем зуба.

Визначення параметрів зубчастих коліс за результатами обмірювання їх зразків виконується з метою відновлення або виготовлення коліс під час ремонту машин, проведення експертизи, пов’язаної з виясненням причин поломок і аварій, а також під час контролю розмірів у процесі виготовлення зубчастих коліс.

До основних параметрів циліндричного прямого зубчастого колеса відносять: кількість зубців z, модуль m, кут α, діаметр d ділильного кола, діаметр d_а кола вершин, діаметр d_f кола западин, діаметр d_b основного кола, крок р зубів по ділильному колу, товщина S та ширина е зуба по ділильному колу, висота h_a головки і висота h_f ніжки зуба, висота h зуба,радіусом ρ_о галтелі переходу ніжки зуба в коло западин Модуль m та кут зачеплення α є величинами стандартними.

Усі розрахункові параметри зубчатого колеса визначаються через модуль зуба такими залежностями:

крок по дузі ділильного кола

P= π∙m; (7.1)

крок по дузі основного кола

P_b= p∙cosα = π∙m∙ cosα; (7.2)

діаметр ділильного кола

d= m ∙z; (7.3)

діаметр основного кола

d_b= d∙cosα = m∙z∙cosα; (7.4)

діаметр кола вершин

d_a = m∙ (z+2); (7.5)

діаметр кола западин

d_f= m∙ (z-2,5); (7.6)

товщина зуба та ширина западини

S= e= = ; (7.7)

висота зуба

h= h_f +h_a= 2,25∙m; (7.8)

висота вершини зуба

h_a = m; (7.9)

висота ніжки зуба

h_f =1,25∙m; (7.10)

радіус галтелі

ρ_o = 0,38∙m ≈ 0,4∙m (7.11)

Стандартні колеса в техніці застосовуються рідко. Більшість передач складається із так званих коригованих, виправлених коліс. Такі колеса дозволяють одночасно зменшити габарити передачі, підвищити міцність зуба, знизити питомий тиск, покращити плавність зачеплення тощо. Часто багатоланкові зубчасті передачі взагалі не можна створити із стандартних коліс. Це стосується, передусім, співвісних передач, наприклад, коробок швидкостей, подач і т. п. У таких передачах треба для однієї або декількох пар коліс одночасно задовольнити такі дві суперечливі вимоги як забезпечення заданої міжосьової відстані і фіксованого передаточного відношення.

Усі евольвентні зубчасті колеса виготовляються ріжучим інструментом, в основу якого покладено вихідний твірний контур, форма і розміри якого стандартизовані (ГОСТ 13755-81). Вихідний твірний контур має форму зубчастої рейки (рис. 7.1) і характеризується такими стандартними параметрами, як модуль m зачеплення, кут профілю зуба α = 20˚, коефіцієнт висоти вершини зуба = 1,0 і коефіцієнт радіального затвора = 0,25.

Рис. 7.1

Лінія рейки, на якій товщина зуба дорівнює ширині западини, називається ділильною прямою.

При виготовленні стандартного колеса ділильна пряма ріжучого інструменту дотикається до початкового кола колеса і перекочується по ньому без ковзання.

Якщо ріжучий інструмент змістити відносно заготовки на деяку величину X так, щоб ділильне коло колеса не дотикалося до ділильної прямої рейки або перетинало її, то одержимо колесо, кориговане відносно стандартного. У коригованого колеса товщина зуба не дорівнює ширині западини (s e) і не дорівнює половині кроку, висота вершини зуба не дорівнює модулю ( ), а в інших і кут зачеплення не дорівнює куту профілю рейки. Тобто, форма зуба у коригованого колеса змінюється порівняно із зубом стандартного колеса.

Абсолютне зміщення X, як і інші параметри зачеплення, виражається через модуль m

X = x∙m, (7.12)

де x – коефіцієнт зміщення.

Прийнято вважати зміщення від’ємним, якщо інструмент зміщується до центра заготовки, і навпаки.

При проектуванні зубчастої передачі модуль зачеплення m визначається розрахунками зуба на міцність.

Д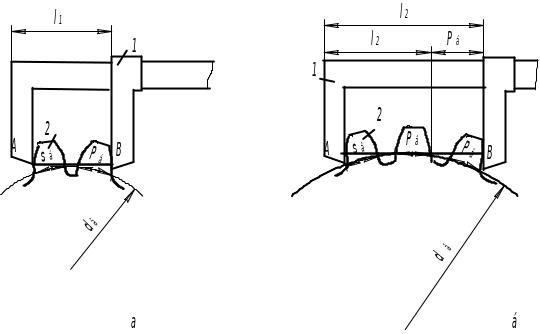 ля існуючого евольвентного зубчастого колеса модуль можна розраховувати шляхом вимірювань, скориставшись основною властивістю евольвенти: «нормаль, проведена у будь-якій точці дотику евольвентних профілів, є дотичною до основного кола».

Рис. 7.2

Штангенциркулем 1, охопивши n зубів 2, необхідно виміряти спочатку розмір l₁ (рис. 1.2, а), потім, охопивши n + 2 зубів, виміряти розмір l₂ (рис. 4.2, б). В обох випадках пряма АВ, що з’єднує точки А і В дотику губок штангенциркуля і боковими поверхнями зубів, є спільною нормаллю двох евольвент і дотичною в точці К до основного кола. Щоб губки штангенциркуля торкалися саме евольвентних ділянок профілів зубів, треба число n обирати згідно з рекомендаціями таблиці 7.1.

Таблиця 7.1

z	12-18	19-27	28-36	37-45	46-54	55-63	34-72
n	2	3	4	5	6	7	8

Різниця l₂-l₁ буде відповідати відстані між однойменними профілями сусідніх зуб’їв по нормалі. Цей відрізок нормалі являє собою розгортку дуги основного кола, що дорівнює основному кроку зачеплення

l₂-l₁= _b= π∙m∙cosα. (7.13)

Звідки

m = , (7.14)

де cosα = 20˚ = 0,9397; π = 3,14.

Одержане значення модуля в міліметрах треба округлити до найближчого стандартного значення СТ СЭВ 310-76 та ГОСТ 2.403-75 (табл. 7.2). Відхилення від стандартних величин модуля можуть бути результатом неточності вимірювань.

Таблиця 7.2

1-й ряд	0,8	1,0	1,25	1,5	2	2,5	3	4	5	6	8	10
2-й ряд	0,9	1,125	1,375	1,75	2,25	2,75	3,5	4,5	5,5	7	9	11

Модуль m можна визначити також, скориставшись формулами

m = ; (7.15)

m = , (7.16)

де d_a, d_f – діаметри кіл вершин та западин.

При парному числі z ці діаметри вимірюють штангенциркулем безпосередньо (рис. 7.3, а). Якщо число z непарне, то спочатку треба виміряти діаметр отвору d_отв та розміри l₃ i l₄ (рис. 7.3, б), а потім обчислити діаметри кіл вершин та западин за формулами:

d_a= d_отв+2∙l₃; d_f = d_отв+2∙l₄. (7.17)

Рис. 7.3

Інші геометричні параметри колеса обчислюють за формулами.

Визначена за формулою товщина зуба S повинна мати досить близьке значення до розрахункової товщини зуба по хорді ділильного кола:

S_x = d ∙sinφ, (7.18)

де = – половина кутової товщини зуба.

Цю ж товщину зуба S_x можна виміряти безпосередньо штангензубоміром (рис. 7.4), який має дві шкали з ноніусами. Шкала 1 призначена для вимірювання товщини зуба, а шкала 2 – радіальної відстані Н від кола вершин до хорди ділильного кола.

Рис. 1.4

Спочатку обчислюють величину Н за формулою

H = (7.19)

Потім на цій відстані фіксують установчу пластинку 3. Штангензубомір розміщують на зубі так, щоб пластина 3 обперлася на вершину зуба. Зсувають губки інструменту до дотику з боковими поверхнями зуба і за школою 1 визначають його товщину S_x. Розрахункова та виміряна товщини зуба S_x можуть не співпасти, що пояснюється похибкою вимірювання.