
- •Розділ і. Теоретичні основи методики навчання диференціальних рівнянь в педагогічних університетах
- •Диференціальні рівняння як складова вивчення математики в педагогічних вищих навчальних закладах
- •Психолого-педагогічні основи навчання вивчення диференціальних рівнянь
- •Теоретичні основи вивчення диференціальних рівнянь Навчальна програма вивчення курсу «Диференціальні рівняння» для студентів фізико-математичного факультету вищих навчальних педагогічних закладів
- •I. Загальні відомості
- •II. Перелік дисциплін, знання яких необхідне для вивчення курсу
- •III. Цілі і завдання дисципліни
- •IV. Методи навчання та інформаційно-методичне забезпечення
- •V. Форми оцінювання
- •VII. Література до курсу:
- •Дидактичні і методичні вимоги до академічної лекції
- •Основні вимоги до практичних та семінарських занять
- •Основні вимоги до контролю та корекції
- •Тестові завдання закритої форми
- •Тестові запитання відкритого типу
- •Розділ іі. Методика навчання диференціальних рівнянь в педагогічних університетах
- •2.1. Розробка лекцій, практичних робіт, опорних конспектів
- •Методичні особливості вивчення змістовного модуля I «Основні поняття теорії диференціальних рівнянь. Рівняння з відокремлюючими змінними»
- •Теми лекцій, практичних занять та завдання для самостійної роботи для змістовного модуля I
- •Логічна структура вивчення змістовного модуля I
- •Розв’язані відносно похідної (з відокремлюючими змінними)
- •Короткий довідник з теми «Диференціальні рівняння I порядку»
- •Розробка лекцій до змістовного модуля і Лекція 1
- •План лекції
- •Список літератури
- •Текст лекції
- •Лекція 2
- •План лекції
- •Список літератури
- •Текст лекції
- •Лекція 3
- •План лекції
- •Список літератури
- •Текст лекції
- •Лекція 4
- •План лекції
- •Список літератури
- •Текст лекції
- •2. Рівняння Бернуллі
- •Лекція 5
- •План лекції
- •Список літератури
- •Текст лекції
- •Р озробка практичних занять для змістовного модуля і Практичне заняття 1
- •План заняття
- •Список літератури
- •Хід заняття
- •Практичне заняття 2
- •План заняття
- •Список літератури
- •Хід заняття
- •Практичне заняття 3
- •План заняття
- •Список літератури
- •Хід заняття
- •Практичне заняття 4
- •План заняття
- •Список літератури
- •Хід заняття
- •Семантичний конспект до змістовного модуля I
- •2.2. Контроль та корекція
- •Індивідуальні творчі завдання до змістовного модуля I
- •Модульна контрольна робота змістовного модуля I
- •Висновки
- •Використана література
Логічна структура вивчення змістовного модуля I

Звичайне диференціальне рівняння
n-ого порядку
РОЗВ’ЯЗАТИ
диференціальне рівняння – це означає
знайти ВСІ
функції y,
які задовольняють це рівняння в області
визначення всіх незалежних змінних.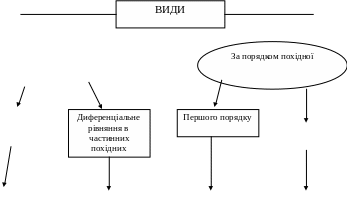






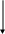


Не розв’язані
відносно похідної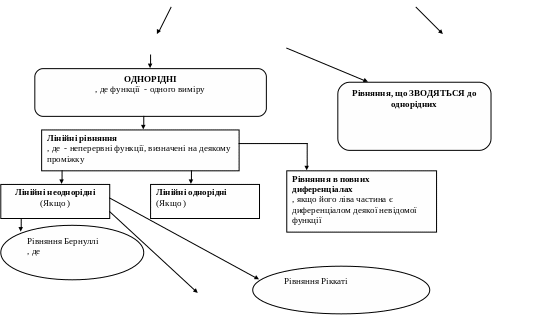

Розв’язані відносно похідної (з відокремлюючими змінними)

Короткий довідник з теми «Диференціальні рівняння I порядку»
Тип рівняння |
Стандартна форма запису |
Особливості |
Метод розв’язування |
З відокремлюючими змінними |
|
При диференціалах – похідна функції, яка залежить одна від x, інша – від y |
|
|
Права частина – добуток функцій, які залежать одна від x, інша – від y |
|
|
Однорідне |
|
Права частина – однорідна функція нульового порядку |
|
|
|
|
|
В повних диференціалах |
|
|
|
Лінійне |
|
Першої
степіні відносно
|
|
|
Першої
степіні відносно
|
|
|
Бернуллі |
|
Відрізняється від лінійного правою частиною |
Аналогічно лінійним |
Розробка лекцій до змістовного модуля і Лекція 1
Тема: «Диференціальні рівняння, основні визначення»
Мета:
вивчення основних положень та визначень з теми «Диференціальні рівняння»;
ознайомлення із виникненням та застосуванням диференціальних рівнянь;
поглиблення, розширення знань, отриманих раніше при вивченні розділів диференціального і інтегрального числення з курсу математичного аналізу, алгебри та геометрії.
розвиток наукового мислення та пам’яті;
виховання культури математичного запису і мовлення.
При вивченні теми студенти повинні:
знати: означення диференціального рівняння та основні поняття, які його стосуються (види, порядок, степінь, розв'язок);
уміти: визначати диференціальне рівняння з переліку рівнянь, складати рівняння за умовою задачі, що приводить до диференціального рівняння;
здатні: знаходити невизначений інтеграл (з курсу математичного аналізу).
Основні поняття: диференціальне рівняння (ДР), звичайне ДР, ДР у частинних похідних, порядок ДР, степінь, розв'язок.
Обладнання: підручники, дидактичний матеріал (таблиці), креслярські матеріали, мультимедійний проектор, комп’ютер.
Час: 2 год.
План лекції
Поняття диференціального рівняння і його розв'язку.
Приклади задач, які приводять до диференціального рівняння.
Список літератури
Еругин Р.П. и др. Курс обыкновенных дифференциальных уравнений.
Пономарев К.К. Составление дифференциальных уравнений.
Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.
Давидов М.О. Курс математичного аналізу: Підручник: У 3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. – 2-ге вид., перероб. і допов. – К.: Вища школа, 1991 – 336 с.
