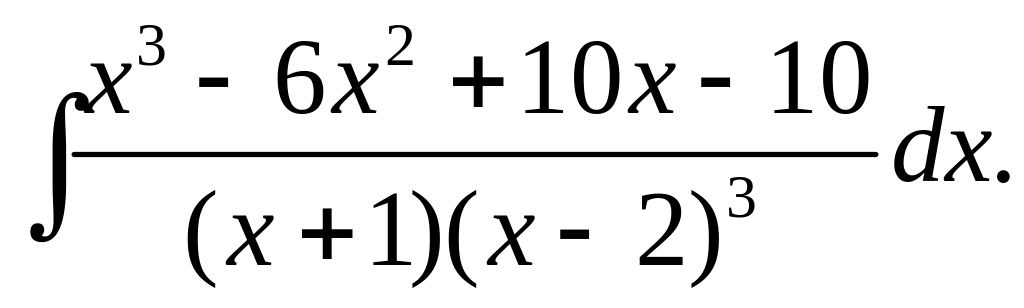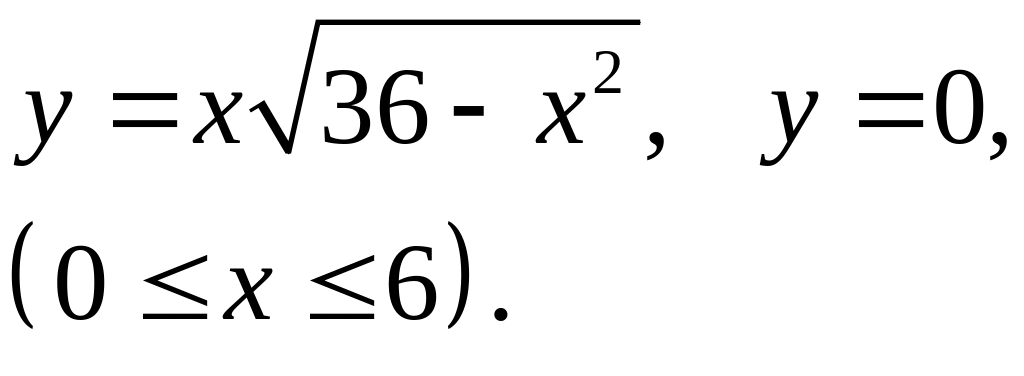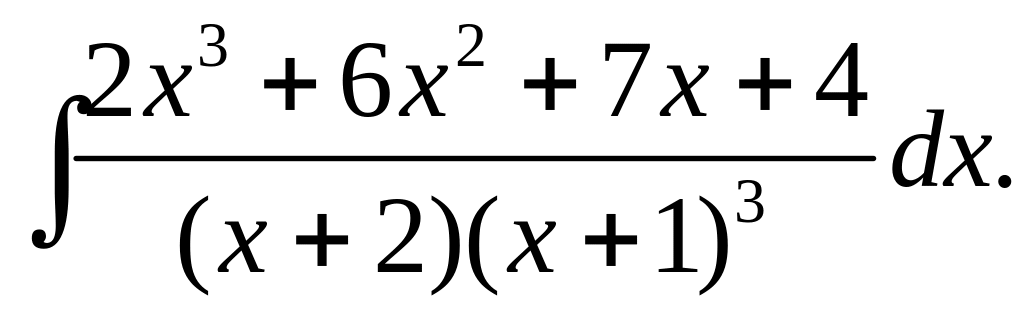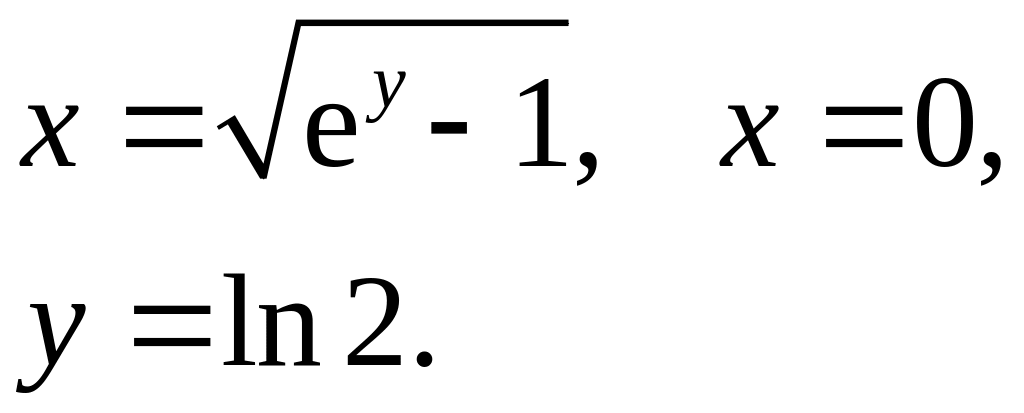Р озробка практичних занять для змістовного модуля і Практичне заняття 1

Тема: «Диференціальні рівняння з відокремлюючими змінними»

Мета:

• вироблення вмінь та удосконалення навичок розв’язувати загальні диференціальні рівняння з відокремлюючими змінними;

• вироблення вмінь зводити диференціальне рівняння до рівняння з відокремлюючими змінними;

• розвиток продуктивного мислення;

• виховання математичної культури.

При вивченні теми студенти повинні:

знати: означення диференціального рівняння з відокремлюючими змінними, методи їх розв'язування;

уміти: застосовувати знання для розв'язування рівняння з відокремлюючими змінними, зводити рівняння до рівняння з відокремлюючими змінними;

здатні: розв'язувати загальні рівняння з відокремлюючими змінними.

Обладнання: підручники, дидактичний матеріал (таблиці), картки із самостійною роботою, мультимедійний проектор, комп’ютер.

Час: 2 год.

План заняття

I. Організаційний момент.

II. Актуалізація опорних знань (термінологічний диктант).

III. Вироблення вмінь та навичок.

IV. Контроль.

Список літератури

1. Pudy A.E., Rakov S.A. Mathematical Analysis. Differential Equations.

2. Давидов М.О. Курс математичного аналізу: Підручник: У 3 ч. Ч. 2. Функції багатьох змінних і диференціальні рівняння. – 2-ге вид., перероб. і допов. – К.: Вища школа, 1991 – 336 с.

3. Матвеев Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям.

4. Самойленко Ф.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения, примеры и задачи.

5. Филиппов А.Ф. Сборник задач по обыкновенным дифференциальным уравнениям.

Хід заняття

I. Привітання із студентами, повідомлення мети й завдань заняття, перевірка присутніх.

II. Мета етапу: визначення рівня засвоєння теоретичного матеріалу студентами та рівня підготовки до практичного заняття.

Термінологічний диктант. Викладач називає терміни, які студенти вивчали на першій та другій лекції, вони записують відповіді. Після закінчення – взаємоперевірка (сусід перевіряє у сусіда), правильні відповіді на проекторі.

Перший варіант Яке рівняння називається диференціальним? Записати загальний вид диференціального рівняння першого порядку. Що називається інтегральною кривою диференціальне рівняння у' =F (х; у)? Що називається загальним розв'язком диференціального рівняння у' =F (х; у)?	Другий варіант Яке диференціальне рівняння називається рівнянням першого порядку? Записати загальний вид диференціального рівняння. Що називається розв'язком диференціального рівняння у' =F (х; у)? Як із загального розв'язку одержати частинний розв'язок?
5. Яке диференціальне рівняння називається рівнянням з відокремлюючими змінними?

III. Мета етапу: вироблення вмінь та удосконалення навичок розв’язувати загальні диференціальні рівняння з відокремлюючими змінними.

Розв'язування задач та вправ.

1. Знайти загальний розв'язок рівняння:

Розв'язування.

- загальний розв'язок рівняння.

2. Знайти сім’ю розв’язків рівняння .

Розв'язування. Розглянемо рівняння

(1)

Його права частина f (х₀; у₀) неперервна при у 0, тобто у верхній півплощині, включаючи вісь, О_х (область D'₁). Функція неперервна при у>0, тобто у верхній півплощині, виключаючи вісь О_х (область D₁). Рівняння (1) має сім'ю розв'язків:

, , , (2)

де С – довільна стала. Формула (2) називається загальним розв'язком рівняння (1). Тоді у = (х+с)², при чому х+с>Q. В півплощині у>0 функція у = (х+с)² є розв'язком початкового рівняння.

3. Знайти загальний інтеграл диференціального рівняння (відповідь представити у вигляді )

Розв'язування.

5. Знайти загальний інтеграл диференціального рівняння.

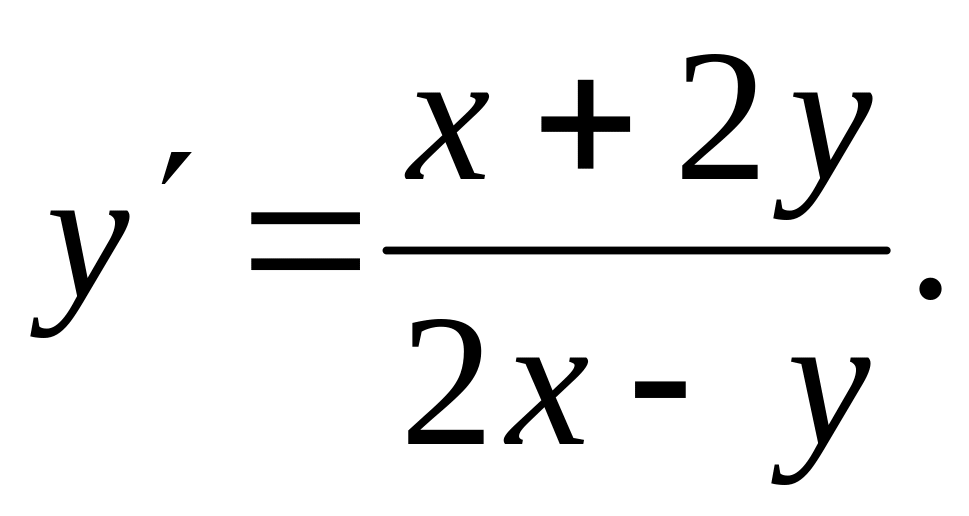
Розв'язування.

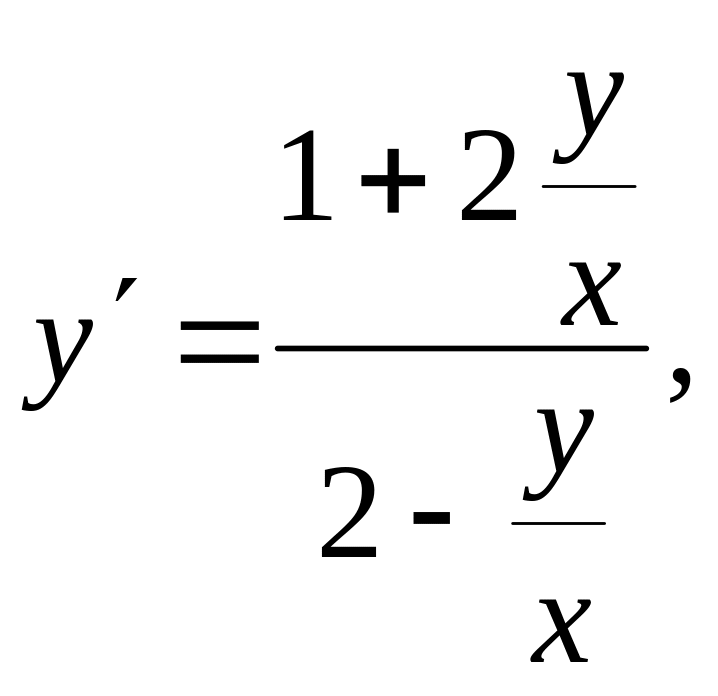
Вводимо заміну

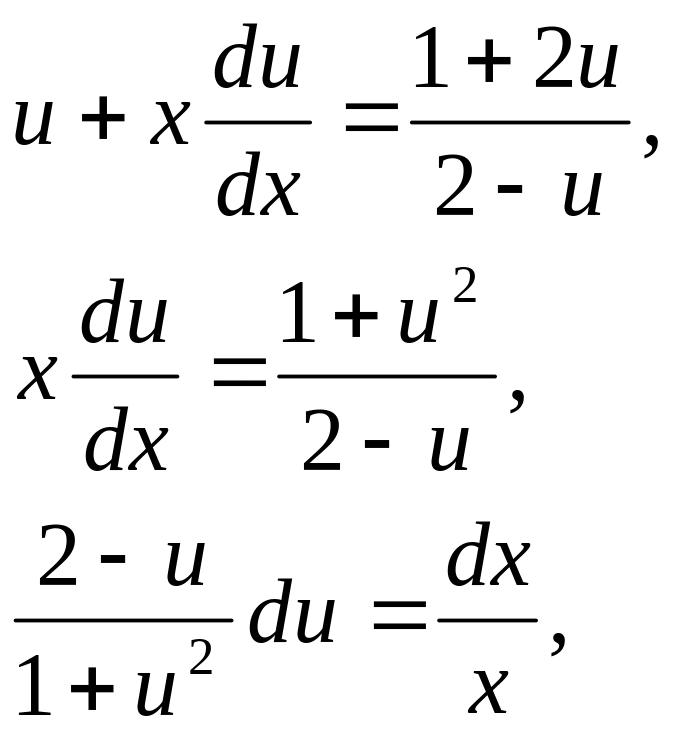
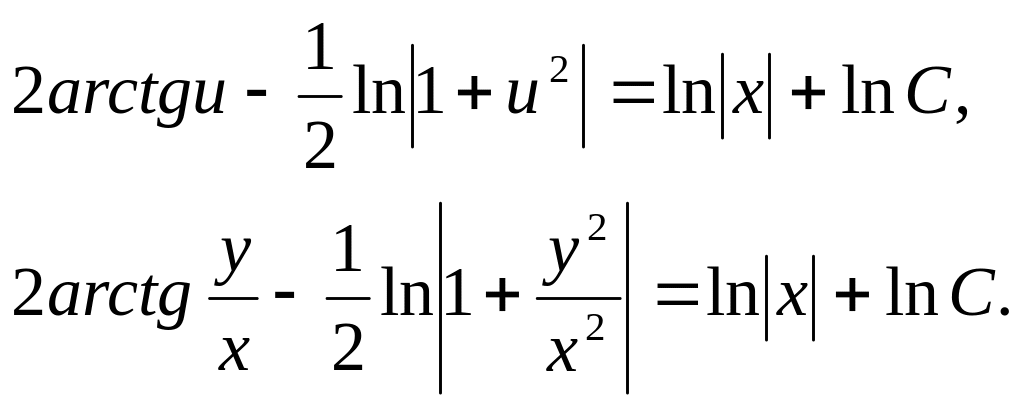
6. Знайти загальний інтеграл диференціального рівняння

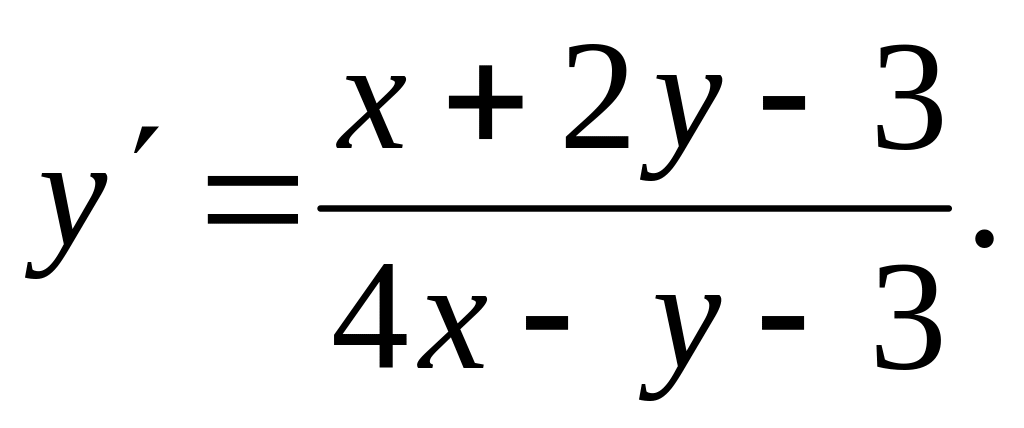
Розв'язування.

Нехай

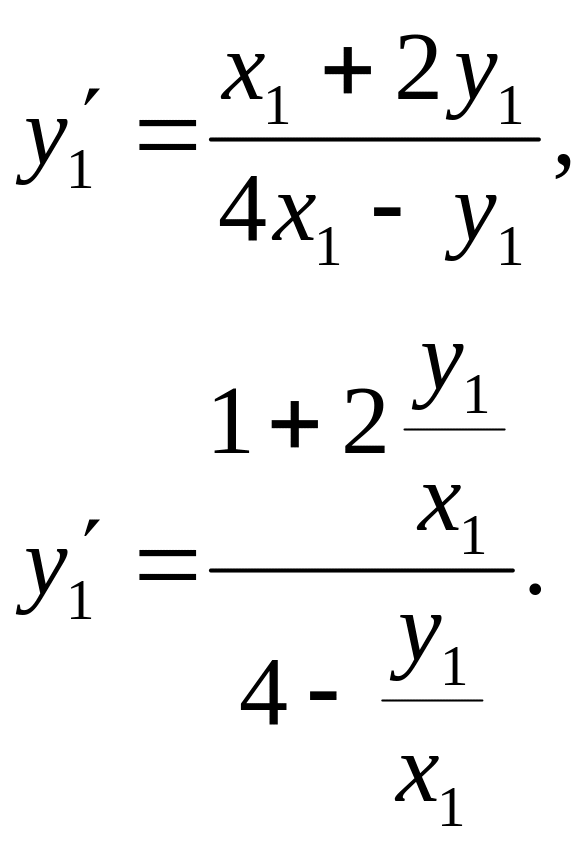
Вводимо заміну

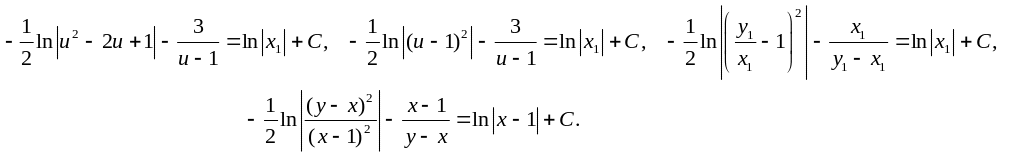
IV. Мета етапу: перевірка базових вмінь та навичок студентів знаходити загальний інтеграл функції (з курсу математичного аналізу).

Самостійна робота (за варіантами). Перевіряється викладачем, результати оголошуються на наступному занятті.

1. Обчислити невизначені інтеграли: А) Б) 2. Знайти площу фігури, яка обмежена графіками функцій.

1. Обчислити невизначені інтеграли: А) Б) 2. Знайти площу фігури, яка обмежена графіками функцій.

Домашнє завдання: за підручником [1] розв’язати на ст. 11 (P.L. 1.1.) № 1 (10-15), № 2 (9-12).