5.3. Деление твердых тел на металлы, диэлектрики и полупроводники

Зонная теория твердого тела позволяет с единых позиций объяснить существование металлов, полупроводников и диэлектриков. В зависимости от степени заполнения валентной зоны электронами и ширины запрещенной зоны. Возможны три случая, представленные на рис. 5.8, а,б,в.

В случае, изображенном на рис. 5.8, а, электроны заполняют валентную зону не полностью. Если в кристалле создано слабое электрическое поле, то за счет имеющихся свободных уровней электроны смогут участвовать в создании тока, и изменять свою энергию переходя на более высокие уровни. Кристалл с подобным заполнением валентной зоны является металлом. К металлам (проводникам) относятся так же вещества, у которых валентная зона перекрывается с зоной проводимости (рис. 5.3 и 5.8, б).

На рис. 5.8, в представленная зонная диаграмма на которой все уровни валентной зоны при абсолютном нуле температуры заняты электронами. Для увеличения энергии электрона, ему необходимо сообщить энергию не меньше чем ширина запрещенной зоны , которая составляет единицы ЭВ. Электрическое поле не очень большой напряженности на расстоянии порядка межатомного, такую энергию сообщить не в состоянии. В таком случае при Т= ОК кристалл не проводит электрический ток и, следовательно, является диэлектриком или полупроводником.

Условно считают, что если эВ, то кристалл является полупроводником. Для диэлектриков эВ. При комнатных температурах средняя энергия теплового движения электрона имеет порядок КТ и значительно меньше, чем ∆Е₃ в беспримесных (собственных) полупроводниках. Однако, у части электронов энергия может быть больше ∆Е₃ и они способны ”перейти” из валентной зоны в зону проводимости. Такой процесс называется тепловой генерацией (рис. 5.8, в). В зоне проводимости электроны способны участвовать в создании тока.

В каждом акте тепловой генерации возникает свободный электрон в зоне проводимости и свободное место (“дырка”) в валентной зоне. Наряду с процессом тепловой генерации существует и обратный процесс – рекомбинация (рис. 5.8, в), при котором электрон из зоны проводимости переходит в валентную зону. В условиях постоянства температуры за счет динамического равновесия между процессами генерации и рекомбинации устанавливаются равновесные концентрации электронов и дырок.

В диэлектриках из-за больших значений ∆Е₃ концентрация электронов в зоне проводимости пренебрежимо мала, поэтому диэлектрики являются изоляторами.

5.4 Движение электрона в кристалле под действием электрического поля. Эффективная масса.

Движение электрона в периодическом потенциальном поле кристалла описывается волновым пакетом составленным из плоских волн с близкими значениями волнового числа k. Групповая скорость волнового пакета отождествляется со скоростью движения электрона.

Из определения групповой скорости

, (5.14)

где – частота волны как функция к, и соотношения , находим

. (5.15)

Ускорение электрона в кристалле найдем продифференцировав выражение (5.15) по t:

. (5.16)

Учитывая корпускулярно-волновое соотношение и дифференцируя его по t получим:

. (5.17)

Если кристалл помещен в электрическое поле, то изменение импульса электрона равно действующей на него силе

. (5.18)

Подставив (5.17) и (5.18) в (5.16), получим

. (5.19)

Из сравнения выражения (5.19) с уравнением второго закона Ньютона следует, что роль массы по отношению к внешней силе играет величина

. (5.20)

Величина m* - получила название эффективной массы. Из-за взаимодействия электрона с кристаллической решеткой эффективная масса может существенно отличаться от массы свободного электрона.

С учетом внешней силы и силы действующей на электрон в кристалле уравнение второго закона Ньютона можно записать в виде:

. (5.21)

Если выражение (5.20) подставить в формулу (5.19), то получим

. (5.22)

Сравнивая уравнения (5.21) и (5.22) приходим к заключению, что действие силы учитывается эквивалентным образом за счет введения вместо массы свободного электрона эффективной массы.

В соответствии с формулой (5.20) изменения эффективной массы определяется изменением . График функции E(k) для первой зоны Бриллюэна представлен на рис. 5.9.

У электрона, находящегося в нижней части зоны (точка А на рис. 5.9, а) эффективная масса , так как . Зависимость E(k) на участке ОА не отличается от параболы, поэтому скорость электрона под действием внешней силы растет, а эффективная масса приблизительно равна массе свободного электрона (рис. 5.9 б).

В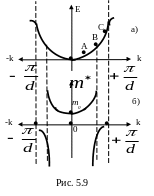 точке перегиба (точка В на рис. 5.9, а) и, следовательно, в соответствии с формулой (5.20) . Это означает, что в точке В действие силы компенсируется силой . При дальнейшем увеличении волнового вектора (точка С на рис. 5.9 а) электрона под действием внешнего электрического поля того же направления скорость электрона уменьшается, так как он получает отрицательное ускорение ; направленное противоположно силе .

Покажем, что поведение электронов в верхней части зоны где их эффективная масса , можно описать с помощью частиц с положительным зарядом +е, положительной эффективной массой .

Уравнение движение электрона во внешнем электрическом поле с напряженностью имеет вид:

. (5.23)

Перенесем знак минус из первой части уравнения в левую, тогда получим эквивалентное уравнение

. (5.24)

Учитывая, что -m^*>0 действительно убеждаемся в возможности замены при описании поведения электрона в верхней части зоны частицей с положительной массой и положительным зарядом. Такую частицу принято называть дыркой.

Если в верхней части зоны имеются вакантные состояния их отождествляют с дырками, так как отсутствие электрона на вакантном уровне, эквивалентно наличию на нем положительно заряженной частицы (+e) с положительной эффективной массой -m^*>0.

Движение дырки не связано с движением реальной положительно заряженной частицы. По кристаллу движется электрон, переходя от одного атома к другому на «свободное» место.

Само свободное место (дырка), очевидно перемещается в противоположном направлении. Перенос заряда, связанный с перемещением дырок под действием электрического поля лежит в основе так называемой дырочной проводимости.

В заключение отметим, что эффективная масса электрона в кристалле не определяет его инерционные и гравитационные свойства. Введение этой величины дает возможность, учитывая сложный характер взаимодействия электрона с решеткой при его движении под действием внешнего электрического поля, пользоваться простыми формулами движение электрона в нижней части энергетической зоны:

(5.25)