- •Элементы математической логики
- •, Если ;
- •, Если , , ;
- •, Если , .
- •Теория множеств
- •26. Решите задачу:
- •27. Решите задачу:
- •28. Решите задачу:
- •Бинарные отношения
- •Метод математической индукции
- •Комбинаторика
- •Типовые контрольные работы
- •Вариант 1
- •Вариант 2
- •Вариант 1
- •Вариант 2
- •Вариант 1
- •Вариант 2
- •Используемая литература
26. Решите задачу:
В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык: 6 человек – английский язык, 7 человек – немецкий язык, 4 человека – оба языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Только немецкий? Сколько человек знает только один язык?
27. Решите задачу:
В классе 30 учеников. Каждый из них занимается либо футболом, либо хоккеем, а 5 учеников – и хоккеем, и футболом. Сколько учеников занимается футболом, если хоккеем занимается половина учеников класса?
28. Решите задачу:
Сколько чисел содержится в множестве P, если известно, что среди них 100 чисел кратно двум, 115 – трем, 120 – пяти, 45 –шести, 38 – десяти, 50 – пятнадцати, 20 чисел – тридцати?
29. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
-
Запрос
Найдено страниц
(в тысячах)
Крейсер & Линкор
900
Крейсер
2900
Линкор
2100
Какое количество страниц (в тысячах) будет найдено по запросу «Крейсер | Линкор» ?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
30. Пусть множество А состоит из n элементов, множество B состоит из p элементов, причем p>n. Какое наибольшее и наименьшее число элементов могут содержать множества , , , ? Постройте таблицу:
|
|
|
|
|
Наибольшее число элементов |
|
|
|
|
Наименьшее число элементов |
|
|
|
|
31. Задать
множество перечислением их элементов
и найти
![]() ,
,
,
,
![]() ,
,
![]() :
:
А – множество делителей числа 12,
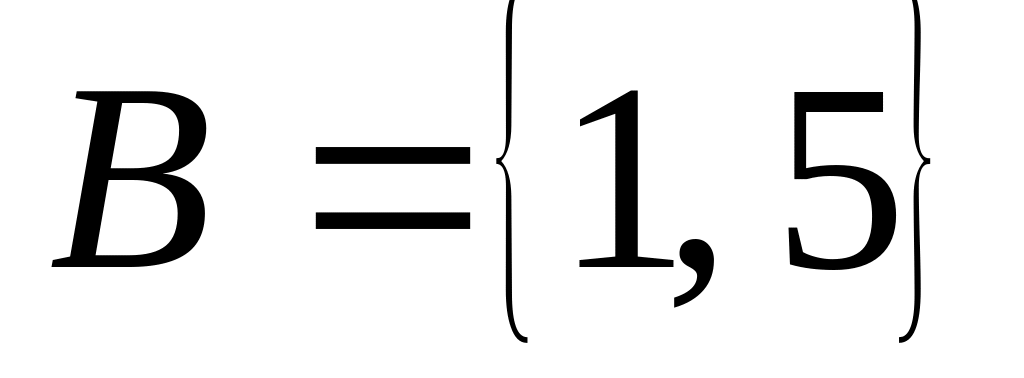 ,
С – множество нечетных чисел x
таких, что 2<x<13;
,
С – множество нечетных чисел x
таких, что 2<x<13;А – множество четных чисел x таких, что 3<x<10, B – множество делителей числа 21, С – множество простых чисел, меньших 12.
32.
Определить какой знак из множества
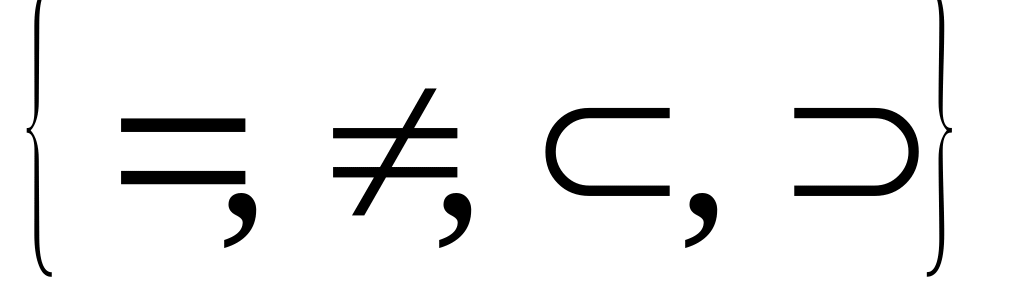 можно
поставить вместо символа «?», чтобы
полученное утверждение было верным.
можно
поставить вместо символа «?», чтобы
полученное утверждение было верным.
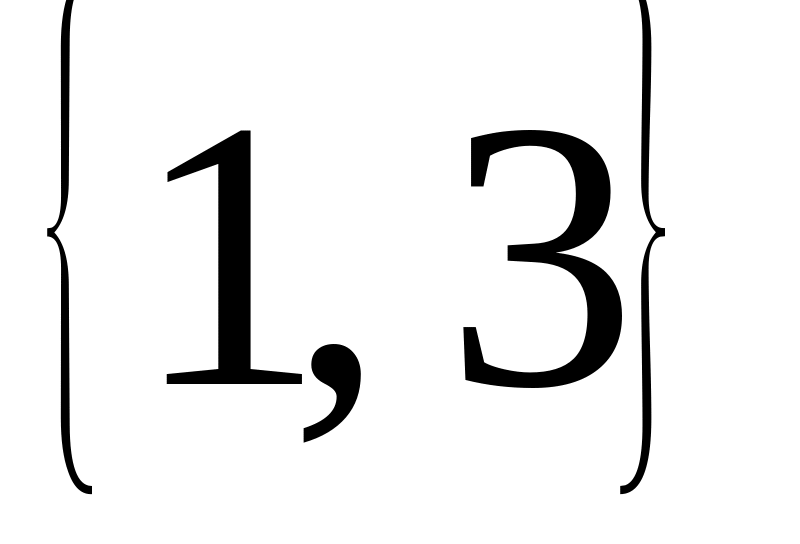 ?
?
 ;
;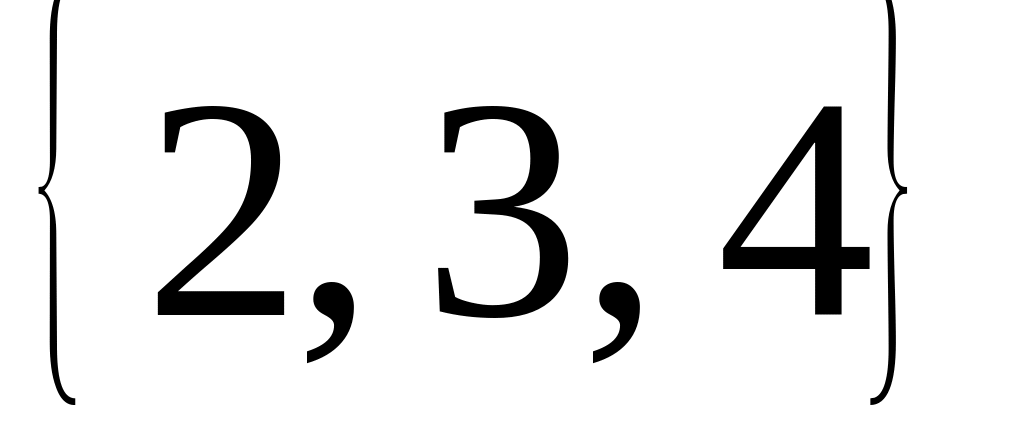 ?
;
?
;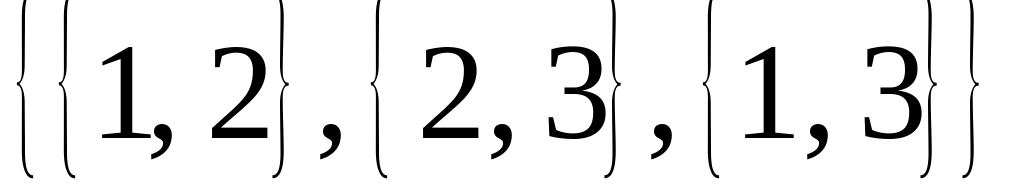 ?
;
?
; ?
;
?
;?
 ;
; ?
?
 ;
;?
 ;
;?

 ;
;
33. Верно ли, что:
Бинарные отношения
Основные понятия: Прямое произведение множеств и его свойства, бинарные отношения и их свойства, граф и график бинарного отношения, композиция бинарных отношений, инверсия, отношение эквивалентности и порядка, разбиение множества на классы, отношение сравнения по модулю. Функциональные отношения, их свойства: инъекция, сюръекция, биекция; способы задания функций, взаимно-однозначные отображения, обратная функция, условие существования обратной функции.
1.
Перечислите элементы множеств
![]() ,
,
![]() :
:
 ,
,
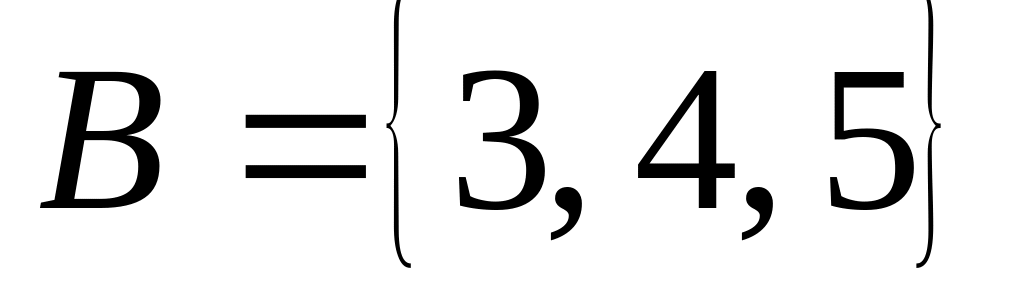 ;
;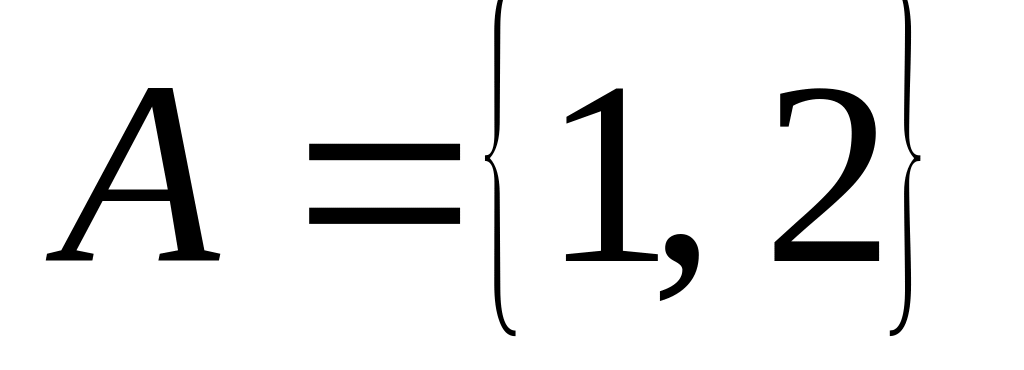 ,
,
 ;
;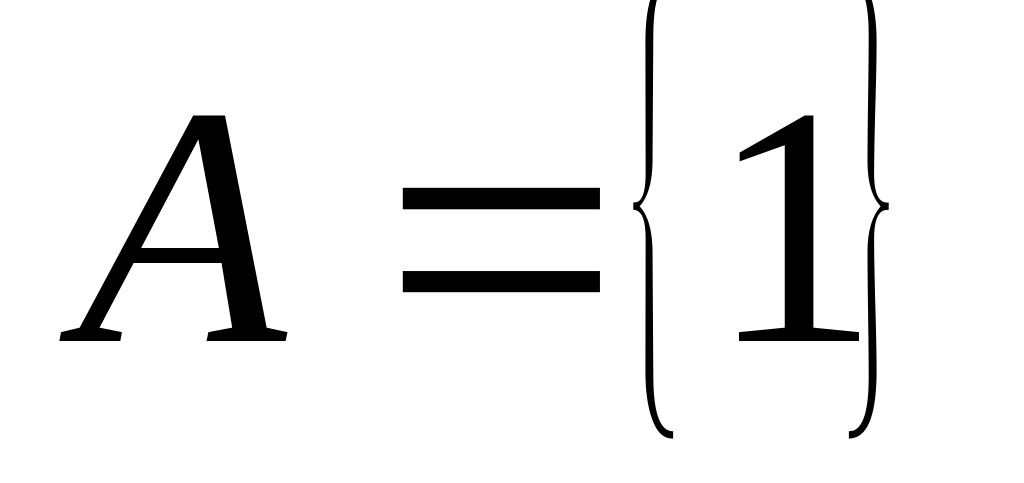 ,
;
,
;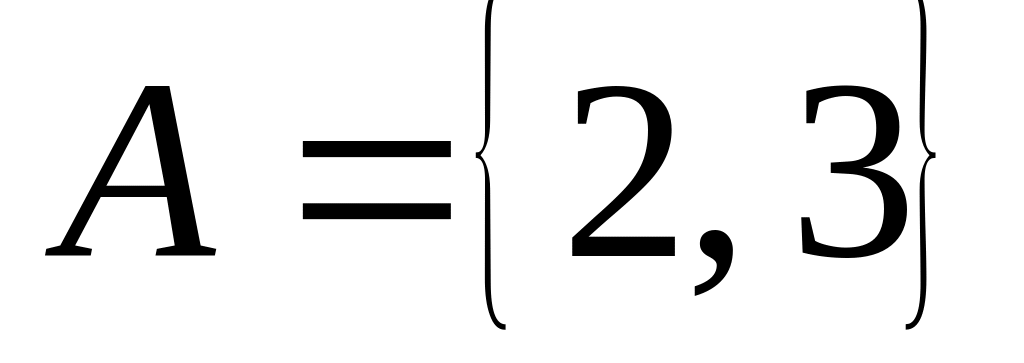 ,
,
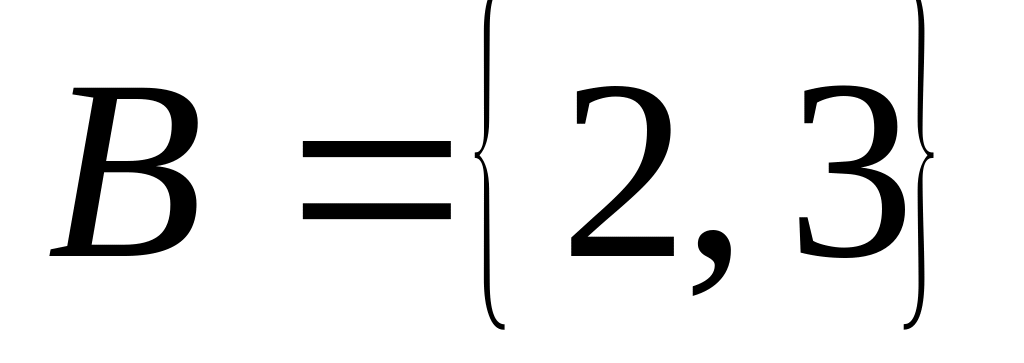 ;
;,
 ;
;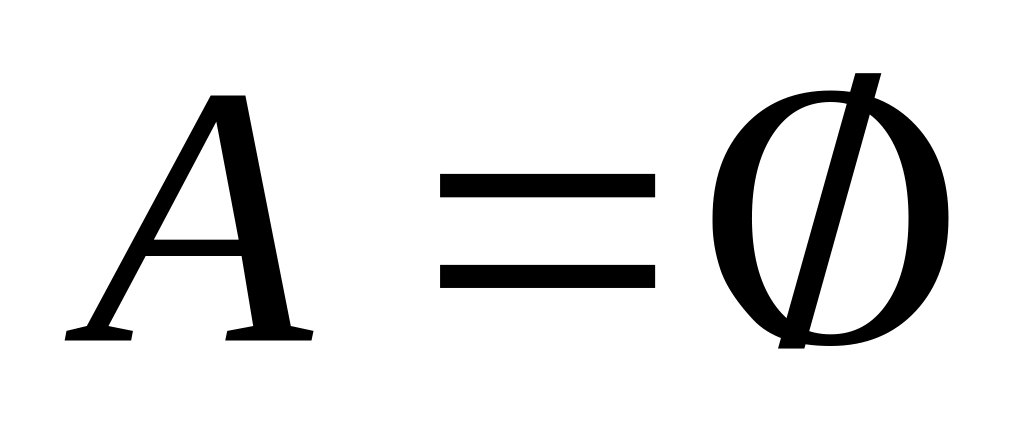 ,
,
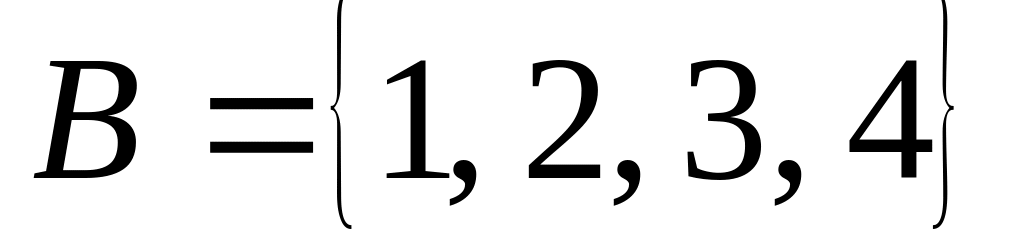 .
.
2. Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Перечислите элементы следующих множеств:
.
Перечислите элементы следующих множеств:
;
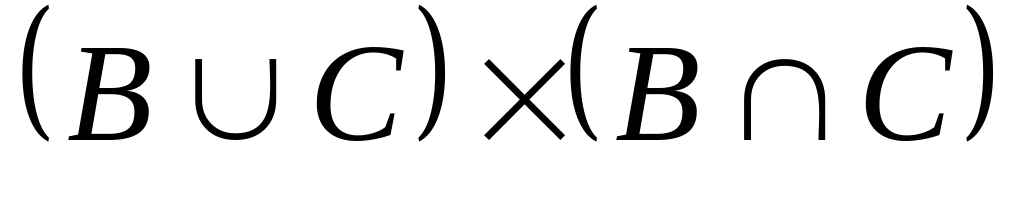 ;
;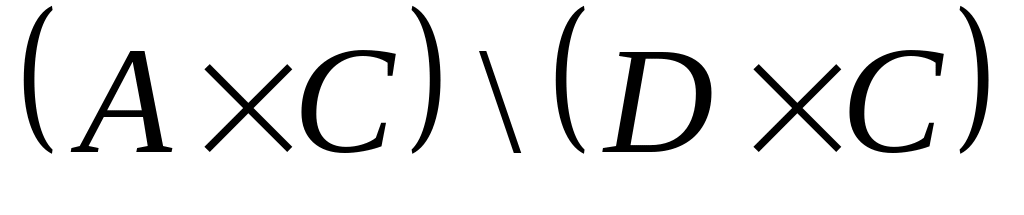 ;
; .
.
3. Пусть
![]() ,
,
,
,
![]() .
Перечислите элементы следующих множеств:
.
Перечислите элементы следующих множеств:

;
 ;
;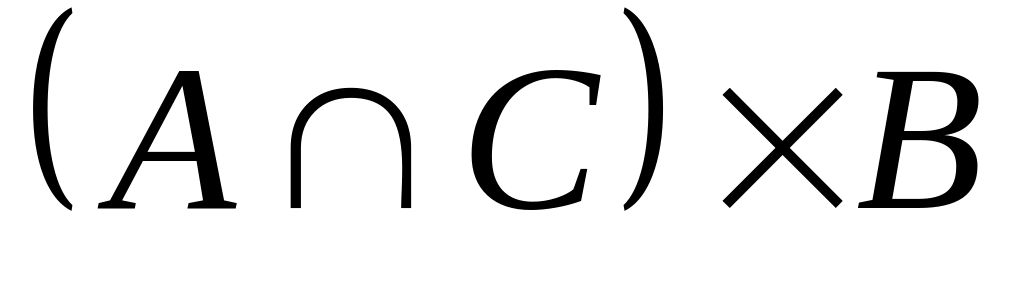 ;
;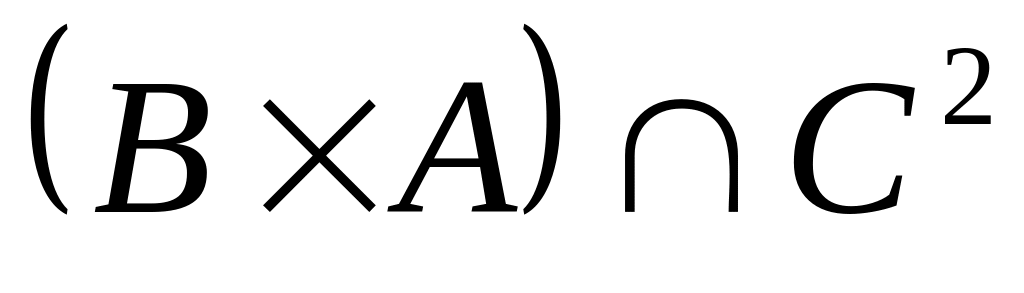 ;
;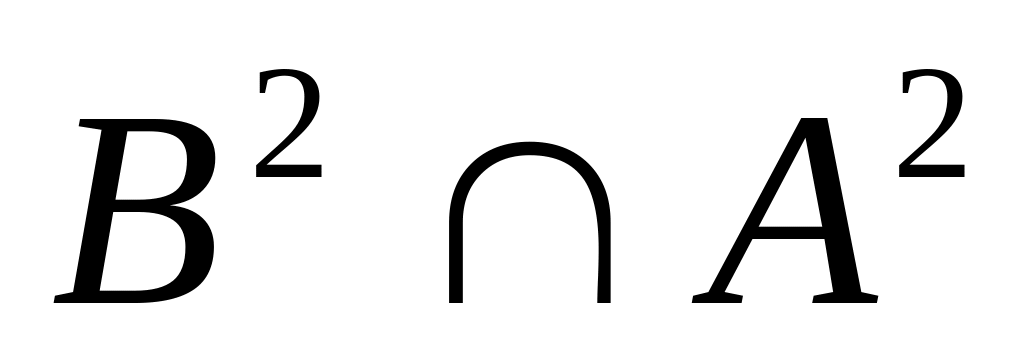 .
.
4.
Известно, что
![]() .
Установите, из каких элементов состоят
множество А и множество В.
.
Установите, из каких элементов состоят
множество А и множество В.
5. Изобразите на координатной плоскости множество:
, ;
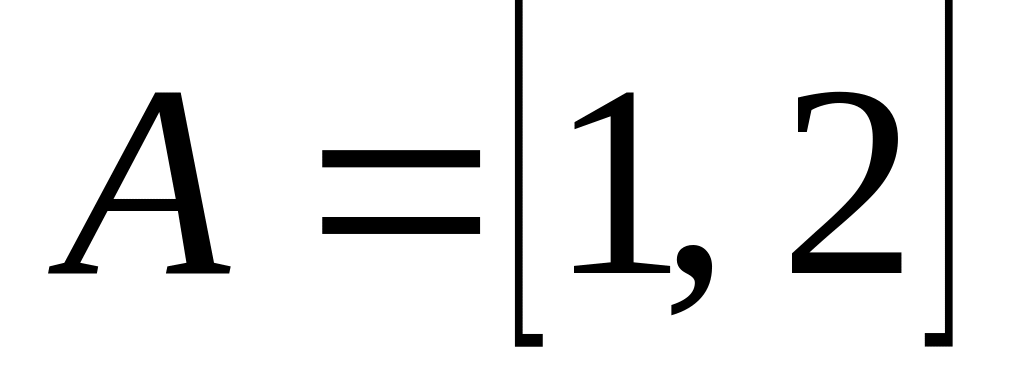 ,
;
,
; ;
; ;
; ;
;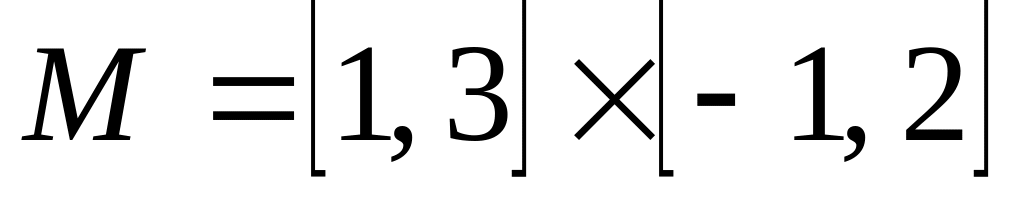 ;
; ;
; ,
где
;
,
где
;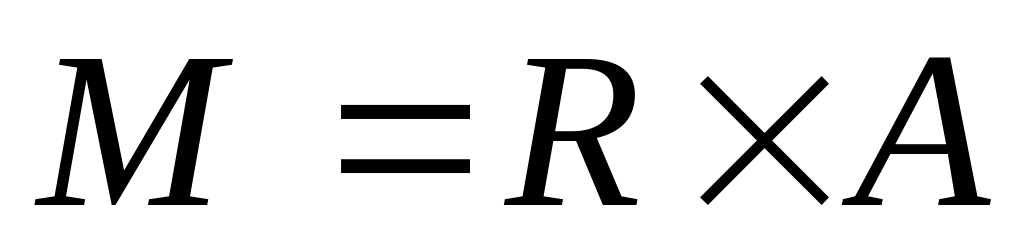 ,
где
,
где
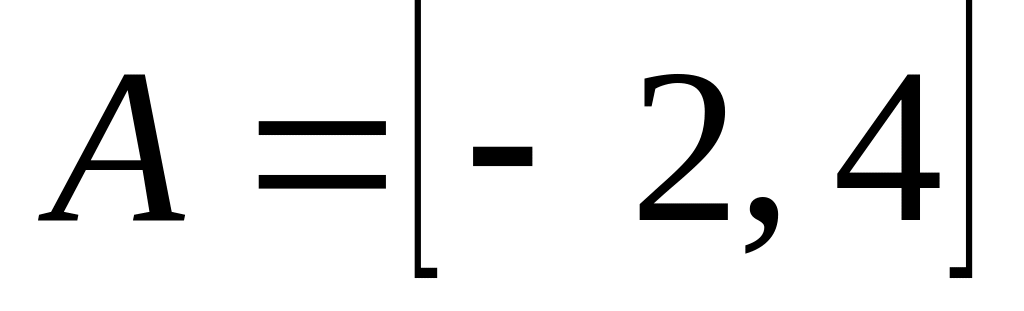 ;
; ,
где
,
где
 ,
,
 ;
; ,
где
,
где
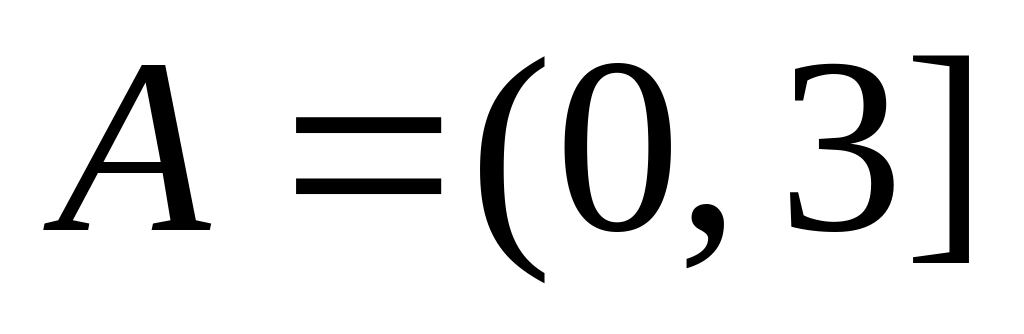 ,
,
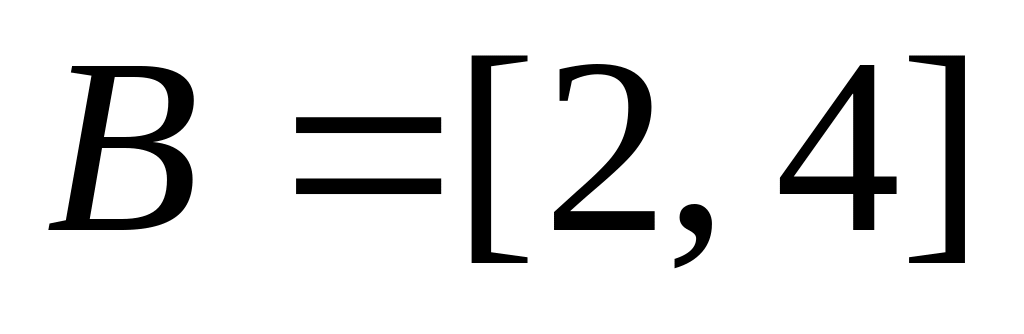 ;
;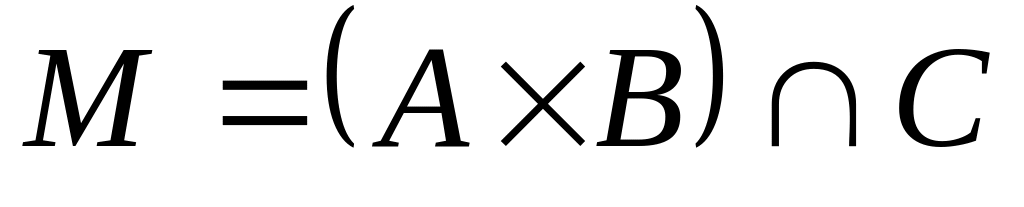 ,
где
,
где
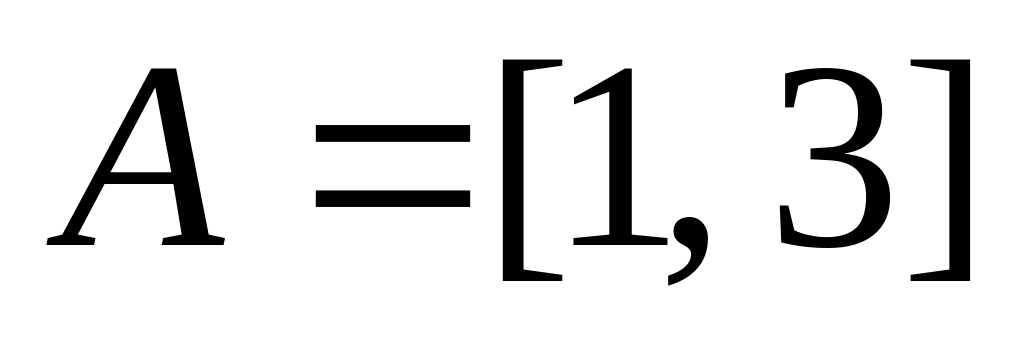 ,
,
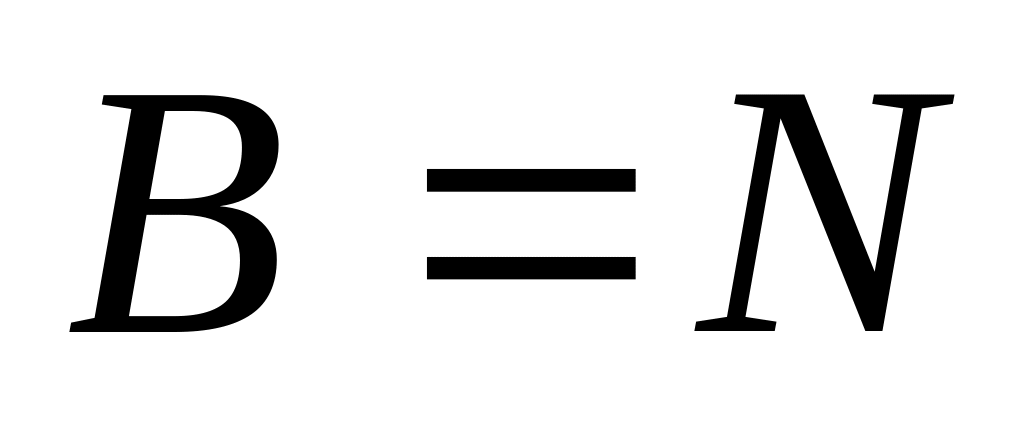 ,
,
 ;
; ,
где
,
где
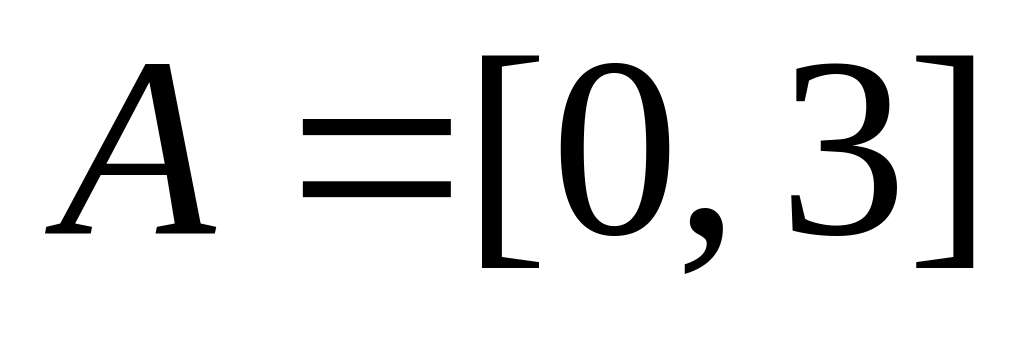 ,
,
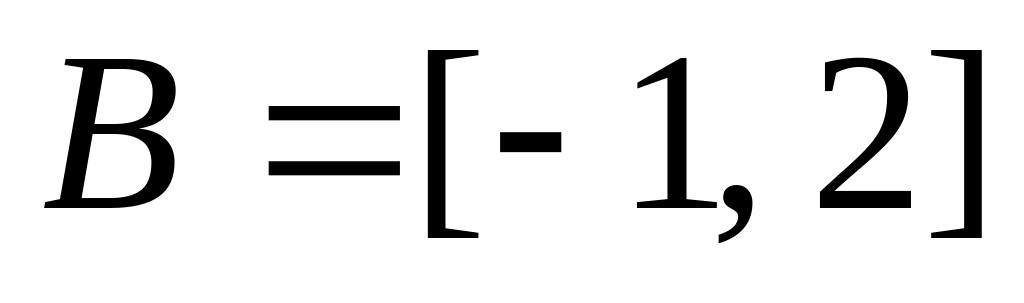 ,
,
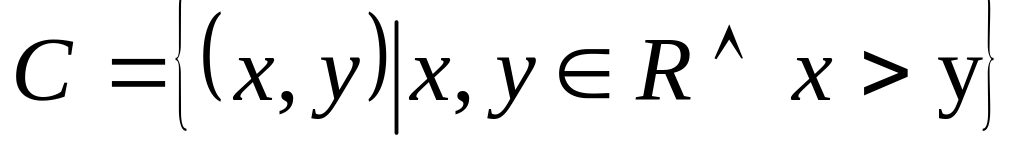 ;
;, где
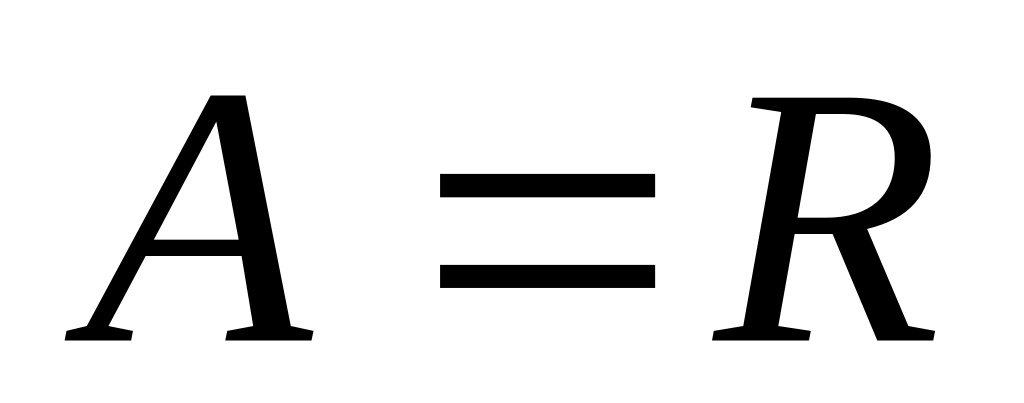 ,
,
 ,
,
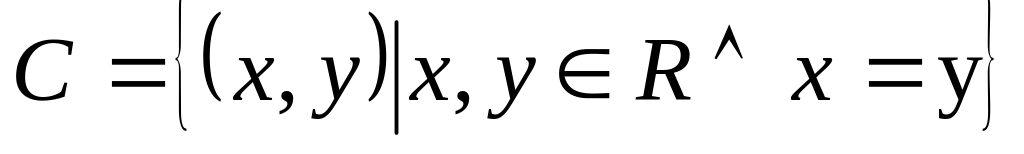 .
.
6. Дать
геометрическую интерпретацию множества
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
7. Каждое из следующих утверждений либо докажите, либо покажите с помощью контрпримера, что оно не всегда верно:
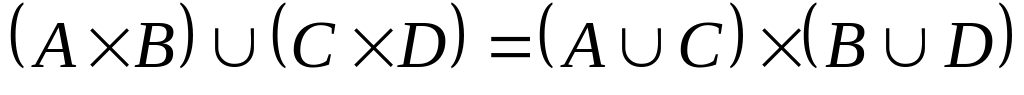 ;
;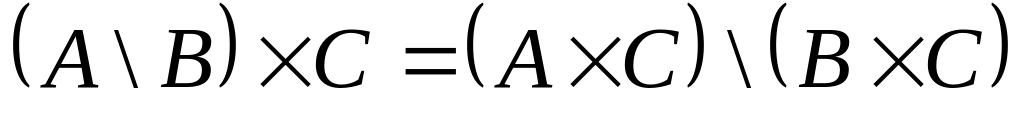 ;
;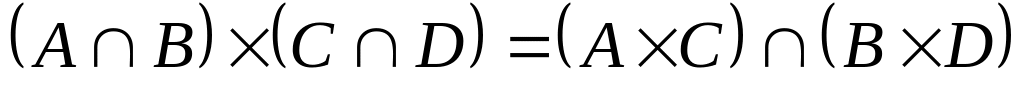 ;
; ;
; ;
;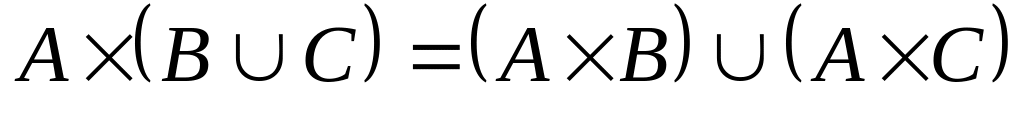 ;
; ;
;
8. Перечислите все элементы бинарного отношения R, постройте его граф и график:
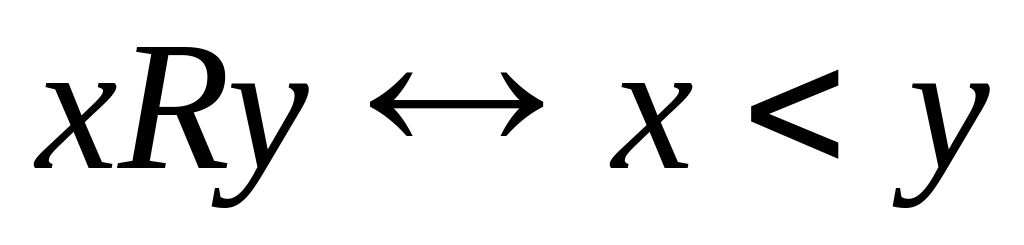 на множестве
на множестве
 ;
; на множестве
на множестве
 ;
;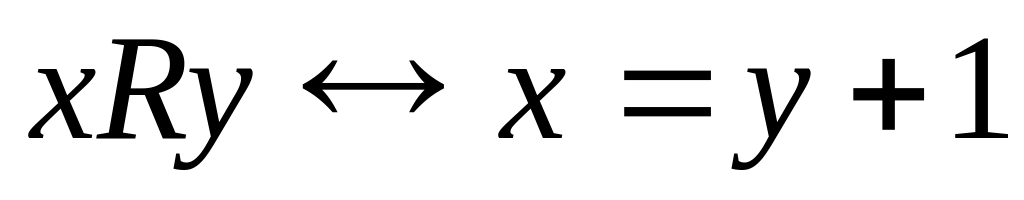 на множестве
на множестве
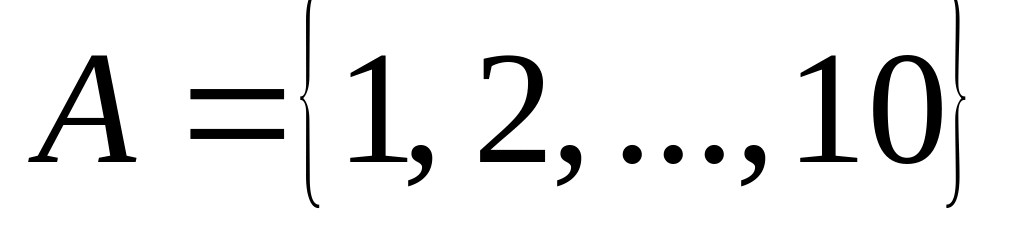 .
.
9. Перечислите все элементы бинарного отношения R. Определите, какими свойствами обладает данное отношение. Постройте граф и график.
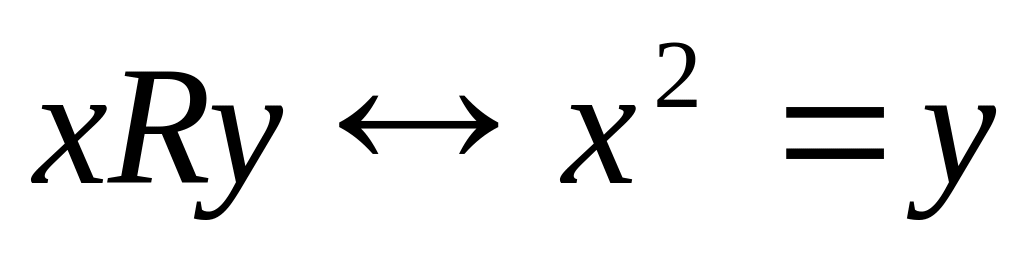 на множестве
на множестве
 ;
; на множестве
на множестве
 ;
;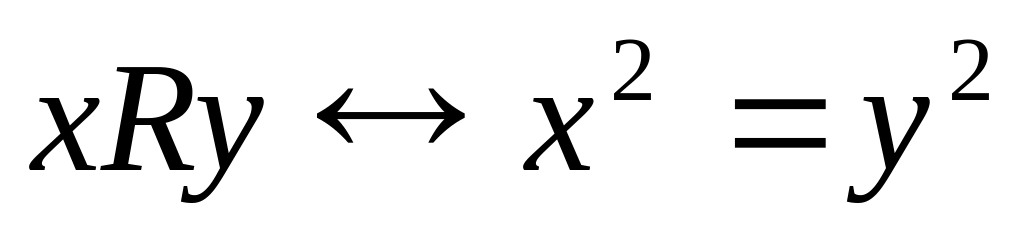 на множестве
на множестве
 ;
;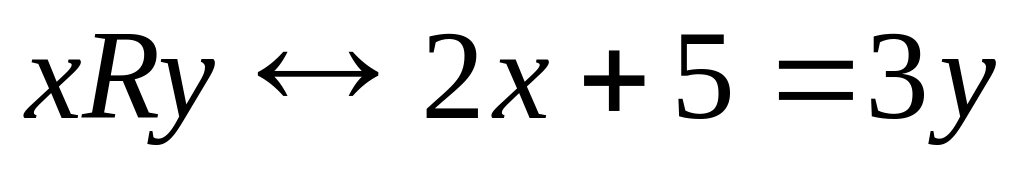 на множестве
на множестве
 ;
; на множестве
на множестве
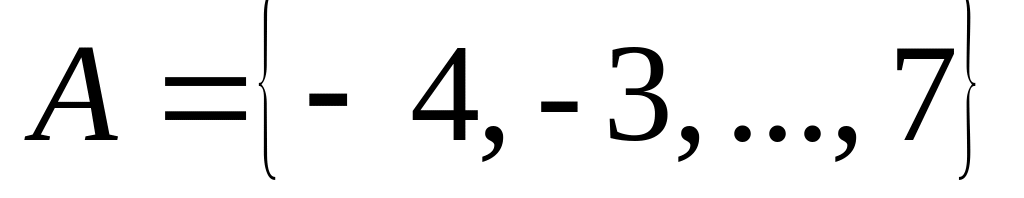 ;
;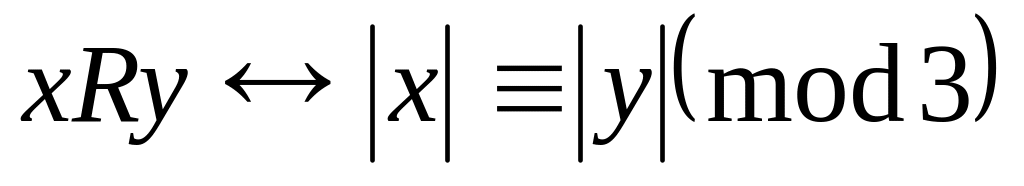 на множестве
на множестве
 ;
; на множестве
на множестве
 ;
; на множестве
на множестве
 ;
;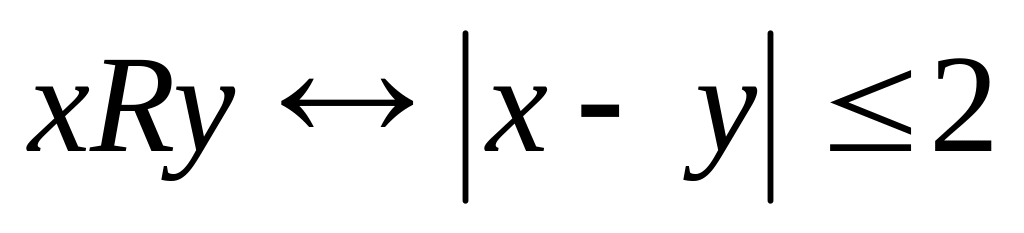 на множестве
на множестве
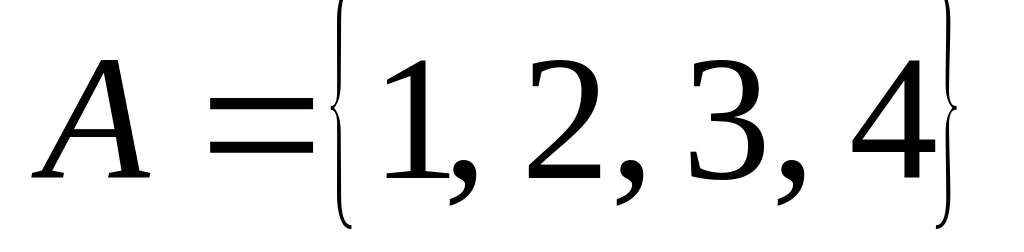 ;
;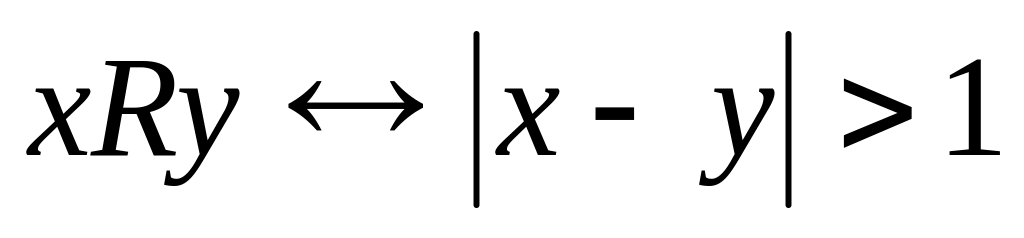 на множестве
.
на множестве
.
10. Бинарное отношение задано своим множеством, определите его свойства, постройте граф и график.
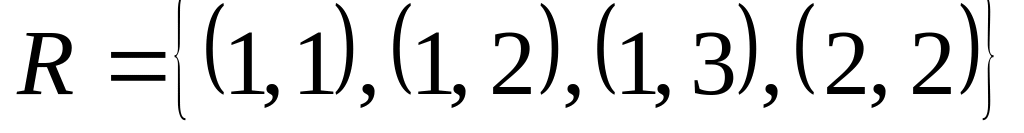 на множестве
на множестве
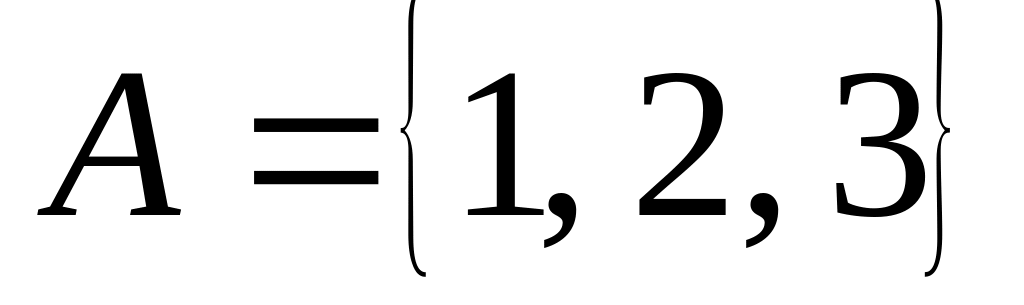 ;
;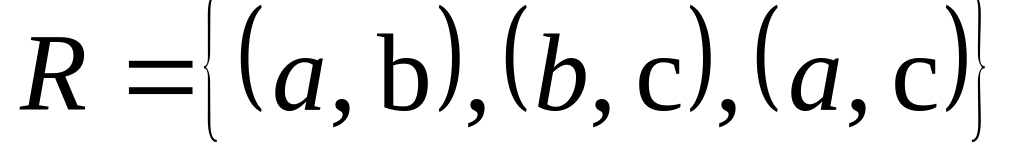 на множестве
;
на множестве
; на множестве
на множестве
 ;
; на множестве
;
на множестве
;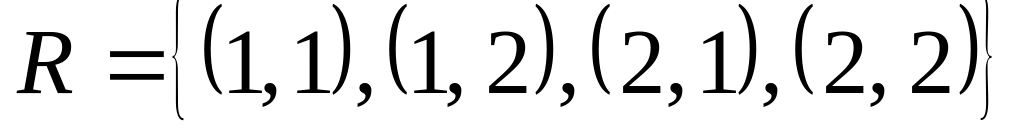 на множестве
;
на множестве
; на множестве
.
на множестве
.
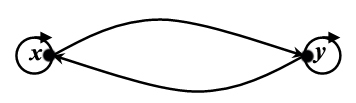
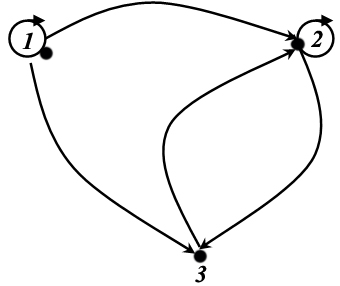
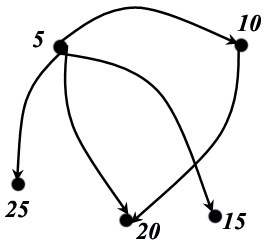
11. Бинарное отношение задано своим графом. Определите, на каком множестве задано отношение, выпишите множество бинарного отношения, определите его свойства.
|
|
|
|
|
|
12. Для каждого из следующих бинарных отношений, определенных на множестве целых чисел Z, выясните, какими свойствами оно обладает и какими не обладает. Является ли отношение отношением эквиваленции или отношением порядка.
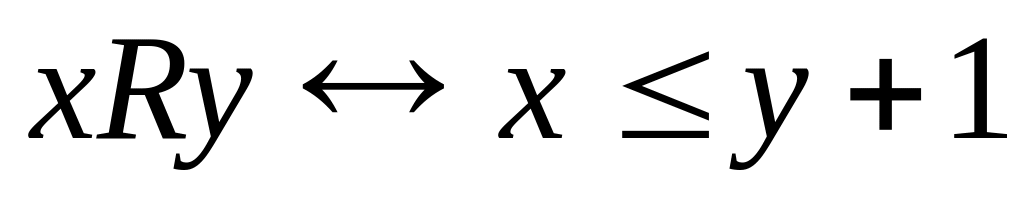 ;
; ;
;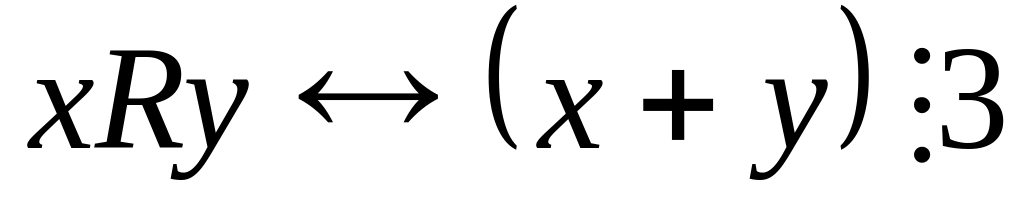 ;
;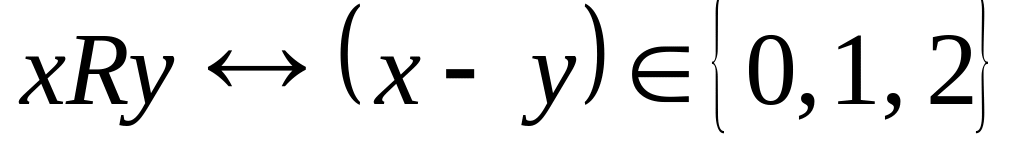 .
.
13. Для каждого из следующих бинарных отношений, определенных на множестве действительных чисел R, выясните, какими свойствами оно обладает и какими не обладает. Является ли отношение отношением эквиваленции или отношением порядка. Постройте график.
;
;
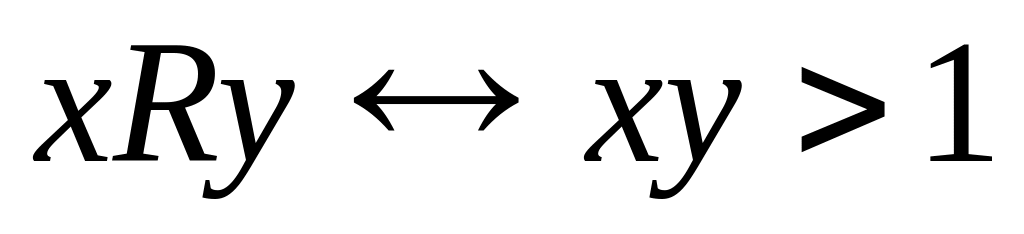 ;
;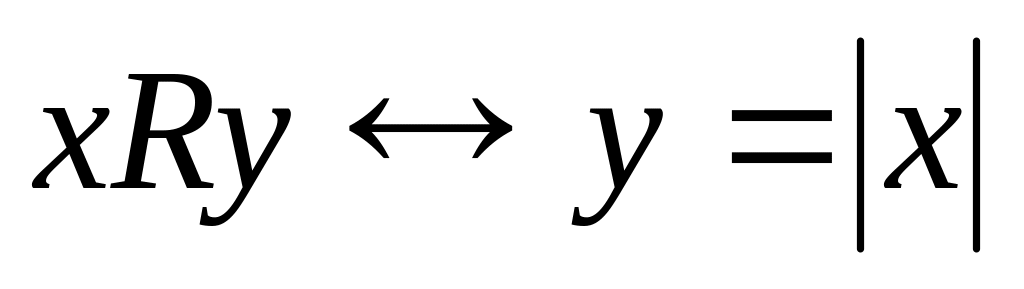 ;
; .
.
14. Определите свойства отношений, определенных на множестве P(Z). (P(Z) – множество всевозможных подмножеств множества целых чисел).
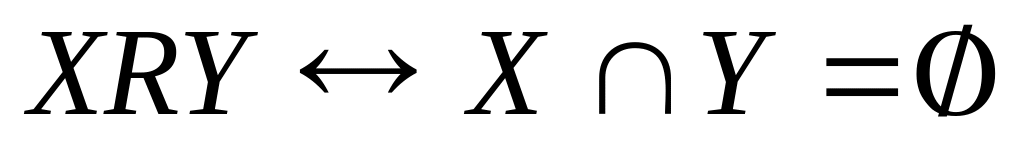 ;
; ;
;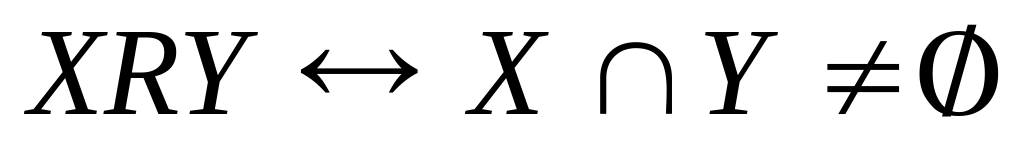 ;
;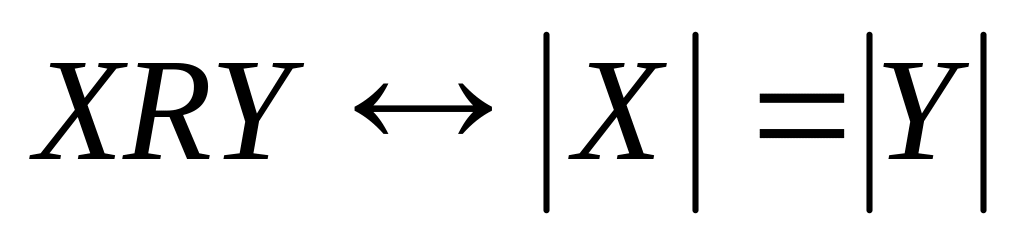 ;
; ;
;
15. Для каждого из следующих бинарных отношений, определенных на множестве всех прямых плоскости, выясните, какими свойствами оно обладает и какими не обладает. Является ли отношение отношением эквиваленции или отношением порядка.
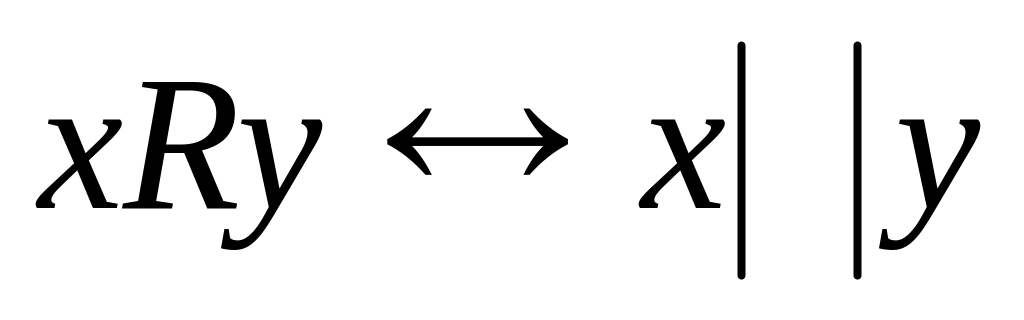 ;
; ;
;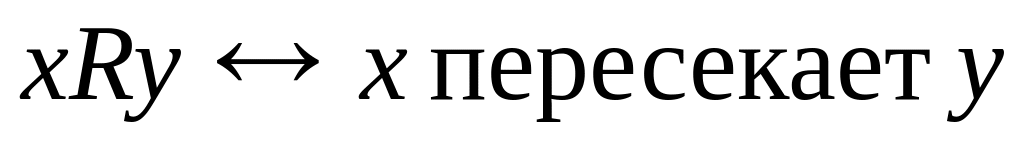 .
.
16. Докажите, что каждое из следующих отношений является отношением эквивалентности, и найдите классы эквивалентности.
 на множестве
на множестве
 ;
;на множестве P(A), где (P(А) – множество всевозможных подмножеств множества А);
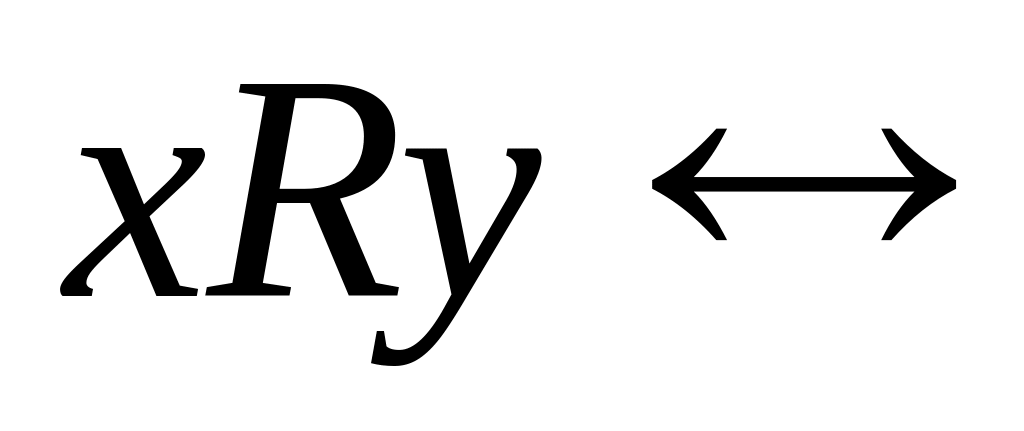 последние цифры в десятичной записи
чисел x и y
совпадают, на множестве Z;
последние цифры в десятичной записи
чисел x и y
совпадают, на множестве Z; на множестве
на множестве
 ;
;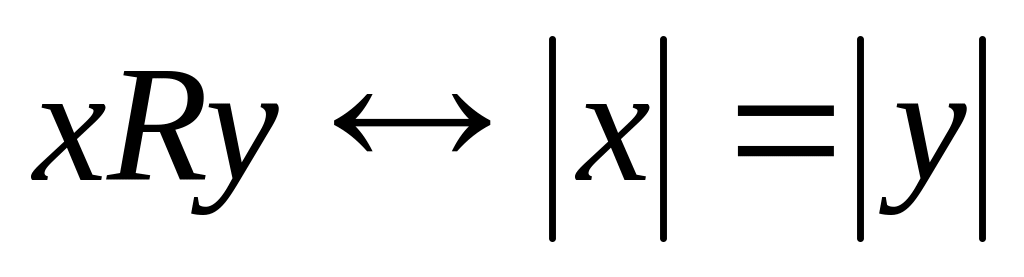 на множестве Z.
на множестве Z.
17. Даны
бинарные отношения
![]() и
и
![]() .
Найти
.
Найти
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
 ,
,
 ;
;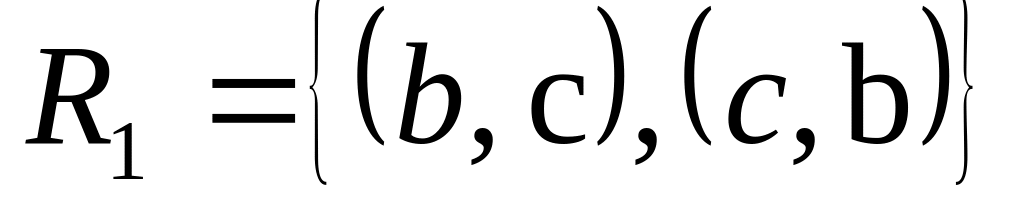 ,
,
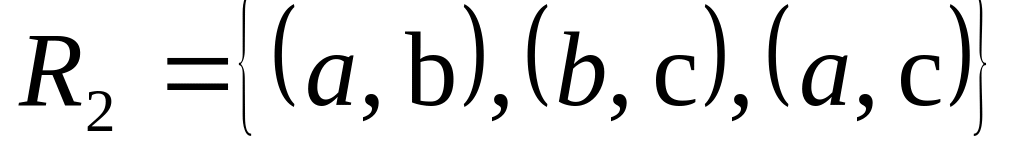 ;
;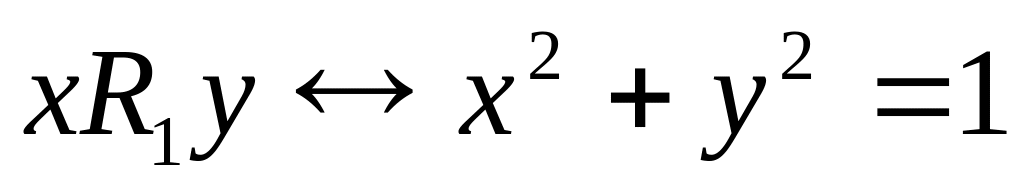 ,
,
 ,
и
определены на множестве Z;
,
и
определены на множестве Z;,
 ,
и
определены на множестве R;
,
и
определены на множестве R;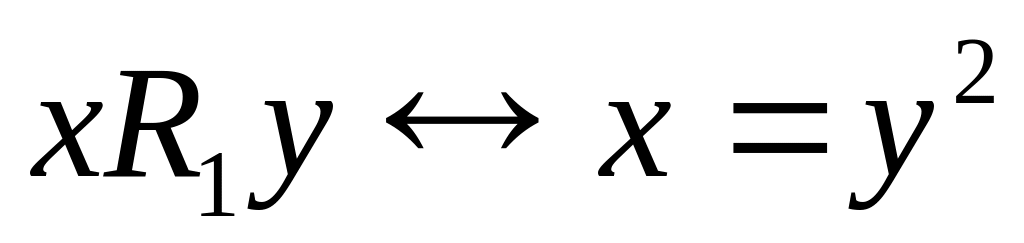 ,
,
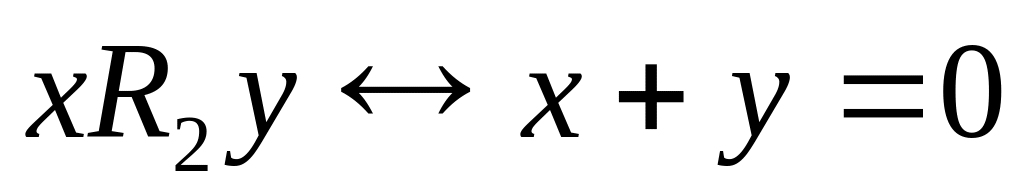 ,
и
определены на множестве R;
,
и
определены на множестве R; ,
,
и
определены на множестве R;
,
,
и
определены на множестве R;,
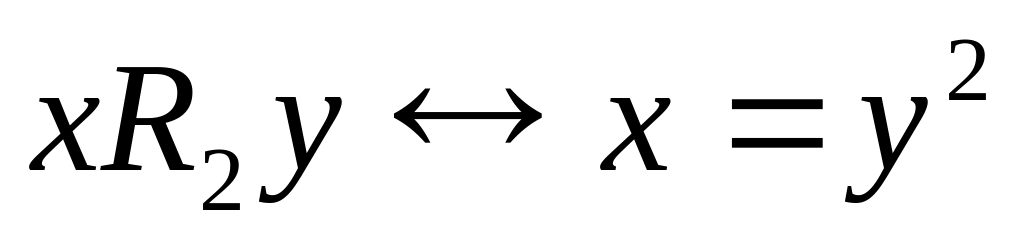 ,
и
определены на множестве R.
,
и
определены на множестве R.
18. Бинарные отношения определены на множестве всех прямых плоскости. Найдите инверсию для каждого отношения и композицию отношений.
;
;
.
19. Заданы отношения
![]() ,
,
![]() ,
,
![]() .
.
Найти
,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
20. Определите, является ли бинарное отношение функциональным (функцией). В случае положительного ответа установить его свойства: инъективное, сюрьективное, биективное; определите образ функционального отношения.
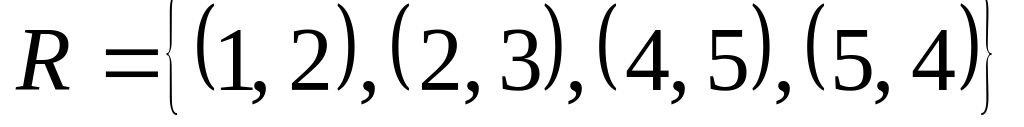 на множестве
на множестве
 ;
;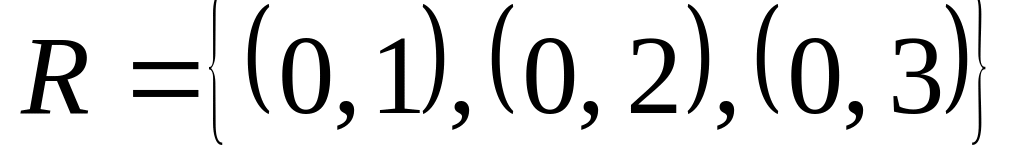 на множестве
на множестве
 ;
;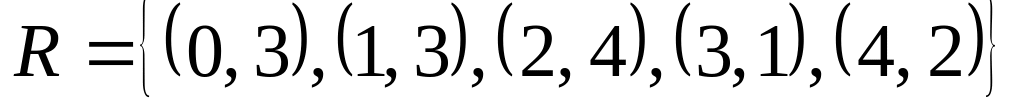 на множестве
;
на множестве
; на множестве
;
на множестве
; на множестве
на множестве
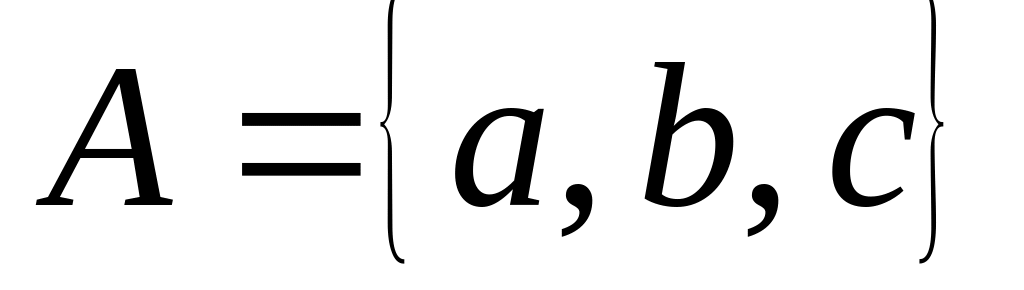 .
.
21. Определите, является ли бинарное отношение функциональным (функцией). В случае положительного ответа установить его свойства: инъективное, сюръективное, биективное; определите образ функционального отношения. Постройте график.
 на множестве R;
на множестве R;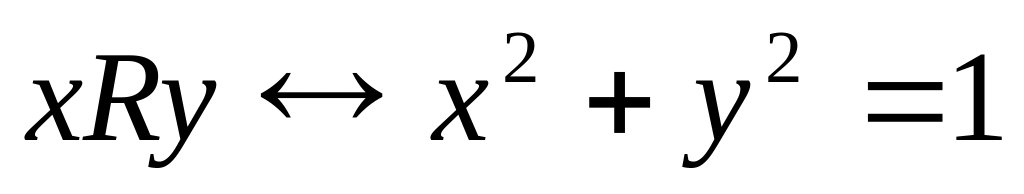 на множестве
на множестве
 ;
;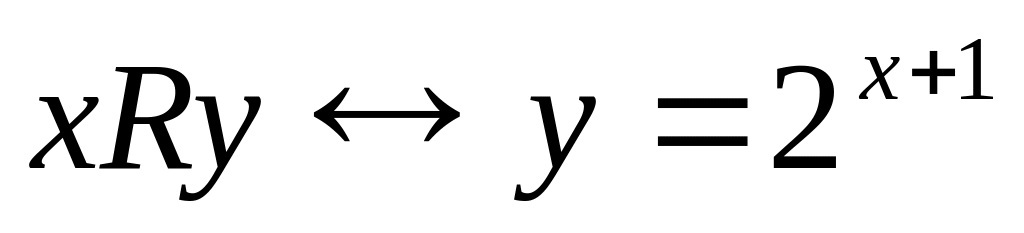 на множестве
на множестве
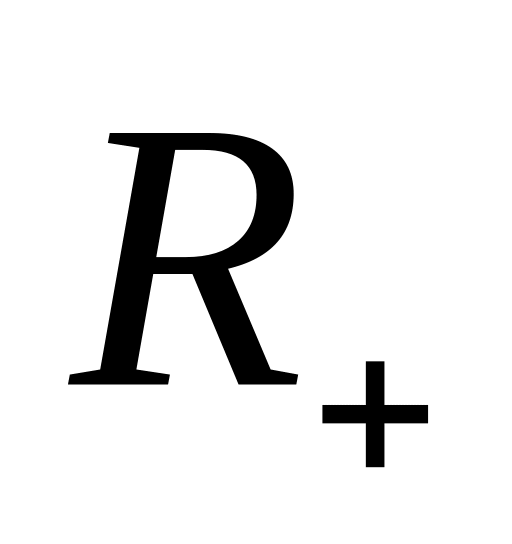 ;
; на множестве R;
на множестве R;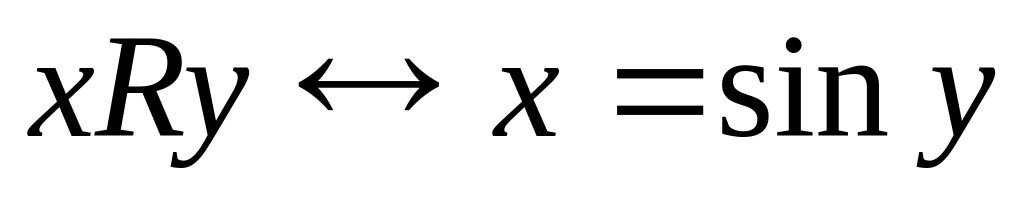 на множестве
.
на множестве
.
22. Для каждой из следующих пар множеств A и B выясните, сколько существует различных отображений из множества А в множество В. Сколько среди них инъекций, сюръекций, биекций?
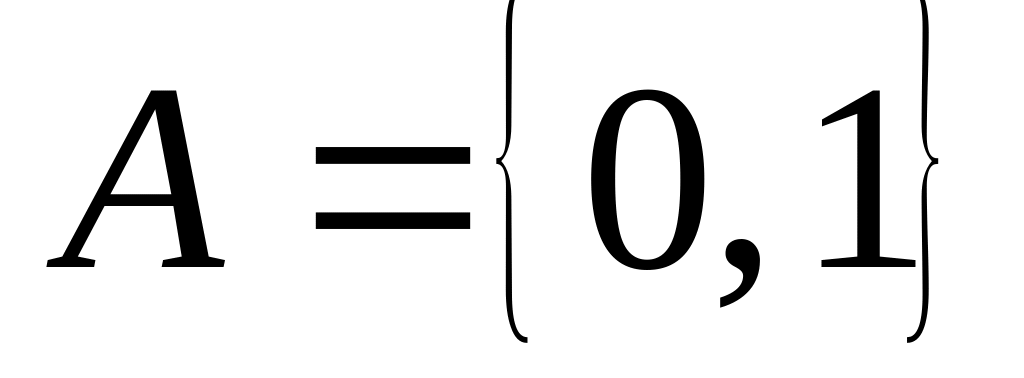 ,
;
,
;,
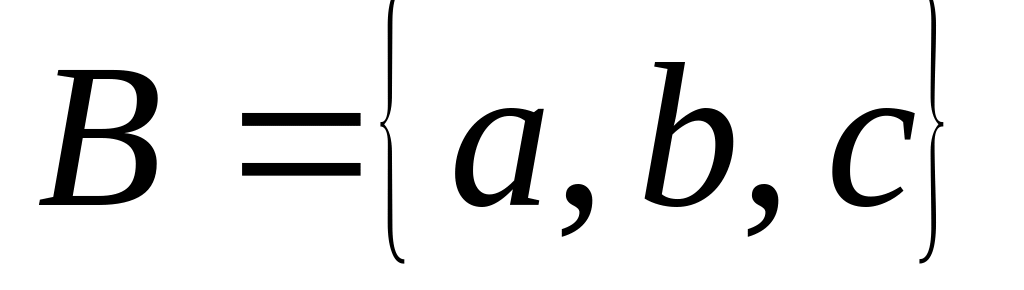 ;
;,
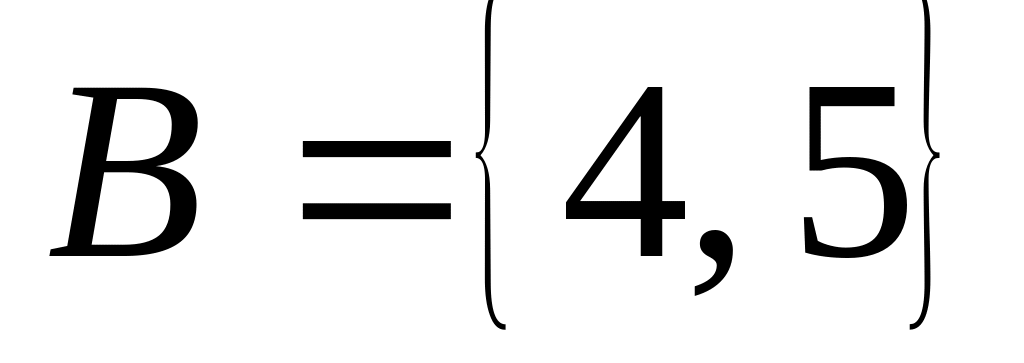 ;
; ,
,
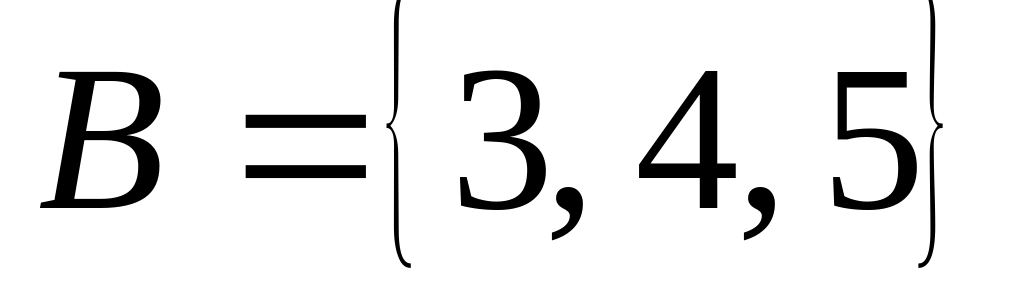 .
.
23. Для
следующих функций f и g
найдите композиции
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
 ,
,
 ;
; ,
,
 ;
; ,
,
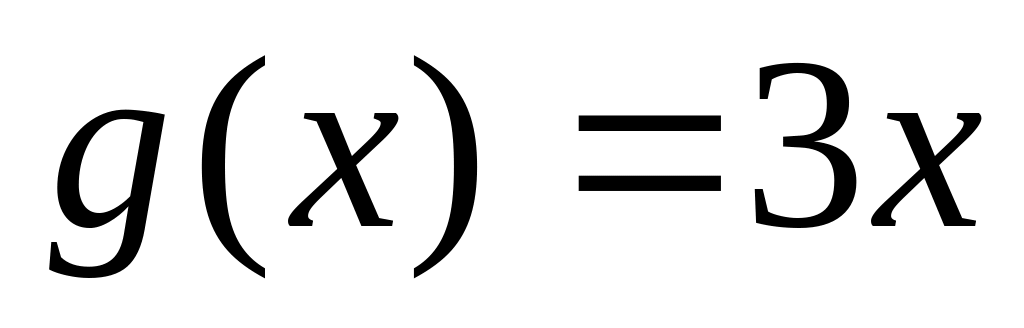 .
.
24. Следующие функции представьте виде композиции нескольких более простых функций:
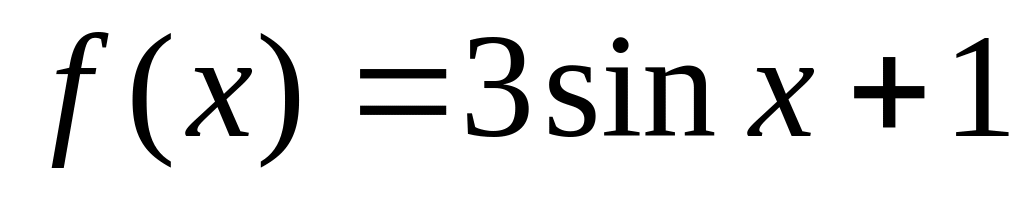 ;
;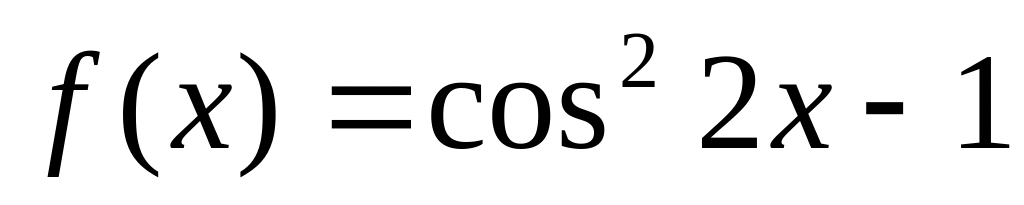 ;
;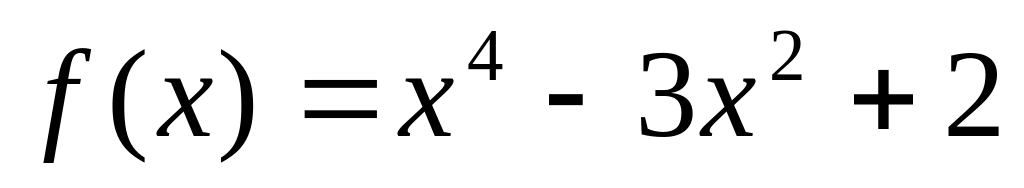 ;
;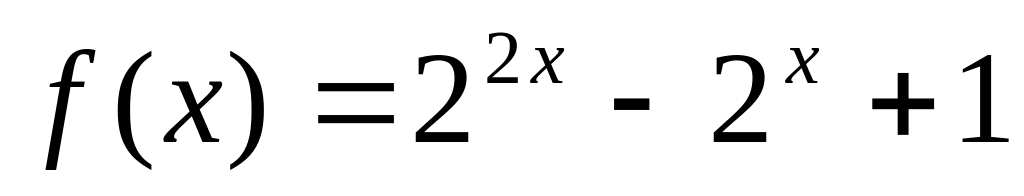 .
.
25. Докажите, что следующие пары функций являются взаимообратными:
 ,
,
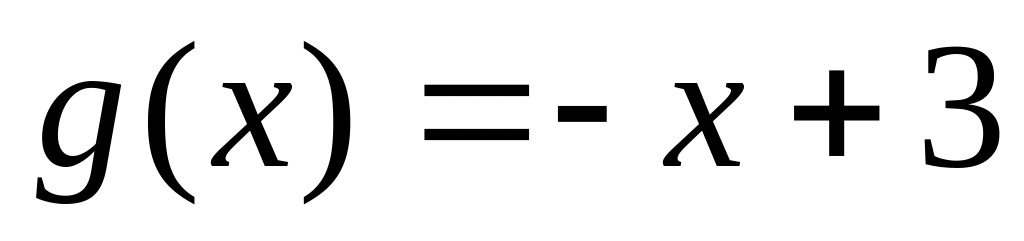 ;
;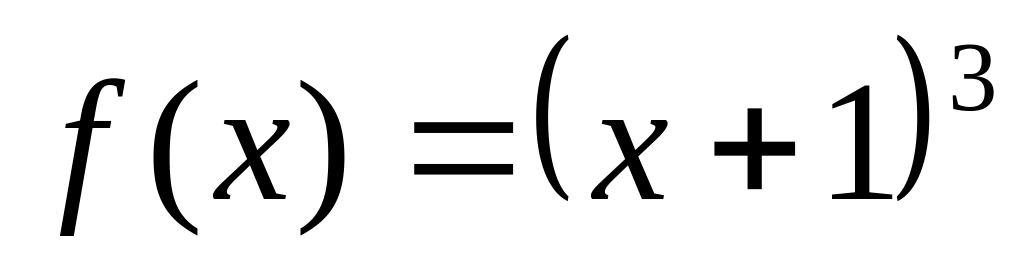 ,
,
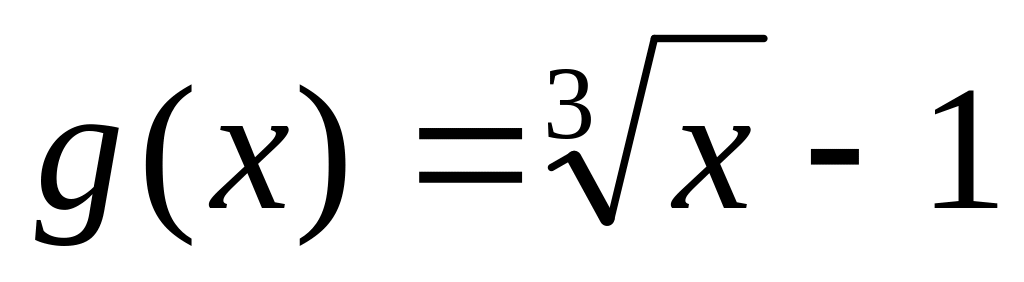 ;
; ,
,
 .
.
26. Для следующих функций, определенных на множестве действительных чисел, найдите обратные.
;
;
;
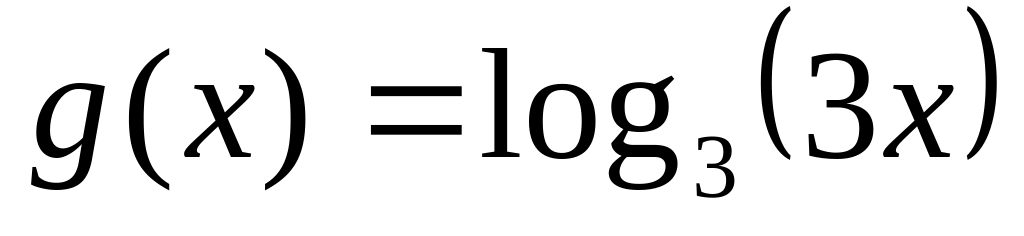
 ;
;;
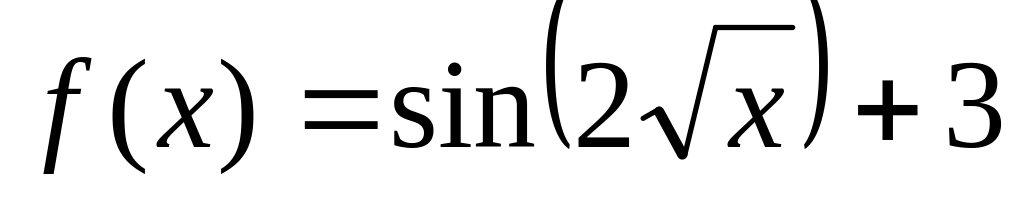 .
.