
- •Элементы математической логики
- •, Если ;
- •, Если , , ;
- •, Если , .
- •Теория множеств
- •26. Решите задачу:
- •27. Решите задачу:
- •28. Решите задачу:
- •Бинарные отношения
- •Метод математической индукции
- •Комбинаторика
- •Типовые контрольные работы
- •Вариант 1
- •Вариант 2
- •Вариант 1
- •Вариант 2
- •Вариант 1
- •Вариант 2
- •Используемая литература
Элементы математической логики
Основные понятия: Высказывания, логические операции над ними и их свойства, формул логики высказываний, эквивалентность формул логики высказываний, тавтология, противоречие, табличный и аналитический способы доказательства свойств логических операций, законы логики. Предикаты, область истинности предикатов, логическое следование предикатов, равносильность предикатов, кванторы общности и существования, построение отрицаний высказываний, теоремы, структура теоремы, виды теоремы.
1. Какие из следующих выражений являются высказываниями? Для высказываний определите их истинностное значение.
Солнце вращается вокруг Земли
В романе Толстого «Война и мир» 14563970 слов.
Да здравствует солнце, да скроется тьма!
Студент 1 курса.

Число 3 удовлетворяет неравенству

Натуральное число x больше 8.
2. Определите истинностное значение следующих высказываний.
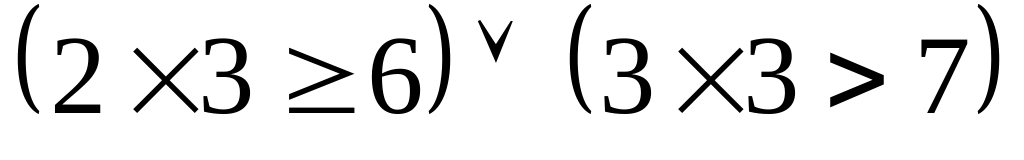

Если 12 делится на 6, то 12 делится на 3.
Если 15 делится на 6, то 15 делится на 3.
15 делится на 6 тогда и только тогда, когда 15 делится на 3.
12 делится на 6 тогда и только тогда, когда 12 делится на 3.
Неверно, что
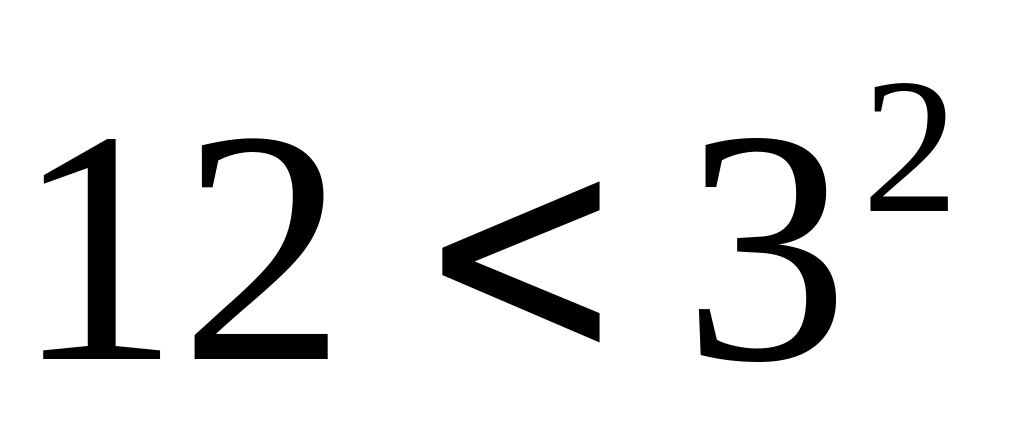


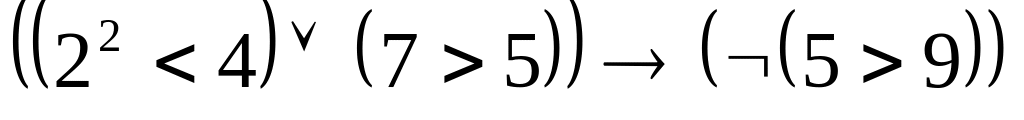

Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник – ромб.
3. Определите значение истинности высказывания А, если следующие высказывания истинны:
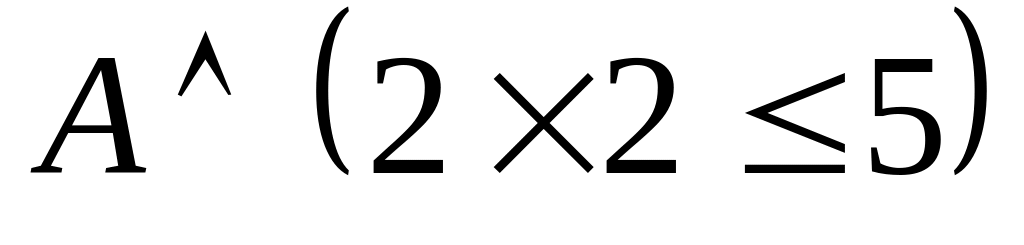

Если А, то 4 – нечетное число,
А тогда и только тогда, когда 22=5.
4. Определите значение истинности высказывания А, если следующие высказывания ложны:

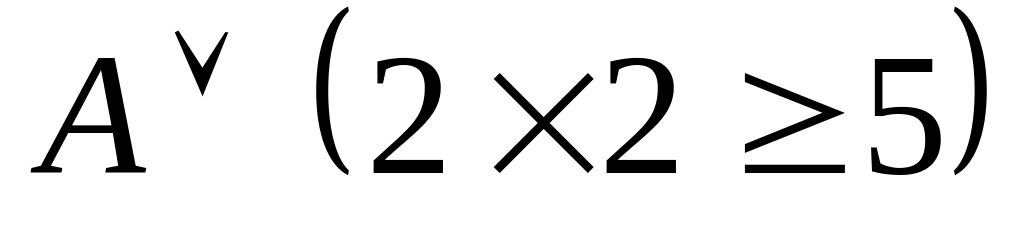
Если 2 – четное число, то А,
Если А, то 4 – четное число,
А тогда и только тогда, когда 22=4,
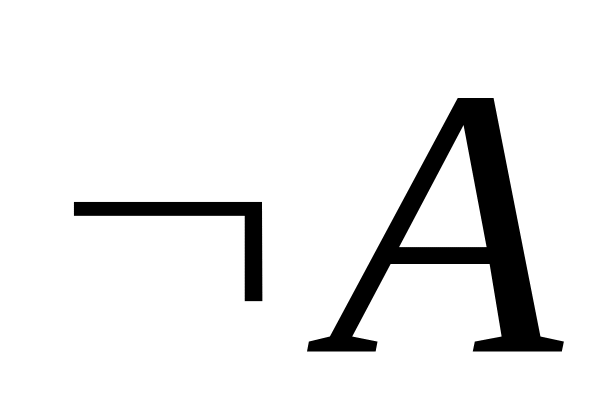 .
.
5. Какие из приведенных имен удовлетворяют логическим условиям:
¬ (последняя буква гласная → первая буква согласная) /\ вторая буква согласная
(Первая буква гласная Последняя буква согласная) → ¬(Третья буква согласная)?
Первая буква гласная Четвертая буква согласная В слове четыре буквы?
1) ИРИНА; 2) АРТЕМ; 3) СТЕПАН; 4) МАРИЯ
6. Пусть p – высказывание «сегодня ясно», q – «сегодня идет дождь», r – «сегодня идет снег», s – «вчера было пасмурно». Переведите на обычный язык следующие предложения:
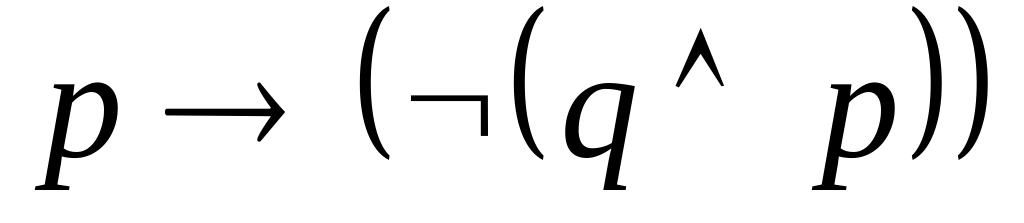 ,
, ,
,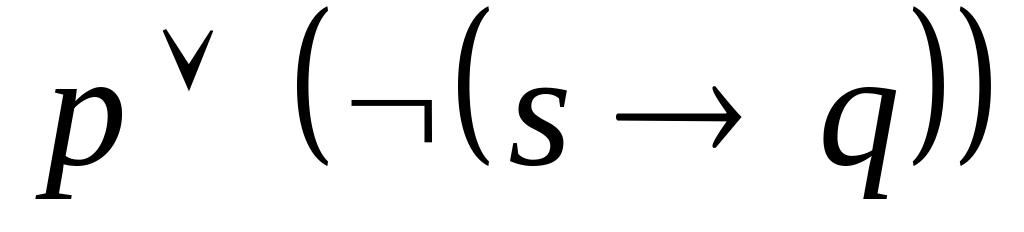 ,
, .
.
7. Заполните истинностную таблицу для каждой из следующих формул логики высказываний:
 ,
, ,
, ,
, ,
,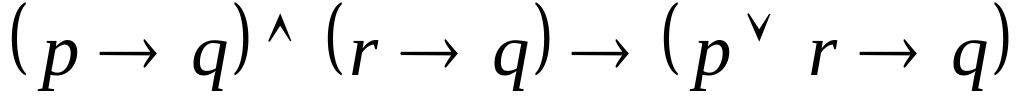 ,
,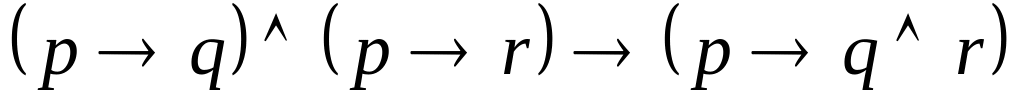 ,
, ,
, ,
,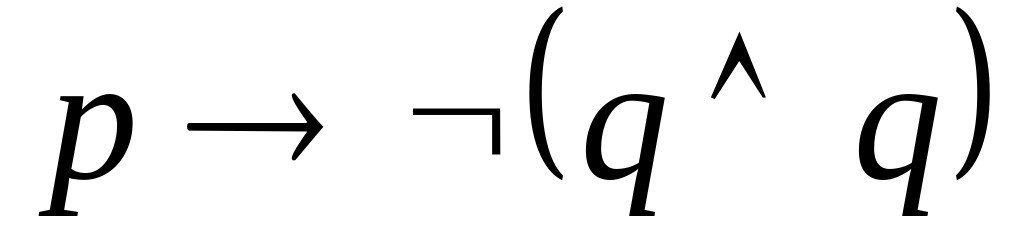 ,
,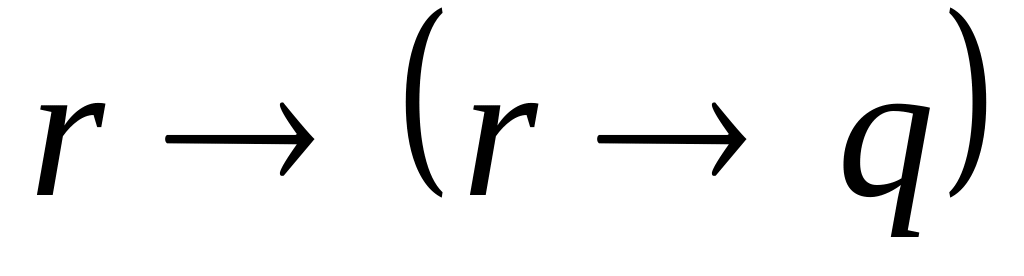 ,
,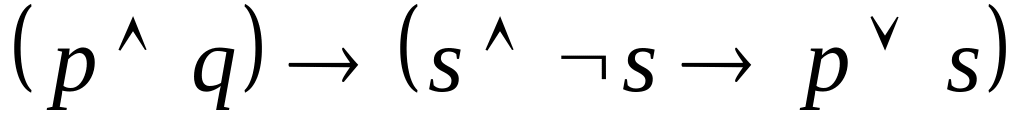 .
.
8. Что можно сказать об истинностном значении высказывания (|p| - истинностное значение p)
 ,
если
,
если
 ;
;, Если ;
, Если , , ;
, Если , .
9. Какие из следующих формул логики высказываний являются тавтологиями, противоречиями, не являются ни тем ни другим
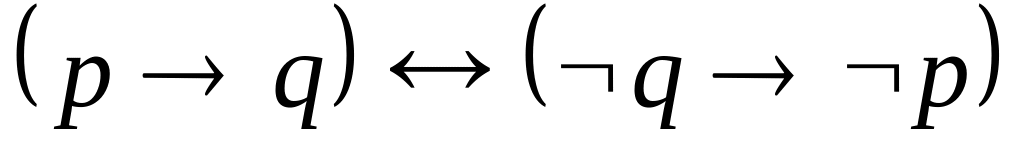 ,
, ,
,,
 ,
,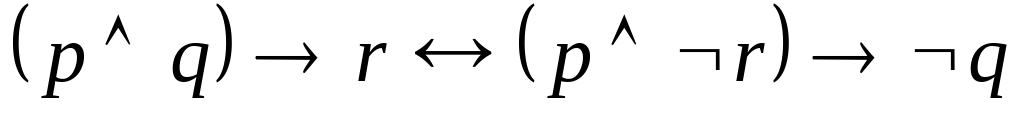 ,
,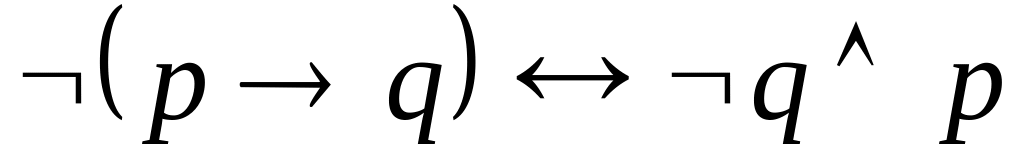 ,
, ,
, ,
,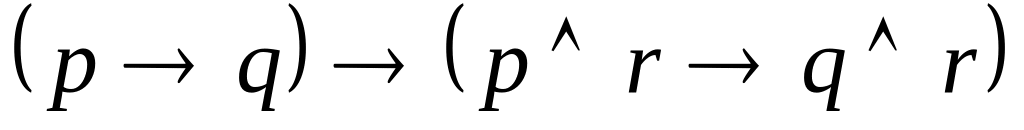 ,
, ,
, ,
,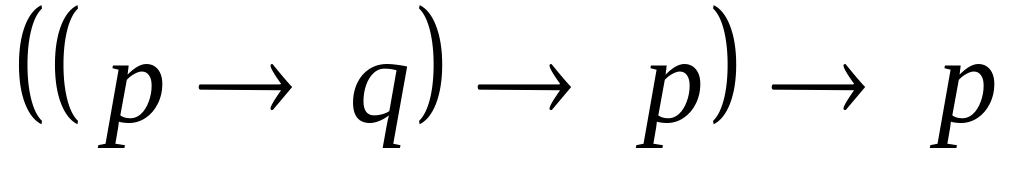 .
.
10. Решите задачу:
На вопрос: «Кто из трех студентов изучал логику?» - был получен верный ответ: «Если изучал первый, то изучал и третий, но неверно, что если изучал второй, то изучал и третий». Кто изучал логику?
11. Определите, кто из четырех студентов сдал экзамен, если известно, что выполнены следующие условия:
Если первый сдал, то и второй сдал.
Если второй сдал, то третий сдал или первый не сдал.
Если четвертый не сдал, то первый сдал, а третий не сдал.
Если четвертый сдал, то и первый сдал.
12. Докажите эквивалентность формул логики высказываний:
 ,
, ,
,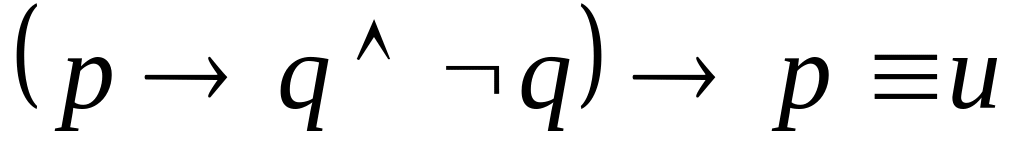 ,
, ,
,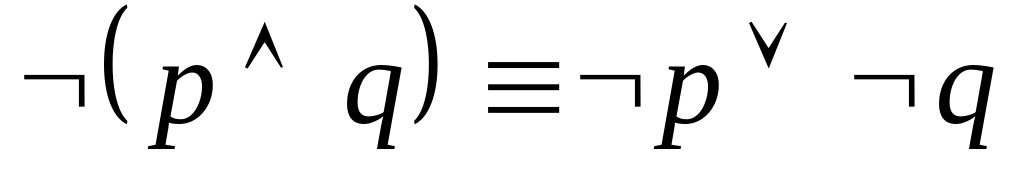 ,
, ,
, ,
,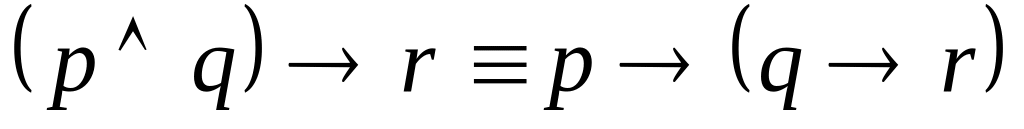 ,
, .
.
13. Упростите формулы логики высказываний, используя логические законы
 ;
; .
.
14. Сколько различных решений имеет уравнение
,
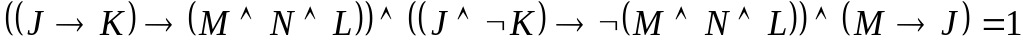
 .
.
15. Среди следующих предложений укажите высказывания, предикаты и те предложения, которые не являются ни тем, ни другим:
квадрат есть прямоугольник с равными сторонами;
прямоугольником называют четырехугольник, у которого все углы прямые;
если целое число k делится на 8, то k делится на 12;
если целое число k делится на 4, то k делится на 2;
каждое целое число, делящееся на 4, делится на 2;
каждое целое число, делящееся на 8, делится на 12;
x – столица России;
 ;
;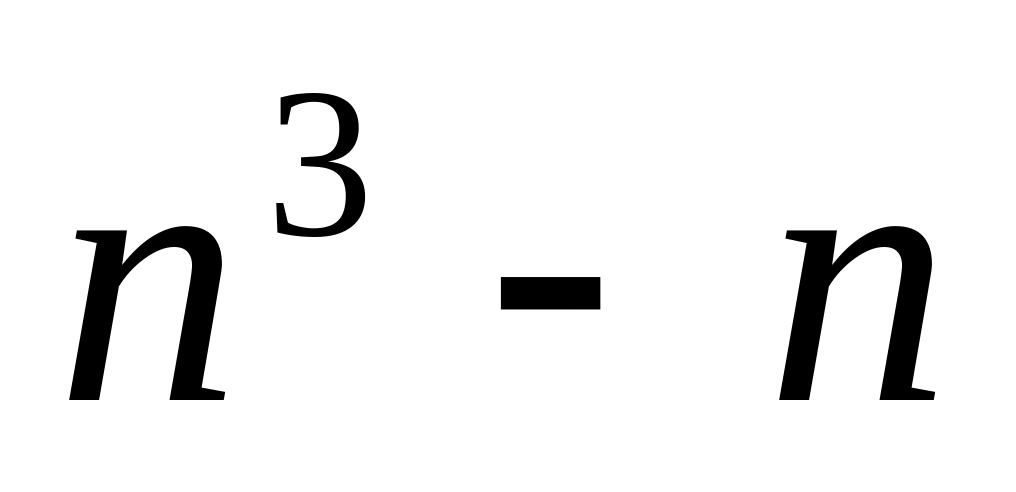 делится на 3;
делится на 3; ;
; ;
;существует такое целое число x, что
 и
и
 ;
;число 12 можно представить в виде суммы
 ,
где
,
где
 - некоторые простые числа;
- некоторые простые числа;x делится на y;
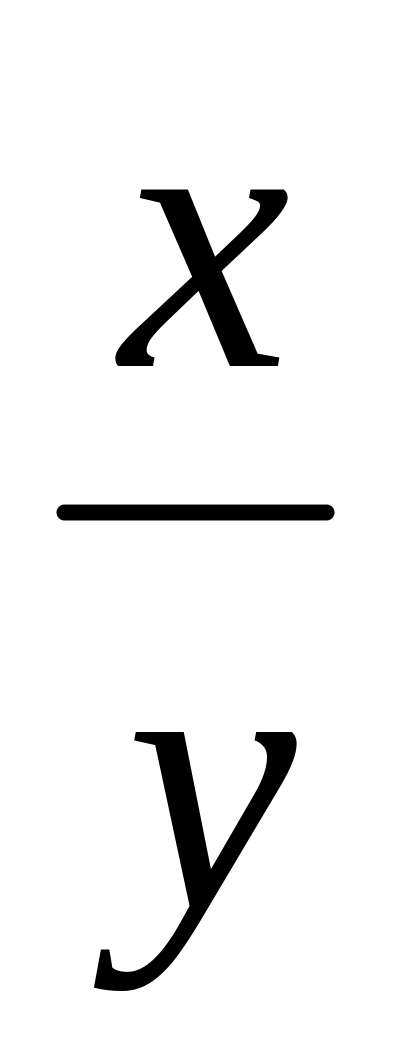 ;
; .
.
16. Найти
области истинности предикатов
![]() и
и
![]() .
Установить, равносильны ли предикаты
или является один из них логическим
следствием другого:
.
Установить, равносильны ли предикаты
или является один из них логическим
следствием другого:
 и
и
 ,
,
 ;
;и
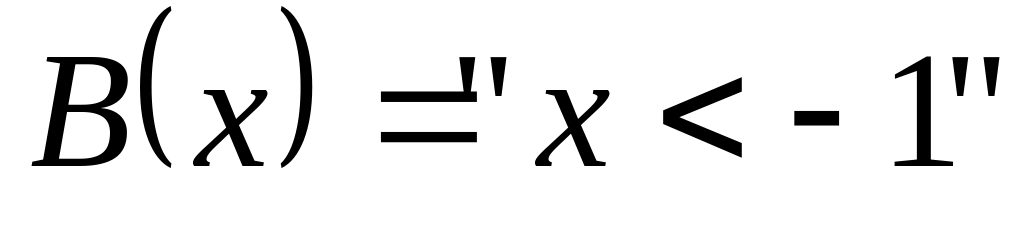 ,
;
,
;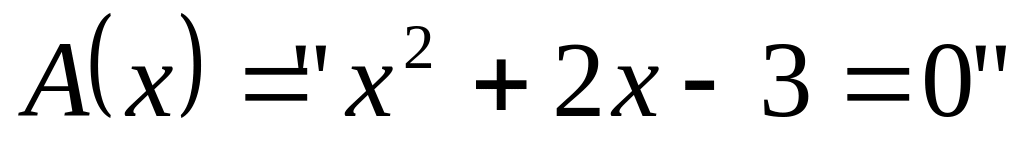 и
и
 ,
,
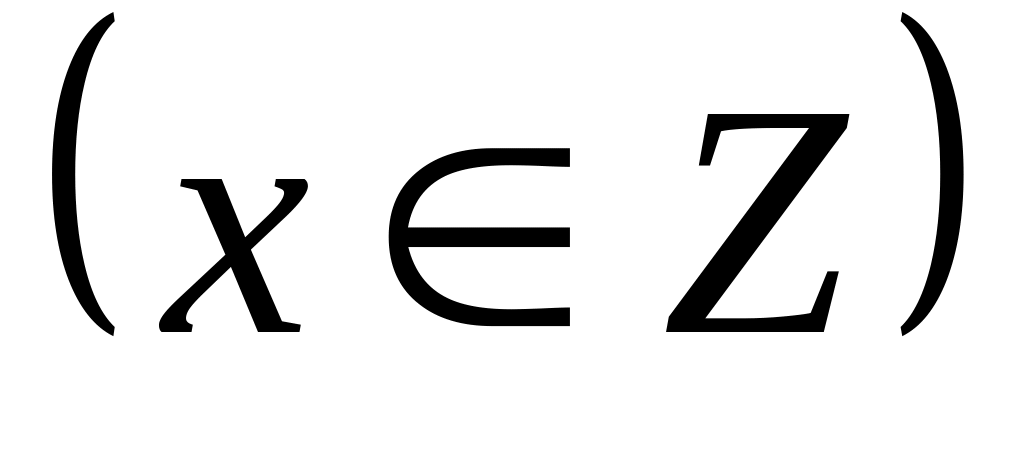 ;
;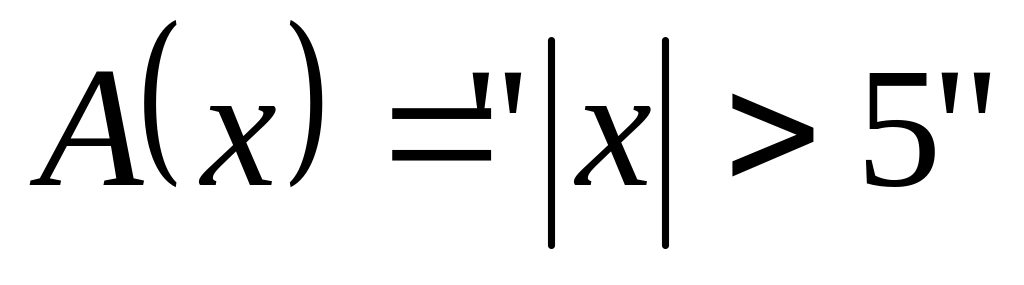 и
и
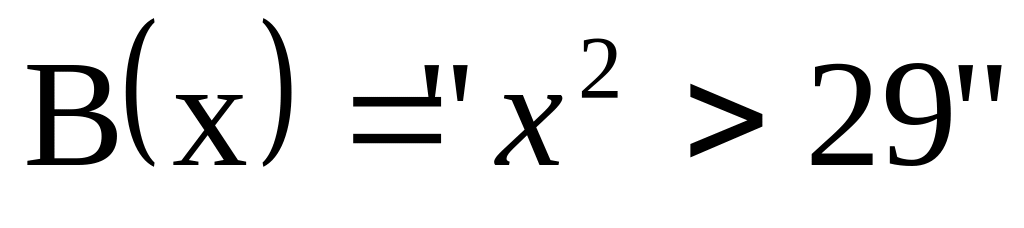 ,
;
,
;и
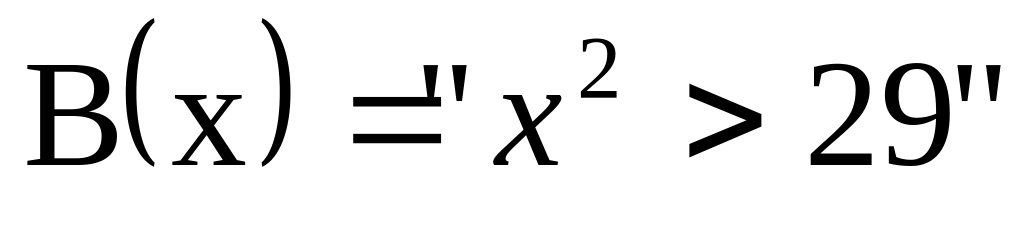 ,
;
,
;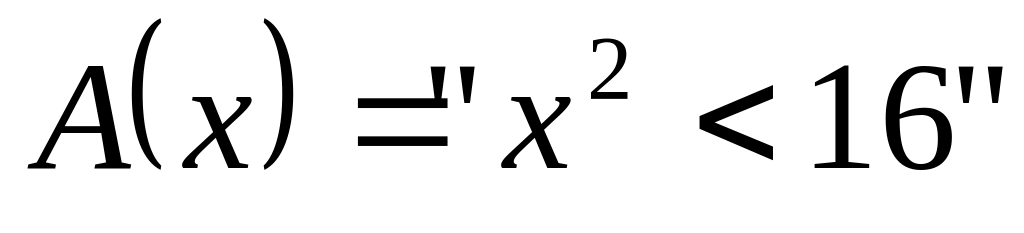 и
и
 ,
;
,
;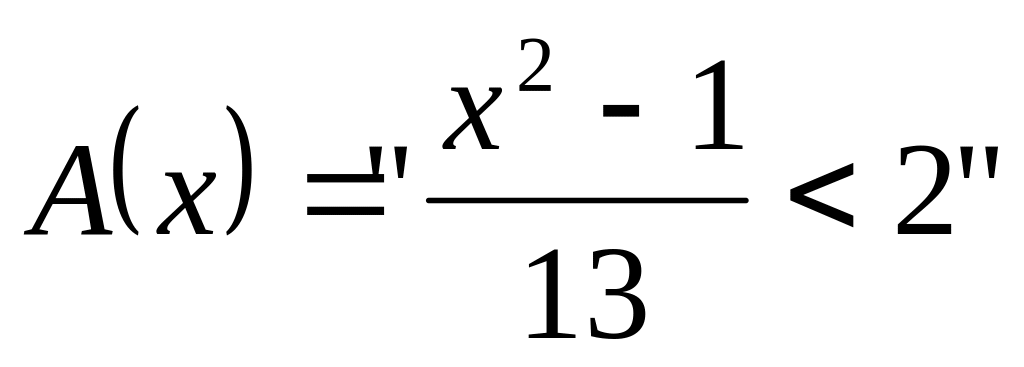 и
,
;
и
,
;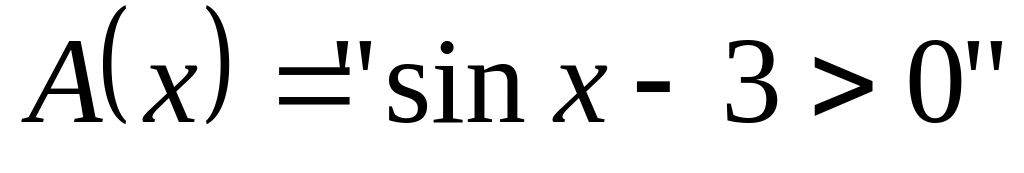 и
и
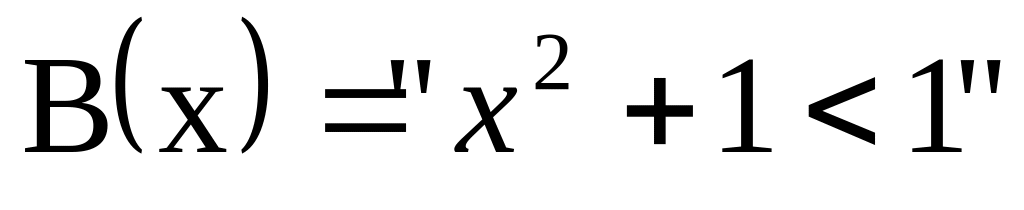 ,
;
,
; «x – четное число» и
=«число x делится на 6»,
;
«x – четное число» и
=«число x делится на 6»,
;«x – четное число» и =«число x делится на 3», ;
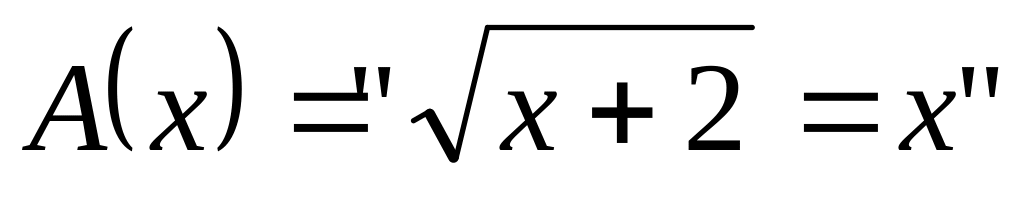 и
и
 ,
.
,
.
17. Запишите следующие высказывания в виде формул с кванторами, предварительно введя обозначения для используемых предикатов:
Некоторые реки впадают в Каспийское море.
Все люди знают, что Земля круглая.
По крайней мере, одно целое число делится на 8.
Не все птицы умеют летать.
Ни одна собака не умеет мяукать.
Кто хочет, тот добьется.
Если целое число делится на 4, то оно делится на 2.
18. Пусть P(x,y) – это предикат «официант x обслуживает стол y». Переведите на обычный язык следующие высказывания:
 ;
;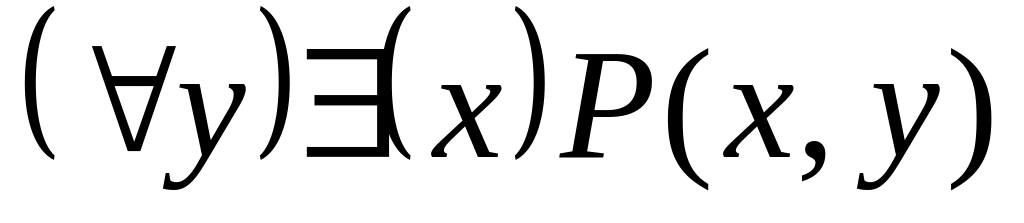 ;
;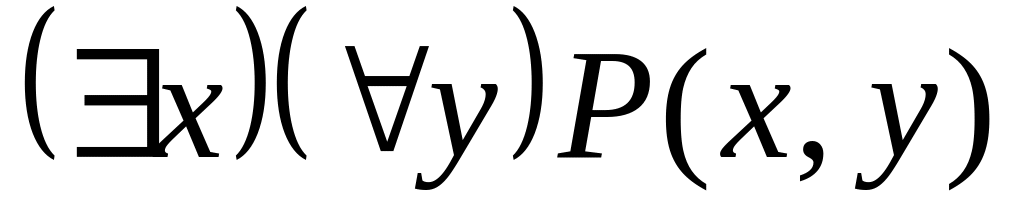 ;
; ;
; ;
;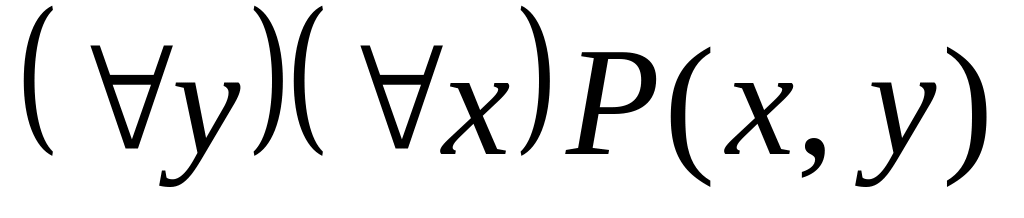 ;
; ;
; .
.
19.Через обозначен предикат «число x четно». Прочтите следующие утверждения и выясните, какие из них верны при всех значениях x и y.
 ;
; ;
;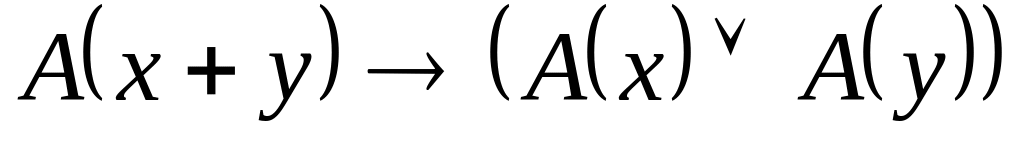 ;
;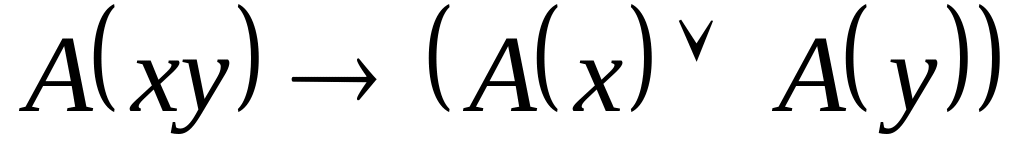 ;
; ;
;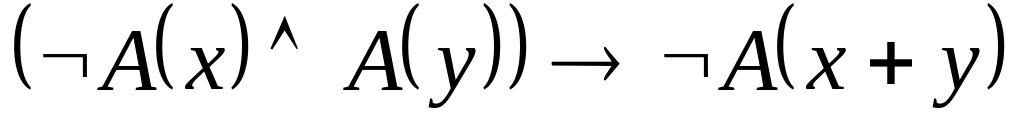 ;
;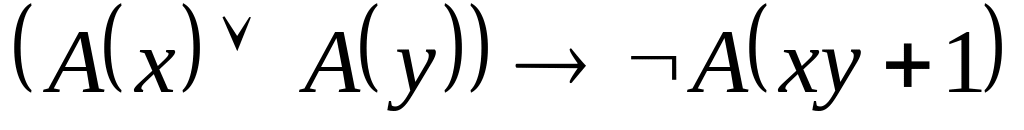 .
.
20. Пусть P(x) – предикат «x – простое число», Е(x) –«x – четное число», D(x,y) –«x делится на y», I(x,y) – «x равно y». Переведите на обычный язык следующие высказывания, оцените их истинность и постройте отрицания.
P(7);
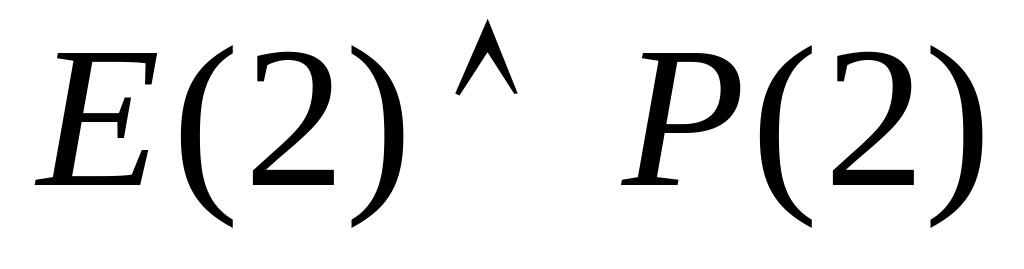 ;
;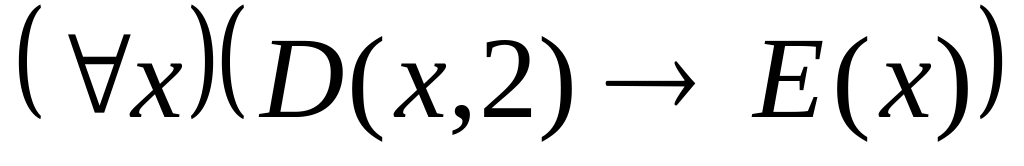 ;
; ;
;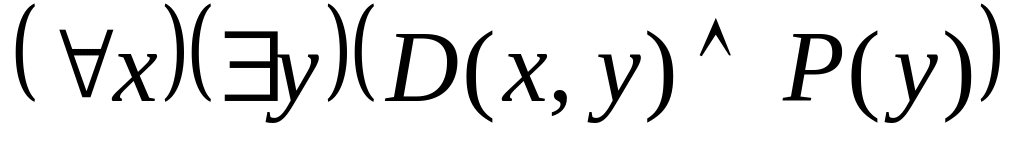 ;
;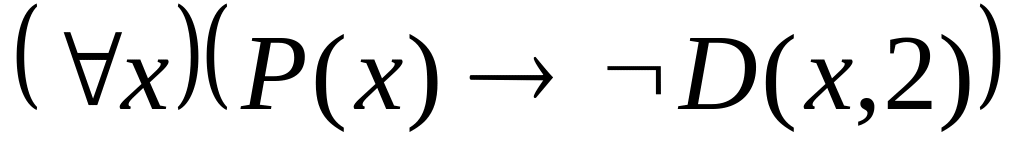 ;
;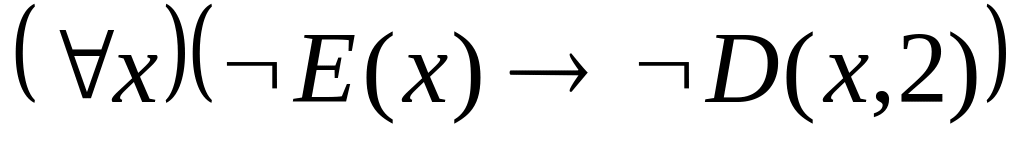 ;
;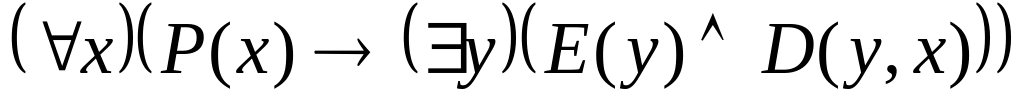 ;
; ;
;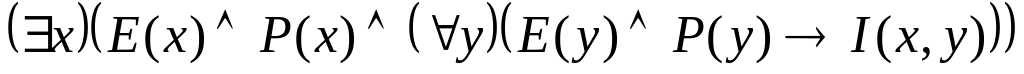 ;
; ;
;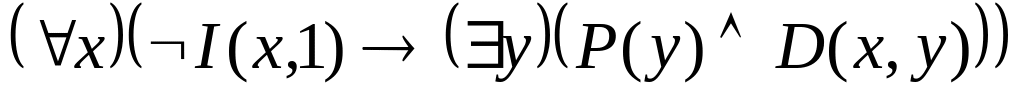 .
.
21. Запишите следующие высказывания о натуральных числах при помощи логических символов, используя следующие обозначения для предикатов: НОД(a,b)=1 – «a и b – взаимно простые числа», НОД(a,b)=d – «d – наибольший общий делитель чисел a и b» и обозначения из предыдущей задачи.
если x делится на y, y делится на z, то x делится на z;
если два простых числа делятся друг на друга, то они равны;
если число делится на два взаимно простых числа, то оно делится на их произведение;
если a и b делятся на c, то a+b и a-b делятся на c;
если a и b оба четные или оба нечетные, то a+b и a-b четные;
любое число делится на 6 тогда и только тогда, когда его квадрат делится на 6;
если НОД(a,b)=d, то a и b делятся на d иd делится на любой общий делитель a и b;
2 – наименьшее простое число;
простое число отличное от 2, нечетно;
два числа, делящиеся друг на друга, совпадают;
любое число отличное от 1, имеет хотя бы один простой делитель.
22. Для каждого из следующих утверждений сформулируйте обратное к нему, противоположное и противоположное к обратному утверждению:
квадратное уравнение имеет корни только в том случае, когда его дискриминант неотрицателен;
если дискриминант квадратного трехчлена равен нулю, то его корни совпадают;
сумма корней квадратного трехчлена
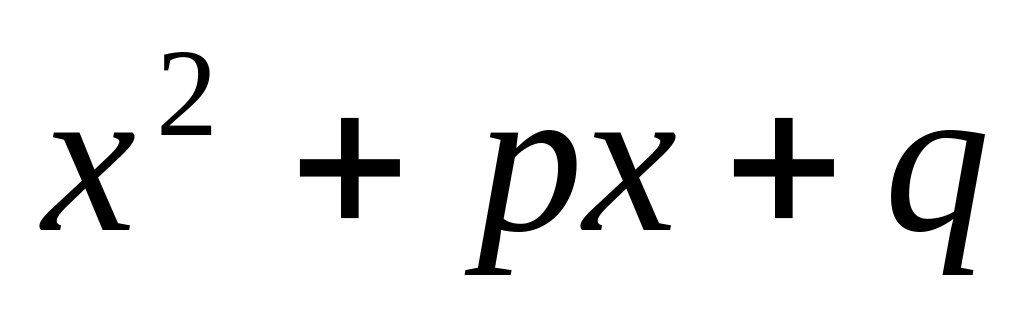 равна –p, а произведение
корней равно q;
равна –p, а произведение
корней равно q;диагонали ромба взаимно перпендикулярны;
если число делится на 24, то оно делится и на 2 и на 3.
