
- •Методичні рекомендації та завдання
- •Полтава 2012 рік і. Програма курсу
- •Особливості маркетингу у сфері банківських послуг.
- •3. Ринок послуг і його особливості. Банківські ринки.
- •Узгодження попиту і пропозиції у банківському маркетингу
- •Маркетинг взаємодії (відносин)
- •6. Маркетингові дослідження у банку.
- •7. Товарна політика банків.
- •8. Цінова політика у сфері банківських послуг.
- •9. Політика просування банку.
- •Конкурентоспроможність банківських послуг.
- •Іі. Методичні вказівки до розв`язання задач курсу. Методика інформаційного забезпечення
- •Вибір стратегії банку
- •Матриця бостонської групи
- •Матриця портера
- •1) Лідерство в сфері витрат —
- •2) Стратегія диференціації —
- •3) Стратегія концентрації (фокусування) —
- •Вибір місця розташування
- •Кількісні методи вибору місця розташування Зважування факторів
- •Вибір ділянки
- •Багатовузлові ділянки
- •Розташування обладнання
- •Прогнозування попиту на послуги
- •Застосування лінійного і цільового програмування у банківський сфері
- •Методика комплексної (інтегральної) оцінки об’єктів маркетингу
- •Прогнозування попиту.
- •Ііі. Завдання до контрольної роботи студентів заочної форми навчання.
- •Теоретичні питання дисципліни "маркетинг у банку"
- •Умови задачі № 1
- •Умови задачі № 2
- •Умови задачі № 3
- •Рекомендована література.
Методика комплексної (інтегральної) оцінки об’єктів маркетингу
1 Етап.
Визначити сукупність однотипних об’єктів, для яких необхідна комплексна оцінка.
2 Етап.
Вибрати локальні характеристики, спільні для всіх об’єктів,
за допомогою яких можна однозначно оцінити ці елементи, запобігаючи прямого чи непрямого дублювання цих характеристик.
3 Етап.
Знайти числове значення кожної з локальних характеристик по кожному з об’єктів, тобто сформувати матрицю натуральних значень. У цій матриці стовбці - характеристики, а строки - об’єкти.
об’єкти |
1 |
2 |
3 |
… |
… |
m |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
. |
|
|
|
Xi,j |
|
|
. |
|
|
|
|
|
|
n |
|
|
|
|
|
|
4 Етап.
У цій матриці числові значення характеристик мають різні одиниці виміру, тому математичні дії з ними не можливі. Виконаємо перетворення елементи вихідної матриці одним із наступних способів:
а)
![]() ,якщо кращим значенням характеристики
є мінімальне;
,якщо кращим значенням характеристики
є мінімальне;
б)![]() ,якщо кращим значенням характеристики
є максимальне.
,якщо кращим значенням характеристики
є максимальне.
Отримаємо нову матрицю
і |
1 |
2 |
3 |
… |
… |
m |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
n |
|
|
|
|
|
|
5 Етап.
У
ситуації, коли всі локальні характеристики
рівнозначні (рівноцінні), чого практично
не буває, то комплексна (інтегральна)
оцінка об’єктів може бути одержана як
построчна сума матриці [
].
Позиціювання об’єктів у цьому випадку
виконується по мірі зменшення даних
сум:
![]() .
.
Але завжди є підстави допустити, що характеристики будуть нерівнозначні:
а) через об’єктивні причини (внутрішня або функціональна значимість характеристик);
б) через суб’єктивні причини (зовнішня значимість);
в) через обидві вище названі причини.
6 Етап.
Оцінка внутрішньої (функціональної) значимості характеристик.
Для
цього доцільно використати метод
визначення ентропії (рівня впорядкованості).
За цим методом спочатку треба знайти
загальну суму кожного стовбця матриці
[![]() ].
Потім за формулою
].
Потім за формулою
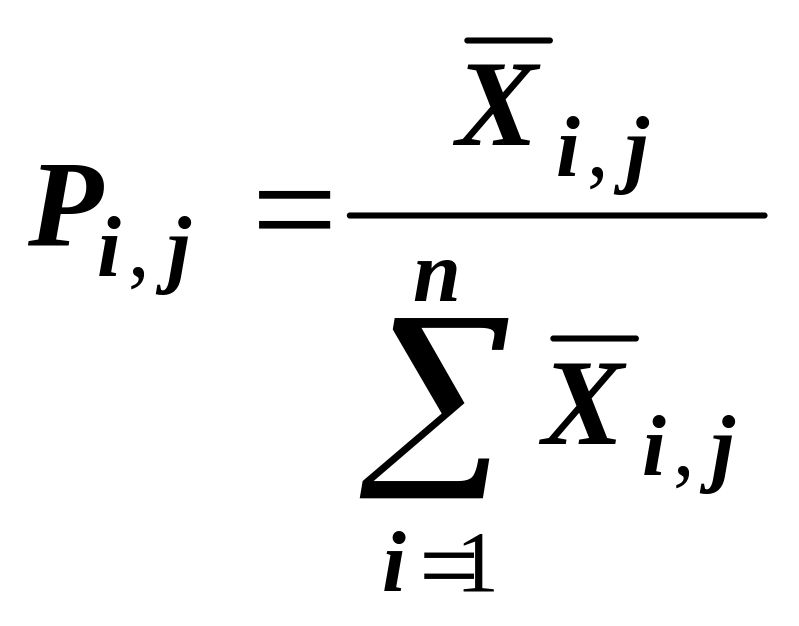 визначити
частку кожного елементу у загальній
сумі.
визначити
частку кожного елементу у загальній
сумі.
Отримаємо
матрицю [![]() ].
].
j і |
1 |
2 |
3 |
… |
… |
m |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
n |
|
|
|
|
|
|
Визначимо значення ентропії для кожного стовбця матриці [ ]:
![]() .
.
Внутрішня функціональна значимість та її приведена величина визначається за формулами
![]()
![]() .
.
7 Етап.
Визначення зовнішньої (суб’єктивної) значимості. Побудуємо матрицю попарних порівнянь.
і |
1 |
2 |
3 |
… |
… |
m |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
m |
|
|
|
|
|
|
У цій матриці і строками і стовбцями являються характеристики. Елементи матриці одержуємо, порівнюючи попарно характеристики кожну з кожною. Якщо суб’єктивна значимість даної характеристики більша, ніж та, з якою проходить порівняння, то у відповідну ячейку матриці записуємо цифру 3, якщо менша - 1, якщо вони рівнозначні - 2.
Знайшовши спочатку суму кожної строки, потім суму цих сум, визначаємо зовнішню (суб’єктивну) значимість
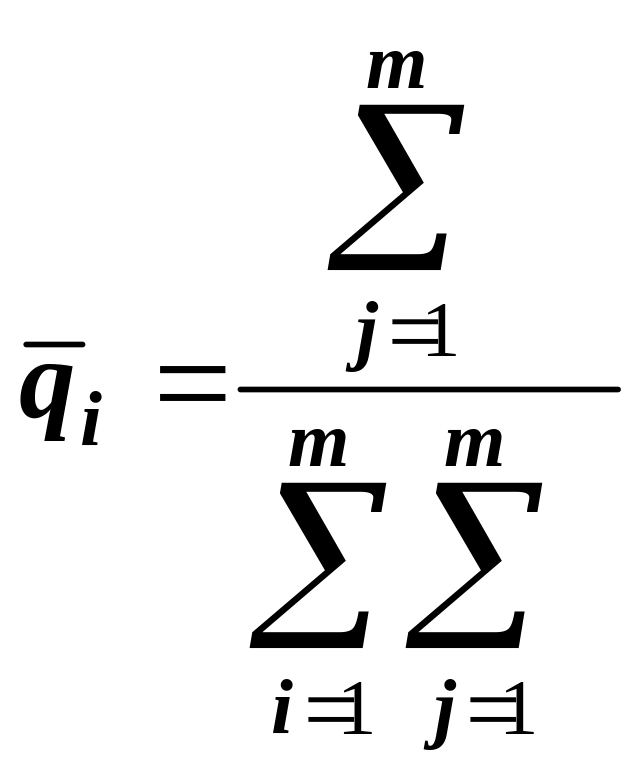 .
.
8 Етап.
При необхідності врахувати одночасно обидві значимості визначають узагальнену значимість (ki ) та її приведену величину
![]()
![]() .
.
і |
1 |
2 |
3 |
… |
… |
m |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
![]()
9. Етап.
Загальна інтегральна кількісна оцінка і-го об’єкту визначається за однією з наведених формул
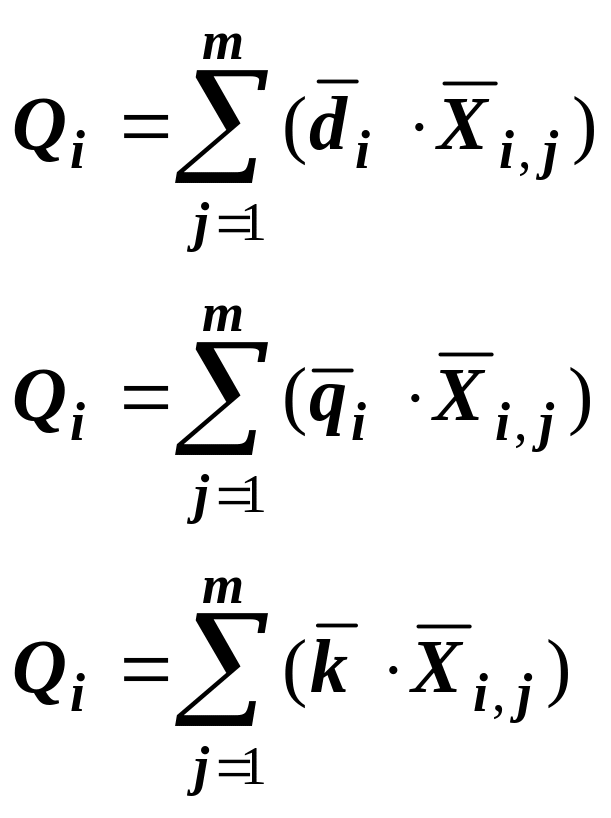

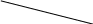 характеристики
характеристики j
j j
j j
j