Перевод чисел из одной системы счисления в другую, когда одно основание является целой степенью другого.
Как мы уже знаем, в ЭВМ наибольшее применение находит система с основаниями 2, 4, 8, 16, т.е. системы которые кратны степени 2. Поэтому целесообразно рассмотреть лишь правила перевода чисел в этих системах. Аналогичные правила будут справедливы и для других систем. Допустим, что имеется некоторое целое число N8 в 8-ой системе. Оно может быть представлено в виде:
N8 = a1*8n-1 + a2*8n-2 + a3*8n-3 + ...
+ an-2*82 + an-1*81 + an*80.
Пусть каким-либо образом мы получили запись этого числа в виде двоичного, т.е.:
N2 = b1*2k-1 + b2*2k-2 + ...
+ bk-2*22 + bk-1*21 + bk*20.
Разделим эти выражения на 23 = 8:
a1*8n-2 + a2*8n-3 + a3*8n-4 + ... + an-1*80 + an*8-1
-------
дробная часть
b1*2k-4 + b2*2k-5 + ... + bk-3*20 + bk-2*2-1 + bk-1*2-2 + bk*2-3
-------------------------
дробная часть
Так как числа были равны, то получается одинаковые частные и одинаковые остатки:
an*8-1 = bk-2*2-1 + bk-1*2-2 + bk*2-3. (6.2)
Если снова разделим целые части на 23 = 8, то опять получим равные частные и равные остатки.
При этом видим, что каждой восьмеричной цифре соответствует её двоичный эквивалент. Поэтому перевод выполняется простой заменой цифры восьмеричной системы её двоичным эквивалентом и обратно.
Пример:
62,7538 = 110010,1111010112
Аналогично для 4-ой системы:
321,22334 = 111001,101011112
Аналогично для 16-ой системы:
1D876,72 = 00011101100001110110,011100102
Из этих примеров видим, что чем выше основание системы счисления, тем компактнее запись.
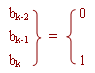
bk-2 |
bk-1 |
bk |
an |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
2 |
0 |
1 |
1 |
3 |
1 |
0 |
0 |
4 |
1 |
0 |
1 |
5 |
1 |
1 |
0 |
6 |
1 |
1 |
1 |
7 |
Если умножить последние соотношения (6.2) на 8, то:
an*8-1*8 = (bk-2*2-1 + bk-1*2-2 + bk*2-3)*23
an = bk-2*22 + bk-1*21 + bk*20
МЧС России
Санкт-Петербургский университет государственной противопожарной службы
УТВЕРЖДАЮ
Начальник кафедры ПМ и ИТ
майор внутренней службы
Т.А. Подружкина
«____» сентября 2013 г.
Методический план проведения группового занятия
по дисциплине «Информатика и информационные технологии в профессиональной
деятельности»
для обучающихся по направлению подготовки (специальности) 030901.5
«Правовое обеспечение национальной безопасности»
специализация (профиль) специалист
Тема № 1 «Введение в информационные технологии и логические основы компьютера»
Занятие № 1.3 «Расчет количества информации и работа с системами счисления»
Дата проведения занятия
Место проведения занятия: компьютерный класс
Время проведения: 2 часа.