1. Постановка і математична модель транспортної задачі

Транспортна задача відноситься до вузького класу задач лінійного програмування. Суть таких задач зводиться до того, що існує ряд пунктів, які виробляють однорідну продукцію і ряд пунктів, які споживають цю продукцію; відомі запаси кожного із постачальників і потреби кожного із споживачів, а також затрати на переміщення одиниці продукції із кожного пункта виробництва в кожний пункт споживання. Необхідно знайти оптимальний варіант закріплення постачальників за споживачами, тобто такий варіант, здійснення якого пов’язано з мінімальними витратами на переміщення продукції. Якщо позначити кількість об’єктів наявності ресурсів (постачальників) через m, об’єктів споживання ресурсів (споживачів) через n, наявність ресурсів в і-того постачальника через А_і, кількість потреб в ресурсах кожного j-того споживача через В_j, затрати на доставку одиниці ресурсів від і-того постачальника до j-того споживача через С_іj і обсяги ресурсів, які поставляються від кожного постачальника до кожного споживача через Х_іj, то структурну економіко-математичну модель задачі можна записати так:

Z _{min (max)} =

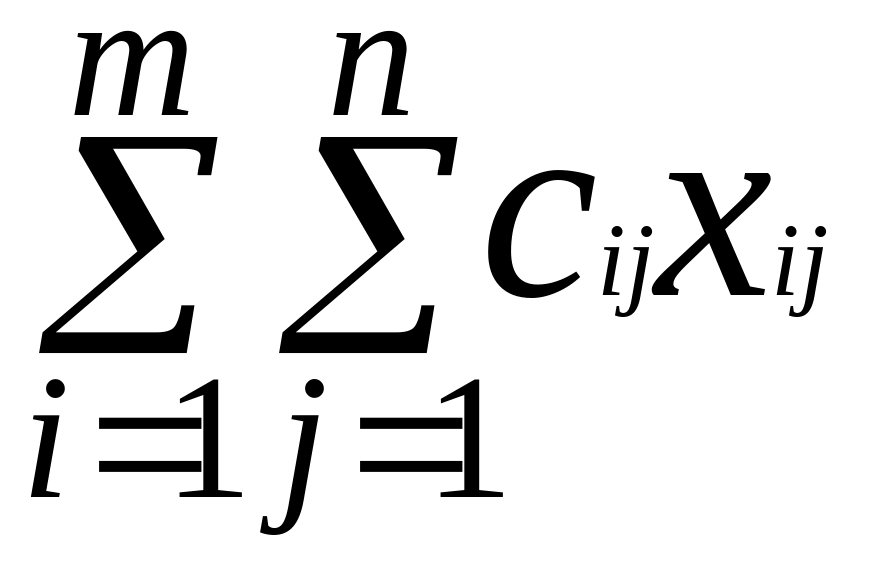
при умовах:

1. (і = 1, 2, 3,..., m)

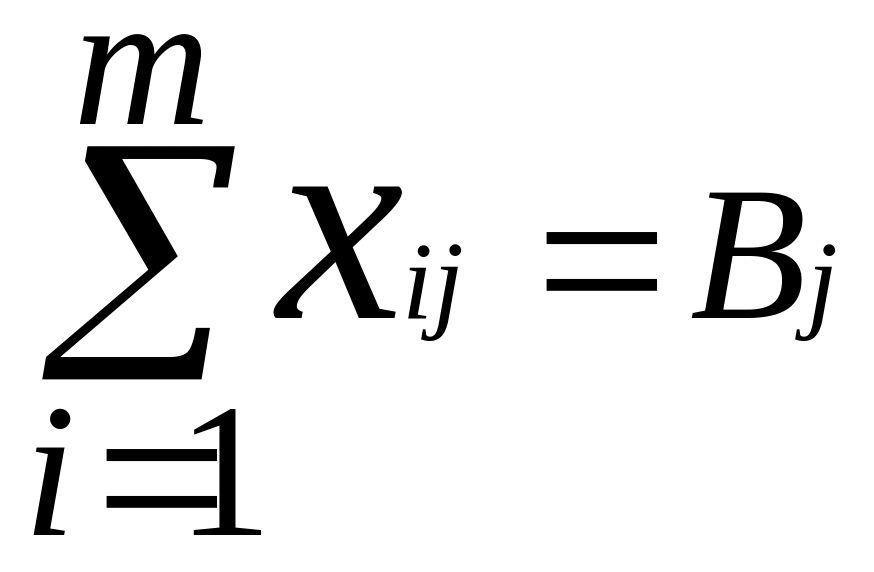2. (j = 1, 2, 3,..., n)

3.

4. x_ij >= 0

Перша умова означає, що від кожного постачальника можна вивезти лише стільки продукції, скільки у нього є, тобто сума відшукуваних обсягів перевезень від кожного постачальника повинна дорівновати наявності у них продукції.

Друга умова показує, що кожному споживачу можна завезти рівно стільки продукції, скільки йому необхідно, тобто сума відшукуваних обсягів перевезень повинна дорівнювати потребі споживачів.

Третя умова означає, що сума наявної продукції у постачальників повинна дорівнювати сумі потреб споживачів у цій продукції. Ця умова має два випадки:

а) сума наявних товарів і сума потреб у них рівні між собою. В цьому випадку модель транспортної задачі називається закритою;

б) сума наявних товарів і потреб у них не рівні між собою. В такому разі маємо справу з відкритою моделлю транспортної задачі. В практиці частіше зустрічаються задачі з відкритою моделлю. Алгоритм розв’язування транспортних задач вимагає, щоб модель була закритою. Тому в процесі розв’язування відкриту модель необхідно перетворити в закриту шляхом введення фіктивного постачальника або споживача, наявність чи потреба продукції якого дорівнювала б різниці між наявністю і потребою її у відкритій моделі. При цьому оцінки невідомих у фіктивних постачальників і споживачів рівні нулю.

Четверта умова є обов’язковою для всіх задач лінійного програмування і показує, що величина перевезень від будь-якого постачальника будь-якому споживачу не може бути від’ємною.

В розгорнутому вигляді економіко-математична модель транспортної задачі має такий вигляд:

Z _{min (max)} = c₁₁x₁₁ + c₁₂x₁₂ + … + c_ijx_ij + … + c_mnx_mn,

при умовах:

х₁₁ +х₁₂ + ... + х_1j + ... + х_1n = А₁;

х₂₁ +х₂₂ + ... + х_2j + ... + х_2n = А₂;

......................................................

х_і1 +х_і2 + ... + х_ij + ... + х_in = А_i;

……………………………………….

х_m1 +х_m2 + ... + х_mj + ... + х_mn = А_m;

х₁₁ +х₂₁ + ... + х_i1 + ... + х_m1 = B₁;

х₁₂ +х₂₂ + ... + х_i2 + ... + х_m2 = B₂;

……………………………………….

х_1j +х_2j + ... + х_ij + ... + х_mj = B_j;

………………………………………

х_1n +х_2n + ... + х_in + ... + х_mn = B_n;

A₁ +A₂ + … + A_i + … + A_m = B₁ + B₂ + … + B_j + … + B_n

x_ij >= 0 (i = 1,2,3,…, m); (j = 1,2,3, …, n)

Таблиця 12 – Модель транспортної задачі

Поста-чальники	Споживачі						Запас товарів у постачаль-ників
	1	2	...	j	...	N
1	C11 X11	C12 X12	...	C1j X1j	...	C1n X1n	A1
2	C21 X21	C22 X22	...	C2j X2j	...	C2n X2n	A2
...	...	...	...	...	...	...	...
i	Ci1 Xi1	Ci2 Xi2	...	Cij Xij	...	Cin Xin	Ai
...	...	...	...	...	...	...	...
	Cm1 Xm1	Cm2 Xm2	...	Cmj Xmj	...	Cmn Xmn	A
Потреба споживачів у товарах	B1	B2	...	Bj	...	Bn

Вся інформація транспортної задачі може мати табличний вигляд (табл.12).

Характерною особливістю транспортних задач є те, що всі невідомі змінні повинні бути виражені в одній системі виміру. В них також строго регламентована кількість змінних невідомих величин, яка дорівнює добутку m x n. Умови задачі описуються тільки рівняннями; в усіх рівняннях коефіцієнти при змінних невідомих рівні одиниці; кожна змінна зустрічається тільки в двох рівняннях системи обмежень.

Наведені вище особливості транспортних задач дали можливість розробити спеціальні методи їх розв’язування, серед яких найбільш поширені: метод потенціалів, метод диференціальних рент, розподільчий метод, метод апроксимації та інші.