Симплексний метод лінійного програмування

1. Загальна характеристика симплексного методу

Симплексний метод є універсальним методом, при допомозі якого можна знаходити оптимальне розв’язання будь-яких задач лінійного програмування. Свою назву він отримав від слова “симплекс”, яким автор методу Р.Данцінг позначив накладене на змінні х_1, х_2, …, х_n обмеження х₁+ х₂ + …+ х_n = 1. В літературі симплексний метод часто називають методом послідовного покращення плану. Ідея його в загальних рисах полягає приблизно в наступному: необхідно розв’язати будь-яку задачу, в якій треба відшукати оптимальне значення деякої лінійної форми. Вибирають початковий (більш-менш очевидний) розв’язок поставленої задачі (так званий опорний план). Після цього, пророблюють ряд послідовних кроків, які зводяться до виконання елементарних алгебраїчних перетворень, на кожному з яких одержують новий розв’язок задачі, який кращий (в крайньому разі не гірший) попереднього. Після відповідного числа кроків або одержують оптимальний розв’язок, або встановлюють, що такого розв’язку задача немає.

Особливість симплексного методу полягає в тому, що він не вимагає приведення різних величин, які вводяться в умови задачі, до єдиного вимірника, тобто виробничі ресурси і коефіцієнти затрат використовуються при розв’язуванні у звичайних, властивих для них одиницях виміру: в гектарах, людино-днях, тракторо-змінах, центнерах, гривнях і т.д. Це дає можливість вводити в умови задачі різні фактори, які в тій чи іншій мірі впливають на результати виробництва. Можливість введення в одну й ту ж задачу різних величин значно розширює коло задач, які розв’язуються симплекс-методом. Так, у сфері економіки і планування сільського господарства цим методом розв’язують дуже багато задач, зокрема таких як визначення оптимальної виробничої структури і спеціалізації сільськогосподарських підприємств різних форм господарювання, розрахунок оптимальних раціонів годівлі сільськогосподарських тварин, визначення оптимального плану виробництва і використання кормів, визначення оптимального плану використання заготовлених кормів, визначення оптимальної структури стада різних видів сільськогосподарських тварин і інші.

2. Математичне формулювання задачі

При формулюванні задачі лінійного програмування, яка розв’язується симплексним методом, в першу чергу необхідно визначити можливості виробництва. Вони виражаються відношеннями, які накладаються обмеженнями на обсяги і поєднання різних видів виробничої діяльності. Відношення визначають сумарну потребу різного виду ресурсів і виражаються в виді нерівностей. Такі нерівності, як правило, не вимагають повного використання наявних в господарстві ресурсів. Вони вказують на те, що при складанні будь-якого плану буде використано ресурсів не більше, ніж їх є в наявності.

Можливості виробництва, які є в розпорядженні господарства, можна описати системою нерівностей типу:

a_i1x₁ + a_i2x₂ + … + a_inx_n <= b_i ( i = 1, 2, …, m )

або, використовуючи знак суми S, в більш компактній формі:

( i = 1, 2, …, m )

Є задачі лінійного програмування, умови яких не можна виразити нерівностями типу “<=”. Наприклад, коли необхідно розрахувати кормовий раціон, який би містив не менше відповідної кількості поживних речовин, або сформулювати обмеження , які би відображали вимоги по гарантованому обсягу виробництва відповідної продукції, то математичне вираження цих умов може бути представлено системою нерівностей типу:

a_i1x₁ + a_i2x2 + … + a_inx_n >= b_i ( i = 1, 2, …, m )

або більш компактно:

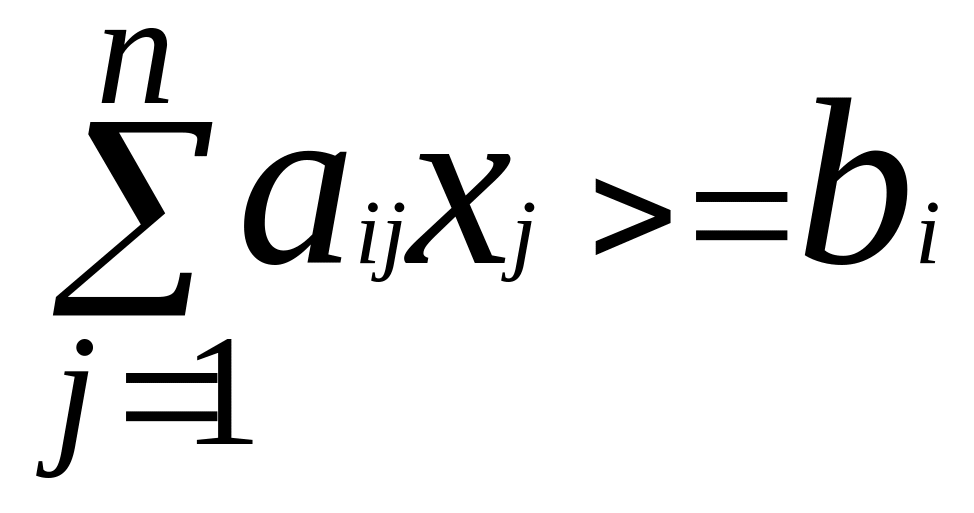( i = 1, 2, …, m )

В деяких випадках для математичного вираження задачі лінійного програмування користуються системою рівнянь:

a_i1x₁ + a_i2x2 + … + a_inx_n = b_i ( i = 1, 2, …, m )

або в загальній формі:

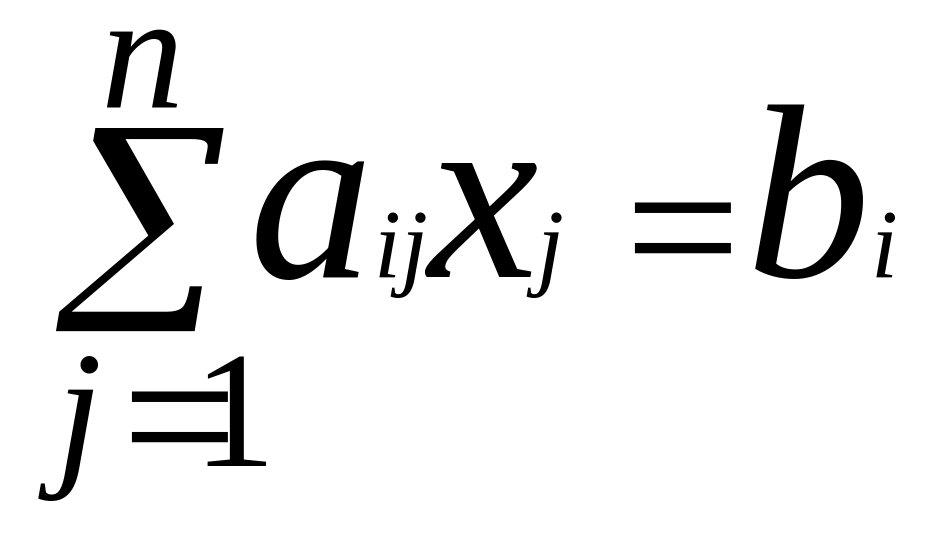( i = 1, 2, …, m )

Рівняннями цього типу виражаються так звані тверді обмеження, поскільки вони вимагають повного використання наявних в господарстві ресурсів.

Поскільки відшукувані змінні величини x₁, x₂, …, x_n, які означають обсяги виробничої діяльності або кількість виробленої продукції, повинні бути більшими чи рівними нулю, тобто не повинні бути від’ємними, тому для забезпечення цієї вимоги, застосовують нерівності типу:

x₁ >=0, x₂ >= 0, …, x_n >= 0,

або в загальній формі:

x_j >= 0 ( j = 1, 2, …, n ).

Після визначення можливостей виробництва формулюється мета задачі у вигляді лінійної функції, чи функціоналу, яка виражається наступним рівнянням:

Z (_{max, min}) = C₁X₁ + C₂X₂ + … + C_nX_n,

або

Z (_{max, min}) =

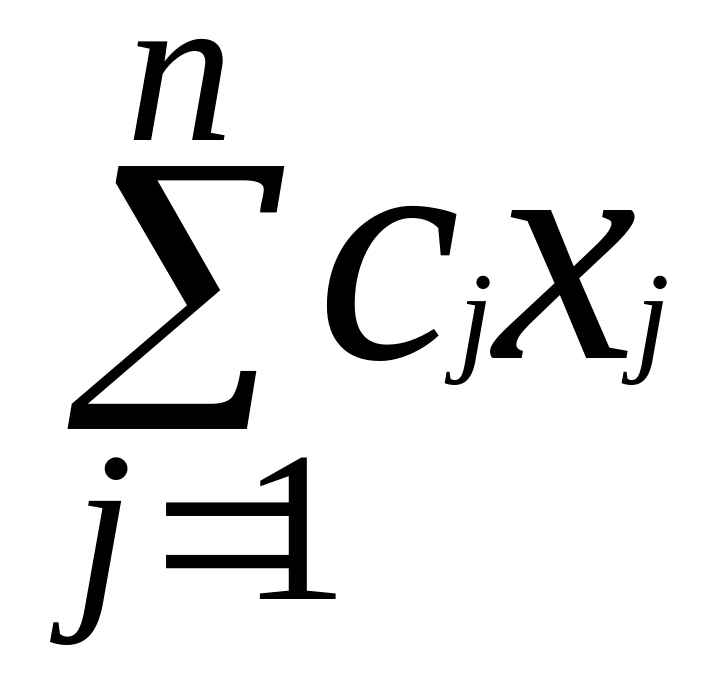
При розв’язуванні задачі лінійного програмування симплексним методом із використанням симплексних таблиць умови, які виражені нерівностями, перетворюють в рівняння, тобто задача зводиться до канонічної форми.