11

Основные положения механики деформируемых сред (Курс «Теория процессов трубного производства.

Раздел 1 Напряжения в сплошной среде.

1.1. Силы и напряжения

Если к телу приложены внешние силы и создано препятствие свободному движению его, то тело находится в напряженном состоянии. Внешние силы, возникающие от действия машин орудий на тело, называют активными силами (рис.1).

Рис.1. Вектор напряжения на произвольной площадке в сплошной среде

Обозначим внешние силы Р_n действующие на тело площадью F, главный вектор всех сил, действующих на сплошную среду через . Активные силы вызывают сближение или удаление частиц внутри сплошной среды. Внутри сплошной среды рассмотрим некоторый бесконечно малый объем, в виде куба с ребрами dx,dy,dz (рис.2). На каждую грань куба действуют напряжения (где ∆ F -площадь грани куба, ∆ - усилие, действующее на грань куба), которые можно разложить по базису в принятой системе координат ох₁, ох₂; ох₃ на 3 составляющие. вектора ( ; ; ):

(1)

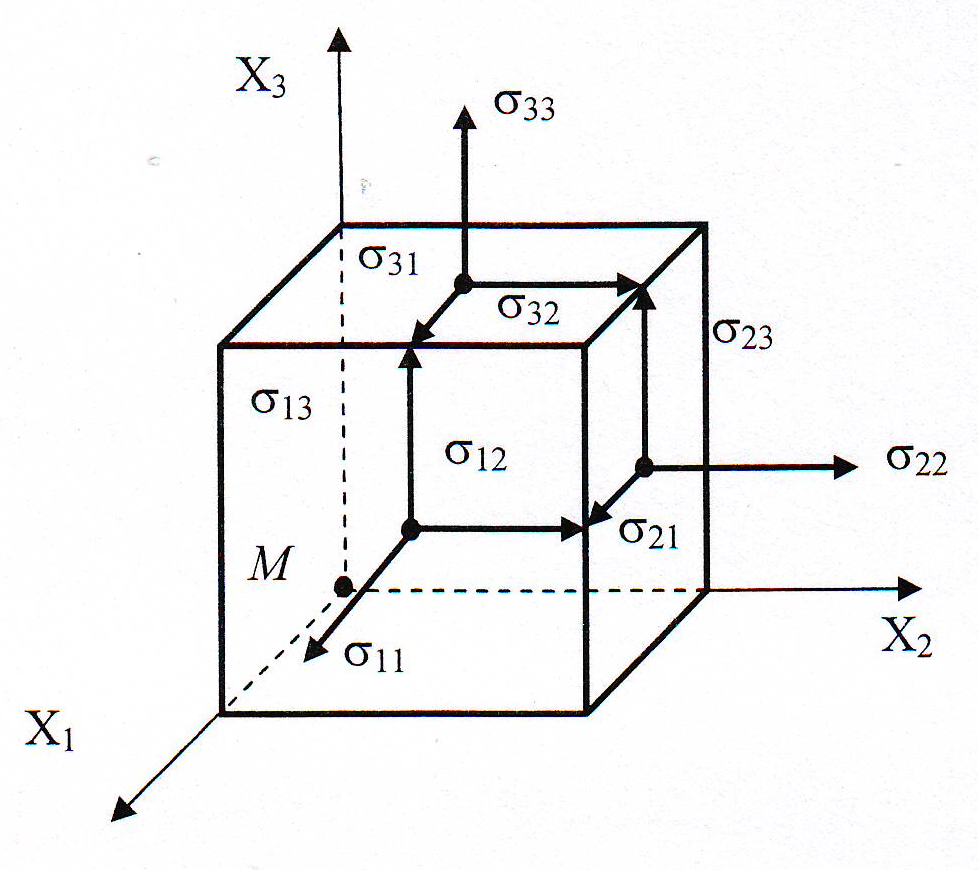
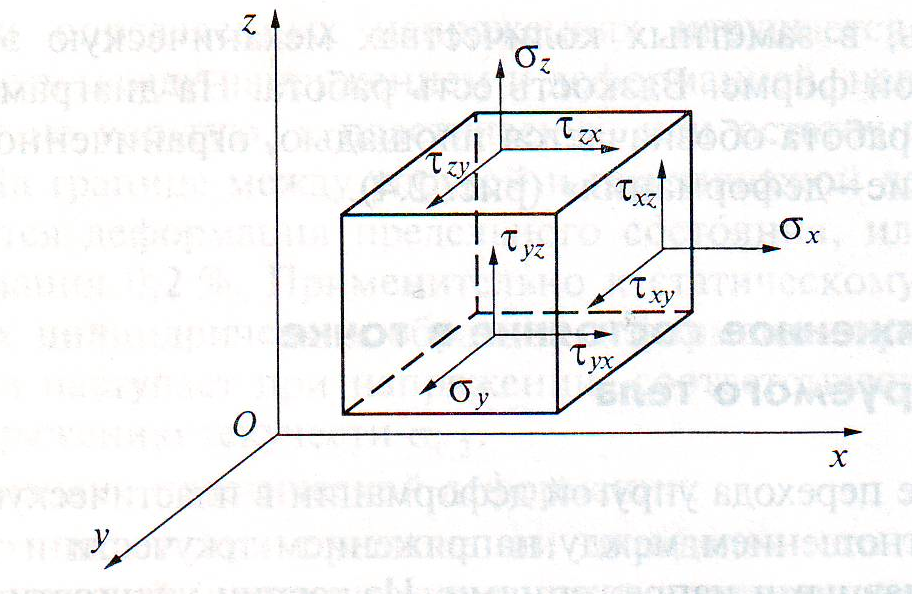
Коэффициенты разложения σ_ij образуют тензор напряжения; первый индекс показывает, на какой площадке действует напряжение, а второй – в каком направлении. В соответствии с этим напряжение σ_ij, которое при i = j будет σ_ii и называется нормальным и при i ≠ j σ_jj – касательным напряжениями. В уравнениях системы (1) нормальные напряжения обозначены так: σ₁₁; σ₂₂; σ₃₃; касательные напряжения обозначены так:

σ₁₂; σ₁₃; σ₂₁; σ₂₃; σ₃₁; σ₃₂; общепринятым также является и следующая запись напряжений: нормальных σ₁₁ = σ_х; σ₂₂ = σ_y; σ₃₃ = σ_z и касательных - σ₁₂ = τ_х,y; σ₁₃ = τ_х,z

σ₂₁= τ_y,х; σ₂₃ = τ_y,z; σ₃₁ = τ_z,х; σ₃₂ = τ_z,y (рис.2)

Рис.2. Нормальные и касательные по трем площадкам элементарного объема – куба.

Всех напряжений на координатных площадках девять: три нормальных и шесть касательных. Из положения о парности ка­сательных напряжений известно, что парные касательные напря­жения отличающиеся порядком индексов) равны, т. е.

τ_х,y = τ_y,х; τ_y,z = τ_zy ; τ_zx = τ_х,z

Таким образом, напряженное состояние в точке определяется 6 напряжениями: 3 нормальными и 3 касательными (рис.2).

2. Главные напряжения.

Главные нормальные напряжения. Если грани выделенного элементарного куба совпадают с осями выбранной системы координат, то такие оси называются главными осями их принято обозначать индексами 1, 2, 3 вместо х, y , z, а напряжения, действующие на гранях куба, называются главными напряжениями и в этом случае на гранях куба будут действовать только нормальные напряжения σ₁; σ₂; σ₃, а касательные напря­жения будут равны 0 (нулю)

-

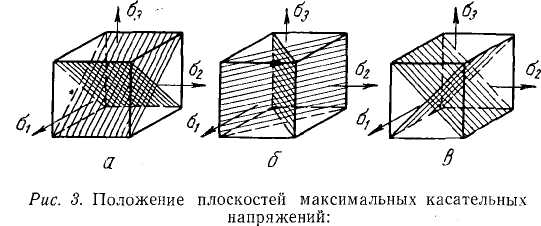
Главные касательные напряжения. Внутри выделенного элементарного куба также действуют напряжения: нормальные и касательные. На главных меридиональных площадках действуют максимальные касательные напряжения:

а - ; б - в -

и нормальные напряжения: ; ;

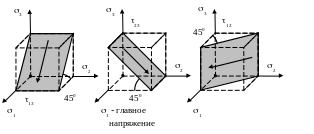
Рис.4. Максимальные касательные напряжения, действующие на главных меридиональных площадках.

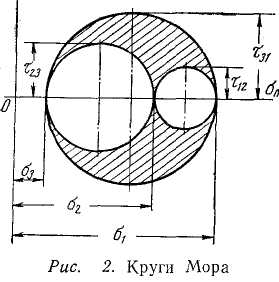
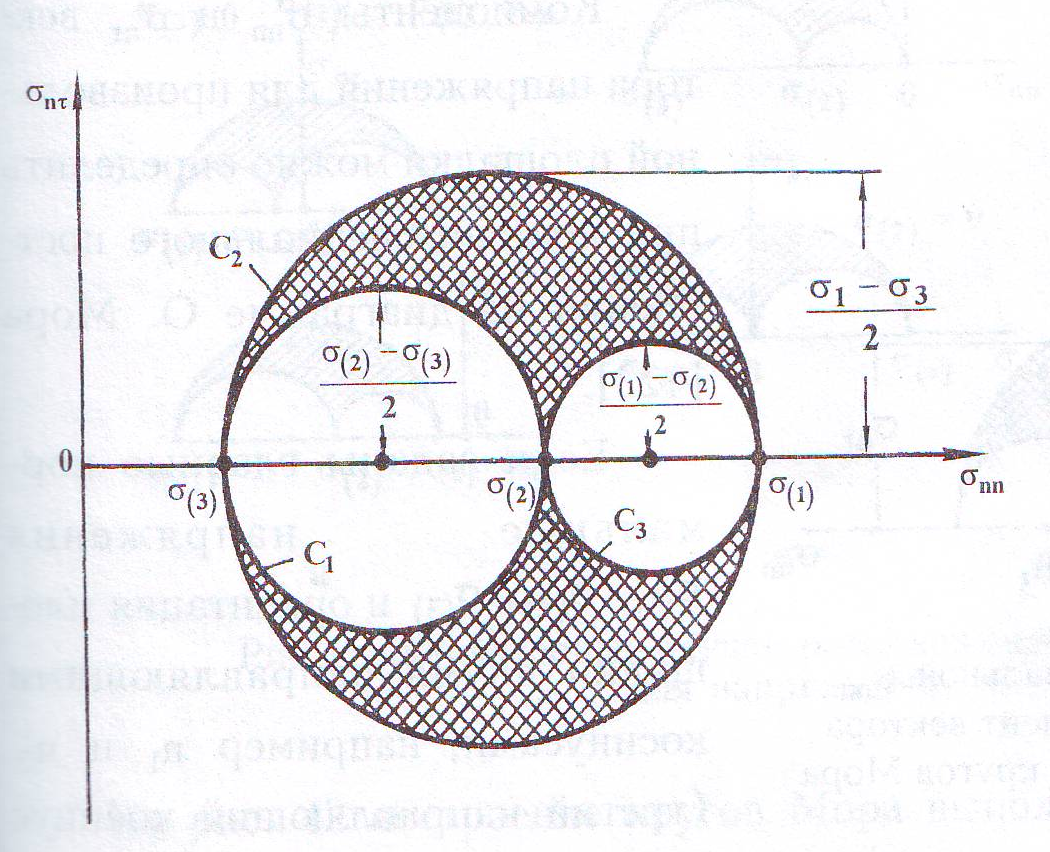
Графическое представление напряженного состояния в точке дает диаграмма Мора известная в литературе как круги Мора (рис.5).

Рисунок 5. Круги Мора для напряжений.

На рис.6 показаны круги Мора для трех основных типов напряженного состояния.

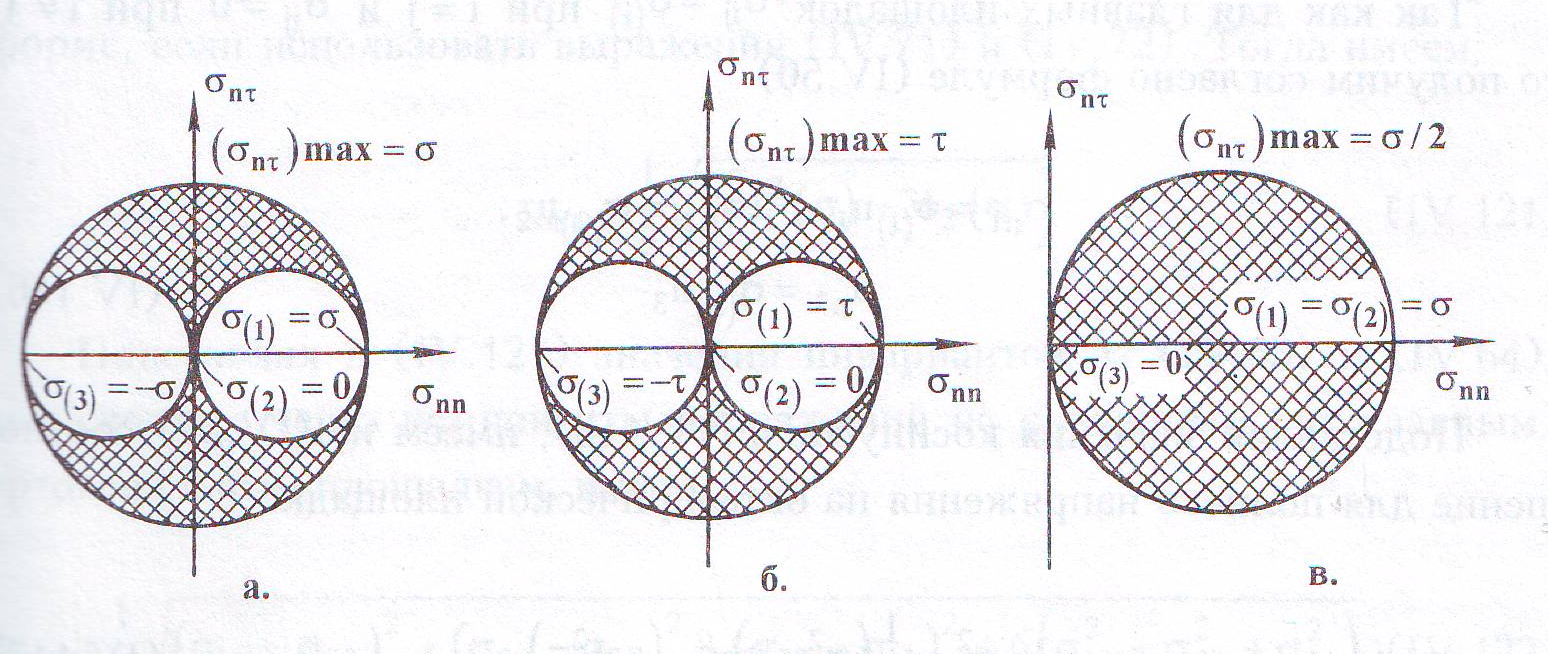
Рисунок 6. Круги Мора для трех основных типов напряженного состояния: а – σ₁ = σ; σ₃ = σ; б – σ₁ = τ; σ₂ =0; σ₃ = - τ; в - σ₁ = σ₂ = σ; σ₃ = 0

Следовательно, соотношения между σ_n и τ определяются коор­динатами точек, лежащих внутри заштрихованной площади круга