§2. Алгоритм решения задач теплопроводности и диффузии методом интегральных преобразований

1. Постановка задачи

   1. Выписать дифференциальное уравнение.

   2. Выписать начальное условие.

   3. Выписать граничные условия.

   4. Нарисовать график начального условия.

2. Аналитическое решение задачи

   1. Выбор ядра: воспользоваться таблицами Карташова для выбора – ядра интегрального преобразования.

   2. Выписать интегральное преобразование

.

3. Преобразовать задачу (3.1) к задаче Коши вида

(3.4)

Замечание 1. Как известно из раздела "Обыкновенные дифференциальные уравнения", решение задачи Коши

имеет вид

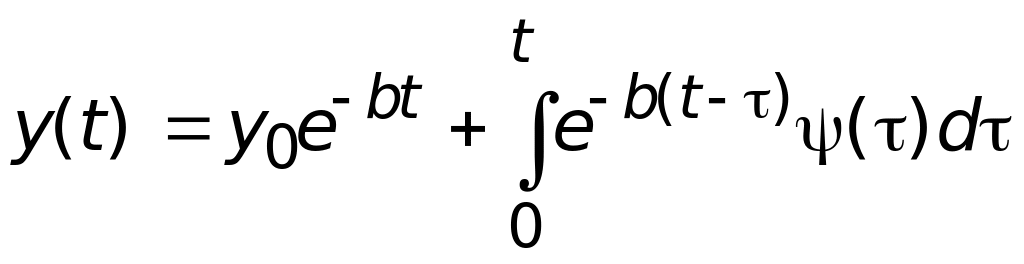. (3.5)

Замечание 2. При переходе от задачи (3.1) к задаче (3.4) надо различать следующие этапы:

а) поменять левую часть уравнения на ,

б) выписать из таблиц Карташова изображение второй производной и получить свою функцию и константу b;

в) выполнить интегральное преобразование начального условия и получить y₀ .

4. Выписать решение полученной задачи.

5. С помощью формулы обращения найти функцию T(x,t)

. (3.6)

В случае задачи 2.2 в формуле обращения появляется дополнительное слагаемое и формула обращения имеет вид

. (3.7)

3. С помощью таблиц Карташова (прил.2) улучшить полученное решение, т.е. прибавить и вычесть указанные в таблице функции .

4. Анализ полученного решения

4.1.Выписать первые два ненулевых члена ряда в полученном решении.

4.2. Нарисовать графики функции T(x,t) для нескольких фиксированных значений времени t.

§3. Решение 1-й краевой задачи методом интегральных преобразований

1. Постановка задачи. Рассмотрим первую краевую задачу без источника для одномерного случая

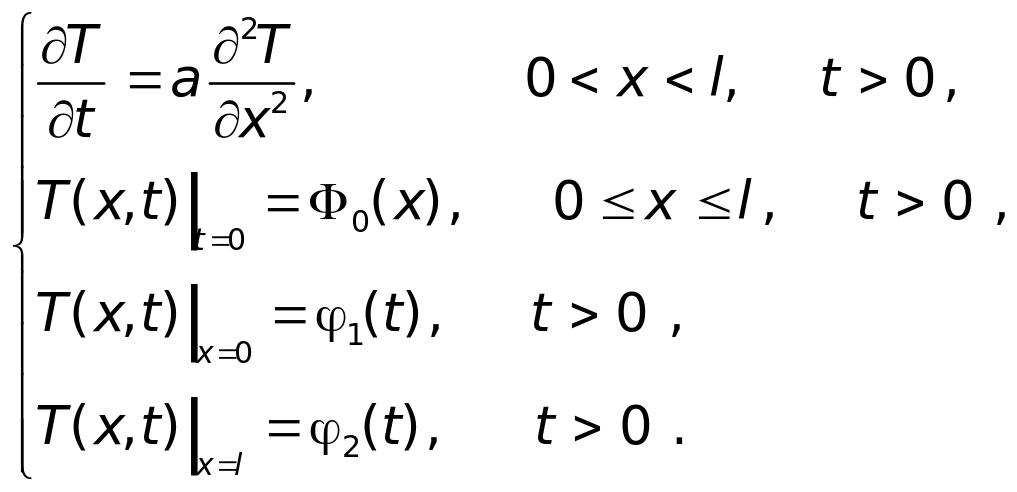(3.8)

Наша цель найти такую функцию T(x,t), чтобы она удовлетворяла условиям (3.8).

2. Аналитическое решение задачи. Воспользуемся таблицами Карташова и найдем ядро интегрального преобразования для задачи (3.8) (граничная задача 1.1), это

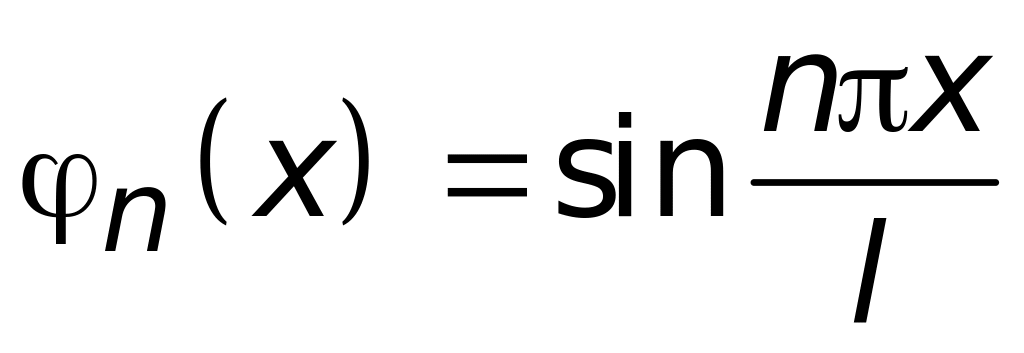
Выпишем интегральное преобразование функции T(x,t)

(3.9)

с формулой обращения

. (3.10)

Преобразуем задачу (3.8) так, чтобы перейти от функции

T(x,t) к функции . Для этого учтем, что

и, далее, выпишем из таблиц Карташова изображение второй производной

.

Затем выполним интегральное преобразование начального условия, тогда получим

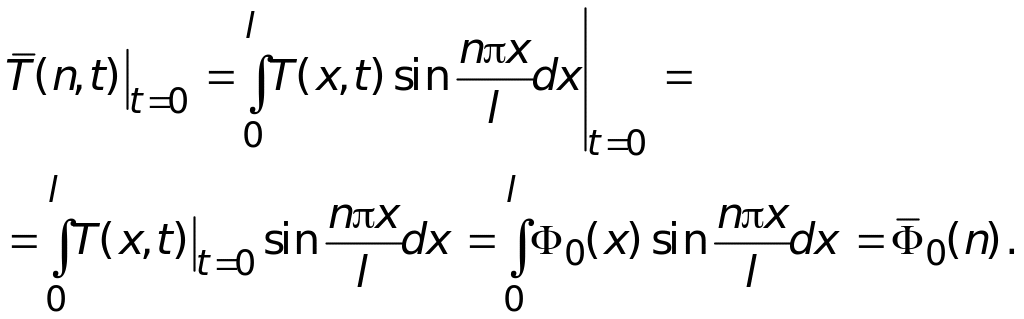
Таким образом, вместо задачи (3.8) имеем задачу Коши

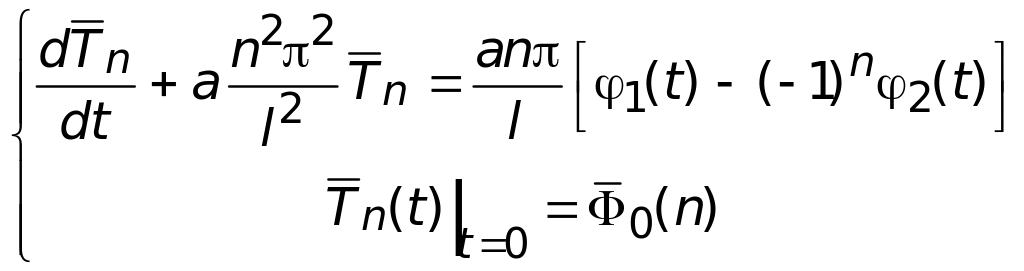(3.11)

Замечание. Если сравнить с задачей (3.4), то

.

Таким образом, согласно (3.5), находим решение задачи (3.11)

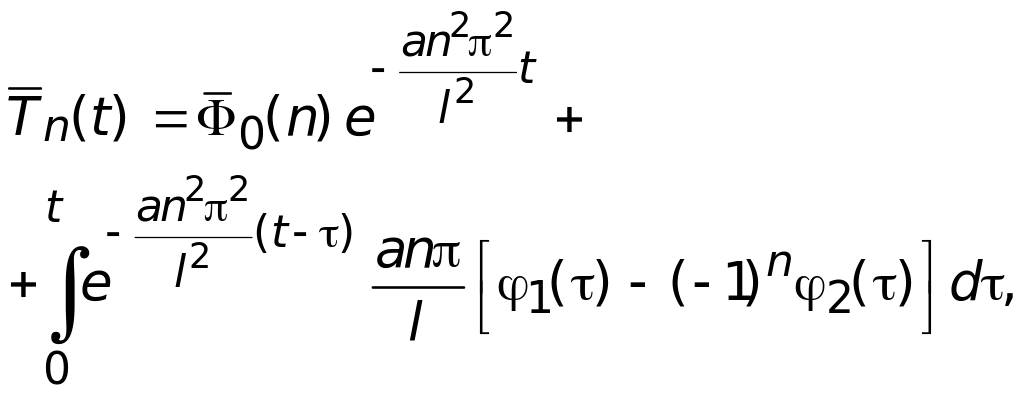(3.12)

используя формулу обращения (3.10), получим

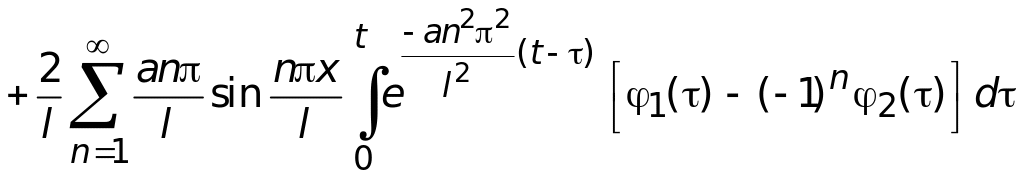(3.13)

С помощью таблиц Карташова (прил.2) улучшим полученное решение, т.е. прибавим и вычтем указанные в таблице функции, тогда имеем

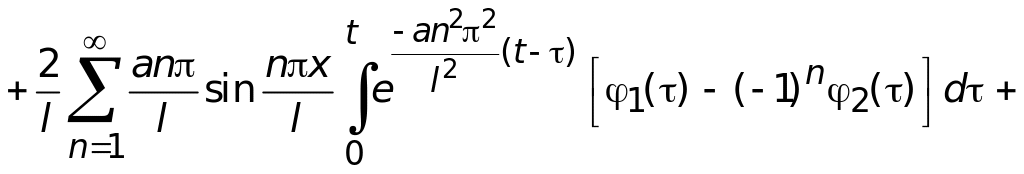
(3.14)

Упражнение. Выписать решение этой задачи для , — постоянных краевых условий.

Часть 4. Операционное исчисление §1. Преобразование Лапласа

Операционное исчисление — раздел математики, основанный на интегральном преобразовании специального вида, называемом преобразованием Лапласа.

Преобразование Лапласа — интегральное преобразование с ядром K(p,t) =  , где p = w + is — комплексная переменная. Оно определено на интервале для функций f(t), обладающих следующими свойствами:

1) f(t) — кусочно-непрерывная функция,

2) f(t) = 0 при t < 0,

3) │f(t)│≤ Me^mt , (при t → функция f(t) может возрастать, но не слишком быстро, не быстрее e^mt).

Это преобразование имеет вид

,

— называют изображением функции f(t), а функцию f(t) называют оригиналом изображения и обозначают

.

(Обратите внимание, что стрелка направлена от оригинала к изображению).

Чтобы найти область сходимости преобразования Лапласа, оценим интеграл

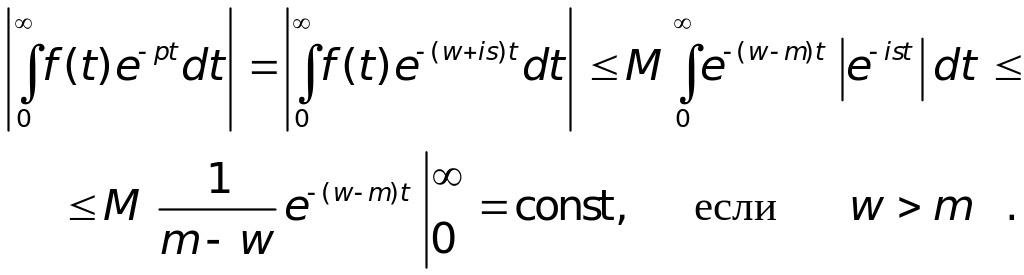
Здесь мы учли, что . Область сходимости интеграла w = Rep > m.

Необходимое условие сходимости преобразования Лапласа.

Если функция — изображение некоторой функции, то

.

Замечание. Например, если = , то сразу можно сказать, что эта функция не является изображением какой либо функции f(t). Однако данное условие не является достаточным, т.к. можно привести пример функции, для которой это условие выполнено, но нет оригинала. Например, для функции , но нет оригинала (в пространстве элементарных функций).

Для изображения и оригинала справедливы следующие предельные соотношения:

— теорема о начальном значении, — теорема о конечном значении

Пример 1. Найти изображение функции f(t) = 1. Для того чтобы найти изображение этой функции, вычислим интеграл

Таким образом, 1

Замечание 1. Здесь и везде далее, когда мы пишем f(t) = 1, то подразумеваем, что

.

Пример 2. Найти изображение функции f(t) = :

Таким образом

Пример 3. Найти изображение функции f(t) = t

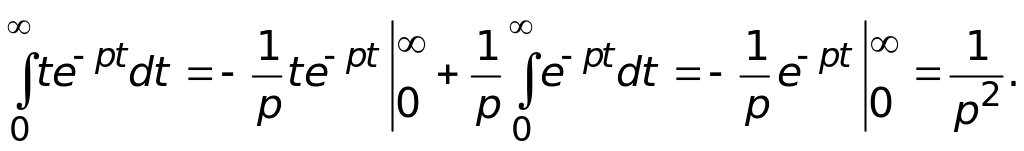
Таким образом, t

Замечание 2. Нетрудно проверить, что

Пример 4. Найти изображение функции

Выпишем преобразование Лапласа этой функции и дважды проведем интегрирование по частям:

Решая уравнение , получим, что

.

Упражнение. Показать, что .