§6. Примеры разложения в тригонометрический ряд Фурье функции f(X)

Пусть функция f(x) = x задана на отрезке [0,π]. Приведем три разложения этой функции в ряд Фурье.

1) Продолжим функцию f(x) на отрезок [–π,0] нечетным образом, тогда f(x) = x на [–π,π]. Найдем коэффициенты ряда Фурье. Согласно (1.19)

.

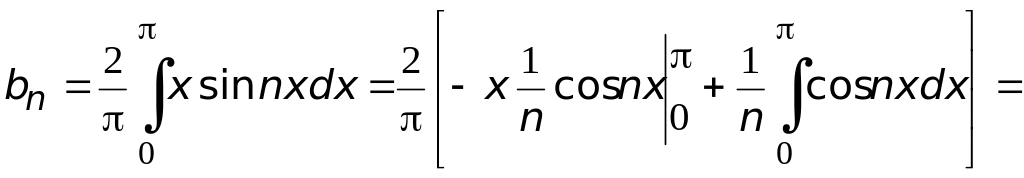
Замечание. Полезно напомнить, что

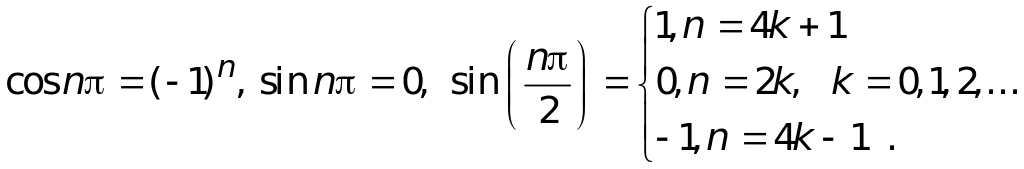
Таким образом, ряд Фурье для функции f(x) = x на отрезке [0,π] имеет вид

.

Его сумма совпадает с функцией f(x) на интервале [0,π), а в точке x = π имеем S(π) = 0 ≠ f(π) = π (см. рис.1).

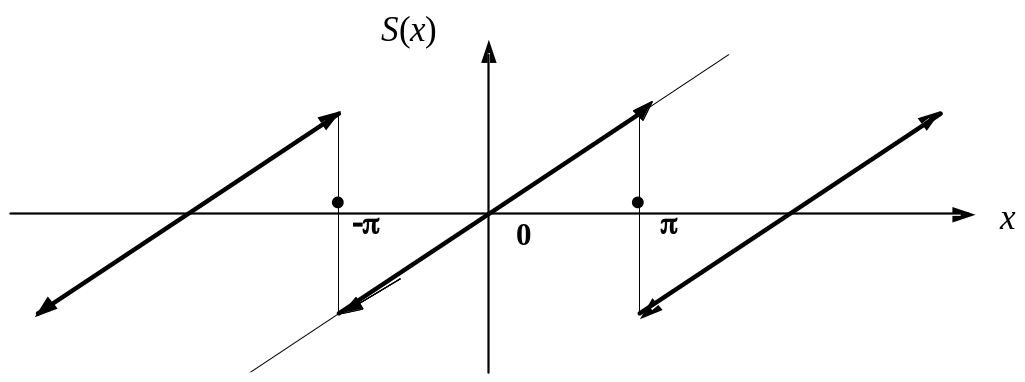Рис. 1.

2) Продолжим функцию f(x) на отрезок [–π,0] четным образом:

.

Найдем коэффициенты ряда Фурье. Из (5.3) и (5.4) имеем

,

Таким образом, ряд Фурье для функции f(x) имеет вид (см.р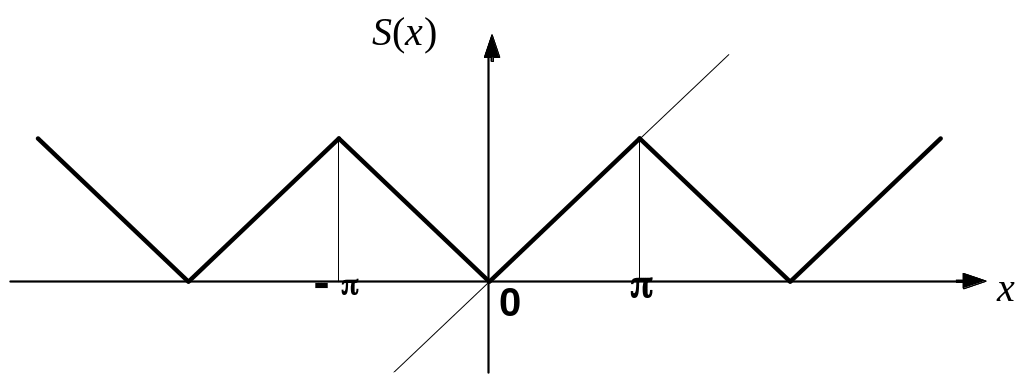ис.2)

Рис. 2.

3) Продолжим функцию f(x) на отрезок[–π,0] следующим образом:

.

Найдем коэффициенты тригонометрического ряда Фурье

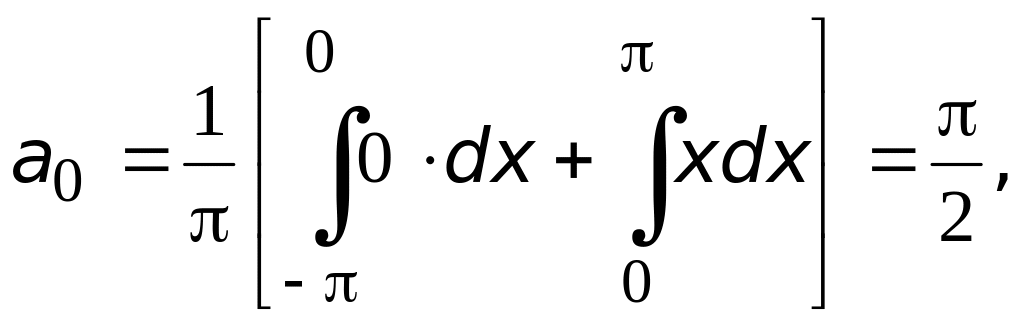
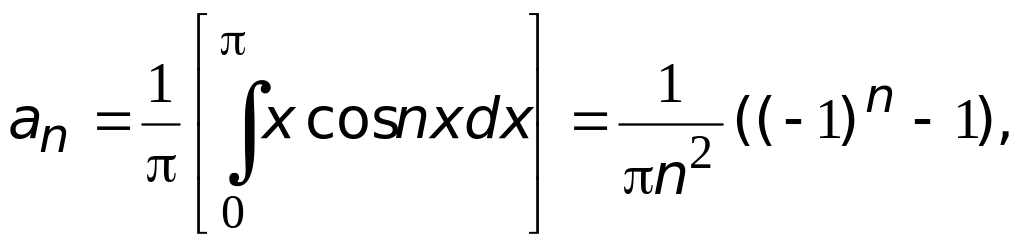
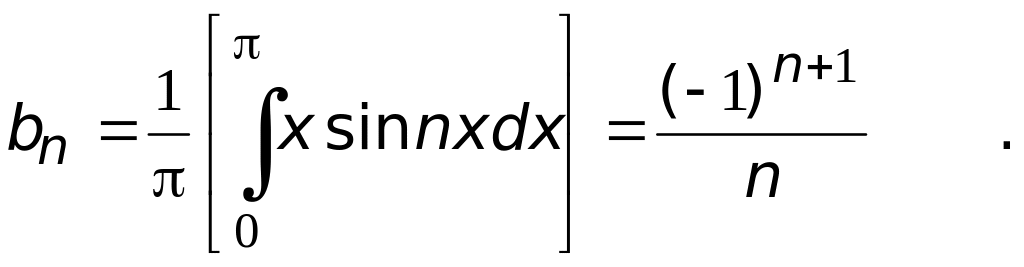
Ряд Фурье в этом случае будет иметь вид (см. р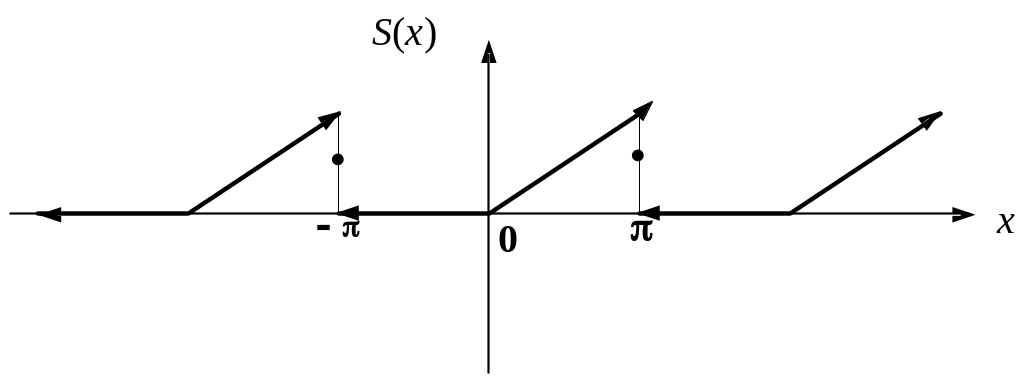ис.3)

.

Рис. 3.

Сумма этого ряда Фурье S(x) будет совпадать с функцией f(x) в точках интервала [0,π), а в точке x = π S(π)  f(π), (S(π) = π/2, f(π) = π).

Часть 2. Математическое моделирование физических и химических процессов §1. Основные положения теории тепло- массопереноса

Пусть в твердом теле различные его части нагреты до различных температур. В этом случае в теле возникнут направленные потоки теплоты от мест с большей температурой к местам с меньшей, т.е. возникнет перенос теплоты. Это и есть процесс теплопроводности.

Пусть мы имеем некоторый объем, в котором находится вещество, причем в разных частях этого объема находится разное количество вещества. Тогда в этой среде возникнут направленные потоки вещества от мест с большей концентрацией к местам с меньшей концентрацией, т.е. возникнет процесс диффузии, состоящий в выравнивании концентрации вещества по всему объему.

Справка из математического анализа

• Скалярное поле. Если в каждой точке пространственной области  задана скалярная функция T(x,y,z), то, говорят, что в области  задано скалярное поле.

• Производная по направлению. Пусть в пространственной области  задана функция T = T(x,y,z) и в точке (x₀,y₀,z₀) указано некоторое направлени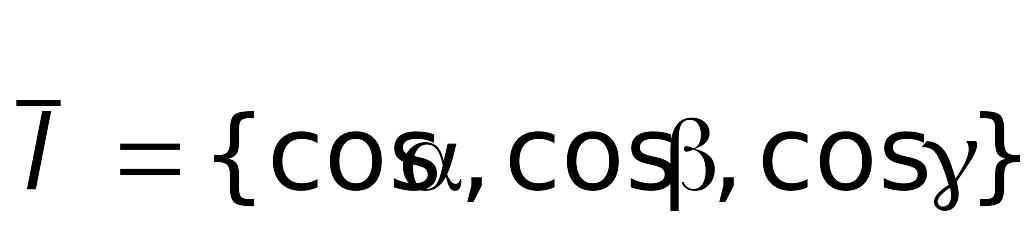е , где 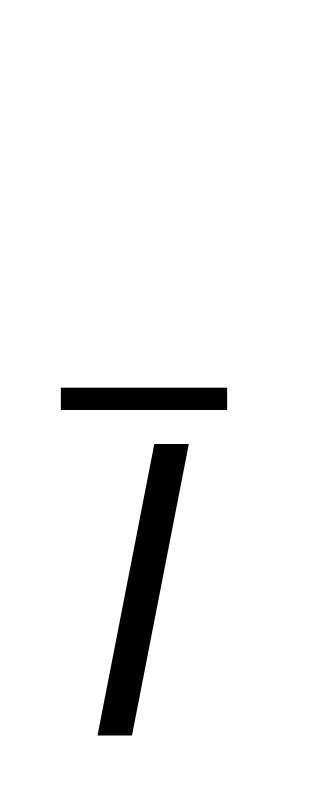– единичный вектор (орт), 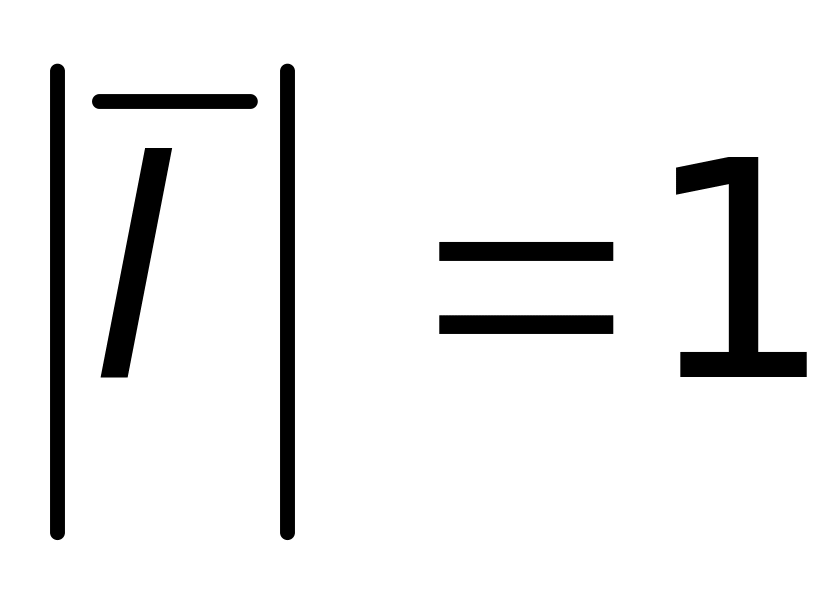, а – направляющие косинусы. Тогда производной функции T(x,y,z) по направлению 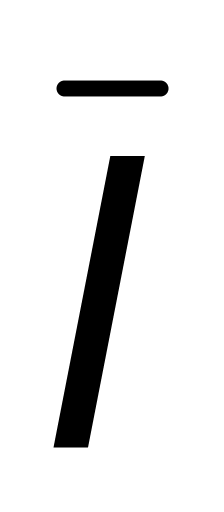в точке (x₀,y₀,z₀) называется величина

.

• Градиент функции. Среди всевозможных направлений можно выделить одно, по которому скорость изменения функции T является максимальной; это направление задается вектором, который называется градиентом функции T(x,y,z) (или градиентом скалярного поля T(x,y,z))

.

Производная по направлению и градиент функции T(x,y,z) связаны формулой (производная по направлению равна скалярному произведению векторов gradT и ).

Поверхностью уровня скалярного поля T(x,y,z) называется такое множество точек (x,y,z)Î, что значение функции T(x,y,z) постоянно на всем этом множестве. Таким образом, V ‑ поверхность уровня (V), если для любой точки (x,y,z)ÎVзначение функции T(x,y,z) = const. Через каждую точку (x,y,z) области  проходит одна единственная поверхность уровня (поверхности уровня не пересекаются). Градиент функции T(x,y,z) в данной точке перпендикулярен поверхности уровня, проходящей через данную точку. Скалярное произведение – нормали к поверхности уровня, на градиент функции T(x,y,z) равен производной функции T(x,y,z) по направлению нормали , т.е.

.