Министерство образования и науки Российской Федерации

Московский государственный университет тонкой химической технологии им. М.В.Ломоносова

Кафедра высшей и прикладной математики

И.А.Джемесюк, Э.М.Карташов, А.Г.Рубин

Краткий курс математического моделирования физико-химических процессов

Учебно-методическое пособие

Москва

Издательство МИТХТ

2012

УДК 51

ББК 22.1

Рецензент – доктор физико-матеметических наук профессор Шевелев В.В.

Учебно-методическое пособие. М.:ИПЦ МИТХТ, 52 с.

Утверждено библиотечно-издательской комиссией

в качестве учебно-методического пособия

для студентов 2–4-го курсов дневного отделения

всех специальностей МИТХТ им. М.В.Ломоносова

по дисциплине "Прикладная математика", поз. /2012.

 МИТХТ им. М.В.Ломоносова, 2012.

Ч асть 1. Ряды Фурье §1. Ортогональные системы функций

Определение 1. Нормой функции (x) на отрезке [a,b] называется число

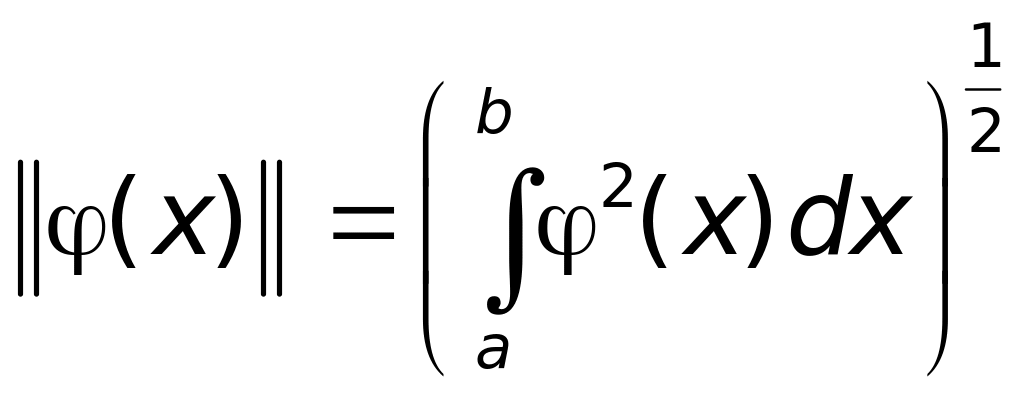. (1.1)

Замечание. В практических расчетах мы будем иметь дело с квадратом нормы.

Определение 2. Система функций {_n(x)}, n = 1,2,3…, заданных на отрезке [a,b], называется ортогональной на этом отрезке, если

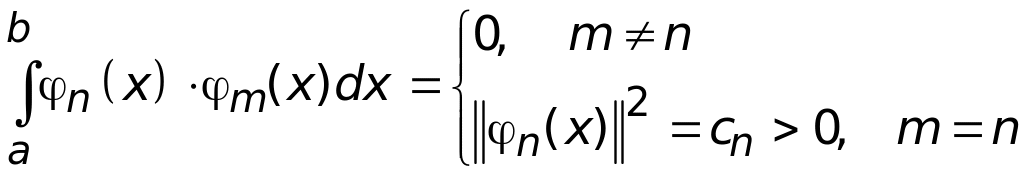. (1.2)

Пример 1. Показать, что система функций

n = 1,2,3,… (1.3)

является ортогональной на отрезке [–l,l].

Замечание. Система функций (1.3) называется классической тригонометрической системой.

Решение. Чтобы показать, что эти функции образуют ортогональную систему, надо проверить верность следующих равенств

1) ;

2) ;

3) ;

4) ;

5)

и найти нормы этих функций, т.е. вычислить интегралы

. (1.4)

Замечание. Нам потребуются следующие тригонометрические формулы:

;

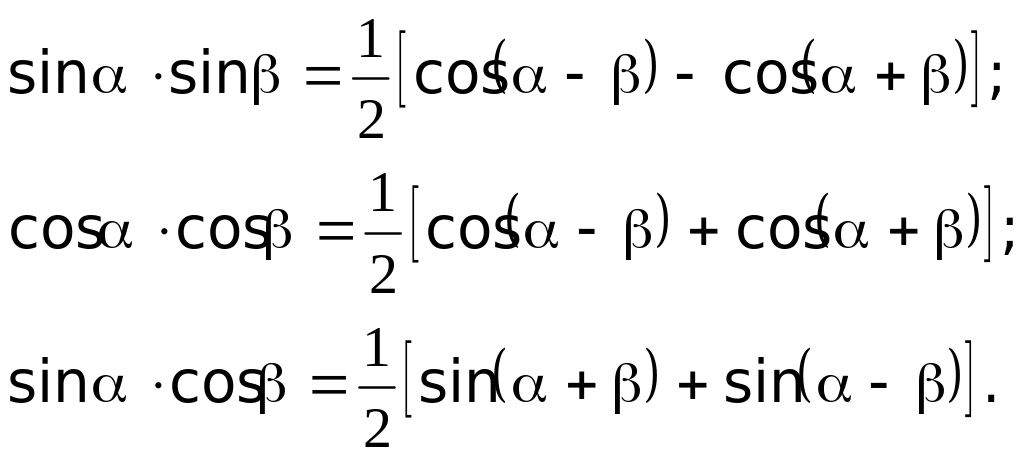
Докажем соотношения 1) и 3).

;

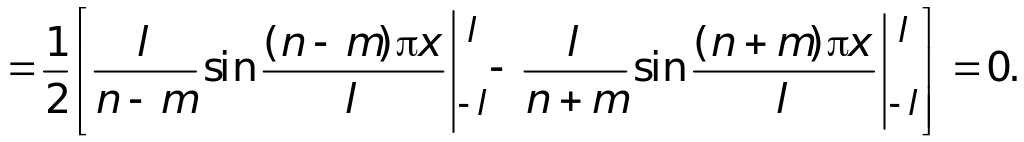
Упражнение 1. Самостоятельно доказать равенства 2), 4) и 5).

Вычислим квадраты нормы каждой из функций (1.3)

,

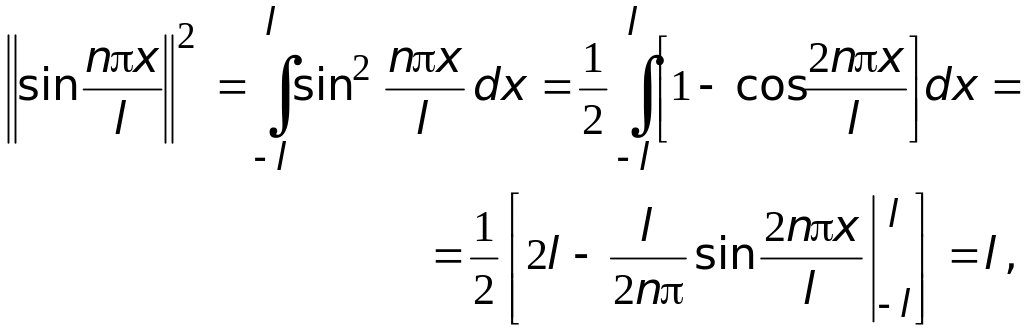
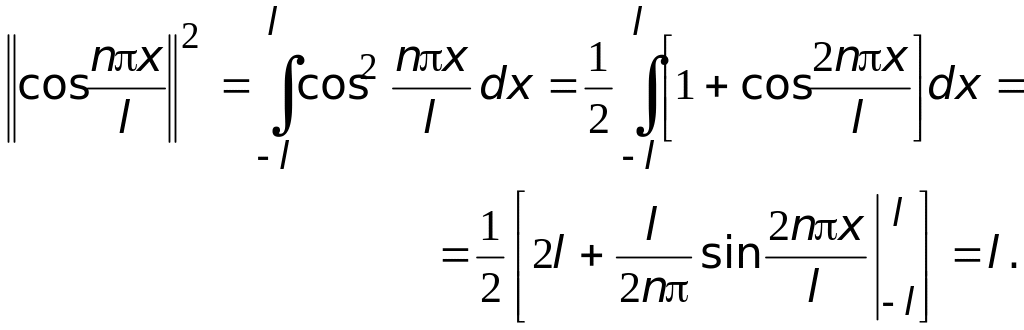
Замечание. Очевидно, что любая часть (подсистема) системы ортогональных функций является ортогональной. Например, системы функций и тоже являются ортогональными на отрезке [–l,l].

Упражнение 2. Показать, что система функций {1, sinx,cosx,…, sinnx, cosnx,…} является ортогональной на отрезке [–π,π] и найти норму каждой из этих функций.

Упражнение 3. Показать, что система функций , n = 1,2,3,… является ортогональной на отрезке [–1,1] и найти норму каждой из этих функций.

Упражнение 4. Показать, что система функций , n = 1,2,3,… является ортогональной на отрезке [–1,1] и найти норму каждой из этих функций.

§2. Ряды по ортогональным системам функций

Пусть на отрезке [a,b] задана ортогональная система функций {_n(x)}, n = 1,2,3…. Рассмотрим некоторую функцию f(x), тоже заданную на отрезке [a,b]. Если

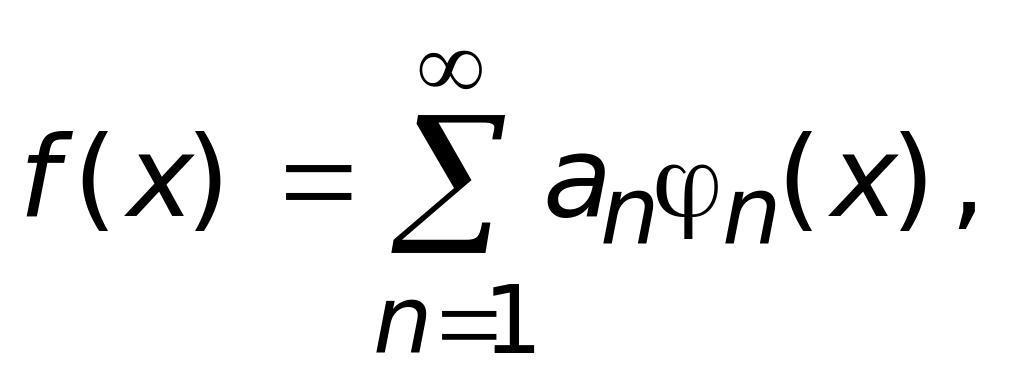(1.5)

где a_n — некоторые константы, то говорят, что функция f(x) разложена в ряд по ортогональной системе {_n(x)}. Другими словами функцию f(x) можно представить в виде бесконечной линейной комбинации функций _n(x).

В связи с этим возникают два вопроса:

1) При каких условиях f(x) можно разложить в ряд (1.5)?

2) Как найти коэффициенты a_n?

Второй вопрос решается относительно просто.

Теорема. Если функция f(x) раскладывается в ряд (1.5), то коэффициенты a_n находятся по формулам

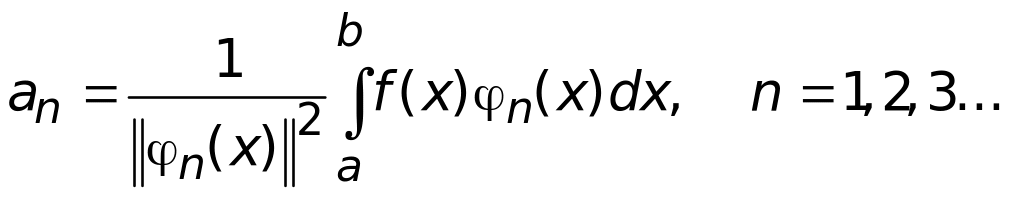(1.6)

Доказательство. Пусть функцию f(x) можно разложить в ряд (1.5), тогда умножим равенство (1.5) на _m(x) и проинтегрируем его на отрезке [a,b]

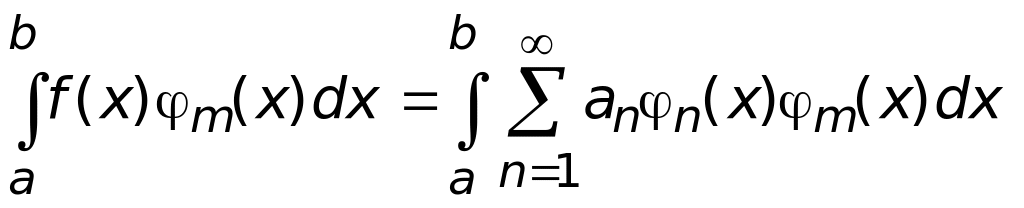. (1.7)

Поменяем местами интегрирование и суммирование, т.к. a_n — константа, ее можно вынести за знак интеграла, тогда

.

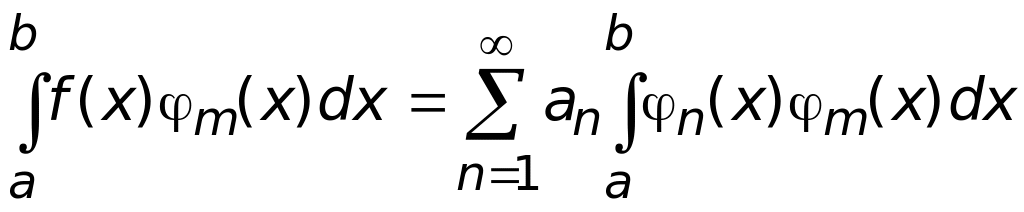Внутренний интеграл, согласно (1.2), равен нулю, если m ≠ n и ║_n(x)║², если m=n, поэтому в сумме останется только одно ненулевое слагаемое при m = n и равенство (1.7) будет иметь вид

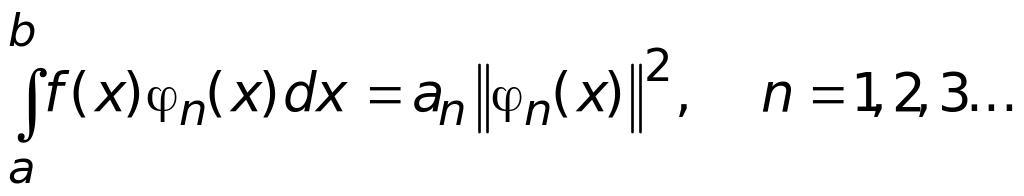
что и требовалось доказать.

Замечание. Первый вопрос достаточно сложный. Ответ на него зависит не только от функции f(x), но и от ортогональной системы функций {_n(x)}. В следующем параграфе мы дадим ответ на этот вопрос для классической тригонометрической системы функций.

Определение. Ряд 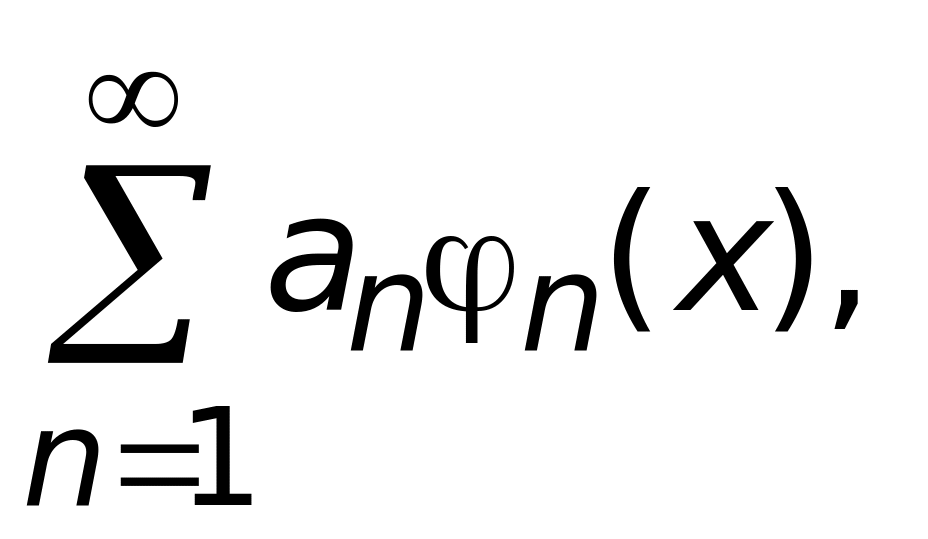называется рядом Фурье функции f(x) по ортогональной системе функций {j_n(x)}, а a_n ‑ называются коэффициентами ряда Фурье функции f(x) и вычисляются по формуле (1.6).