Тест ранговой корреляции Спирмена

Значения х_i и u_i ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

где d_i - разность между рангами х_i и u_i, i = 1, 2, ..., n;

n - число наблюдений.

Рассчитаем теоретические значения по уравнению регрессии и найдем остатки. Ранжируем совокупность по возрастанию (рисунок 3.6).

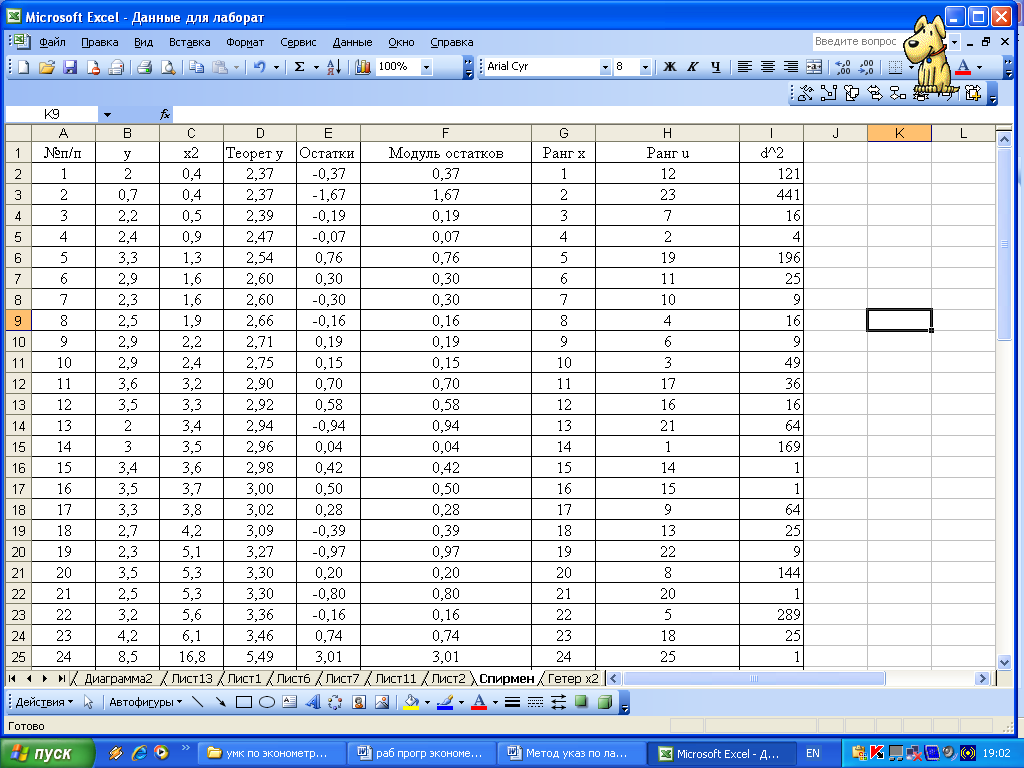
Рисунок 3.6 – Расчетная таблица для проведения теста Спирмена

Тогда .

Если коэффициент корреляции для генеральной совокупности равен нулю, то статистика

имеет распределение Стьюдента с числом степеней свободы v=n-2. Следовательно, если наблюдаемое значение t-статистики превышает табличное, то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции , а следовательно, и об отсутствии гетероскедастичности.

В нашем примере статистика Стьюдента равна:

Табличное значение статистики Стьюдента составит t(0,05; 23)=2,0687.

Таким образом, мы получили, что расчетное значение меньше табличного, следовательно, гипотеза об отсутствии гетероскедастичности принимается на уровне значимости 5%.

Аналогично проводится анализ для фактора х₃.

Тест Уайта (White test).

Тест Уайта позволяет оценить количественно зависимость дисперсии ошибок регрессии от значений фактора x, используя квадратичную функцию:

,

где - нормально распределенная ошибка.

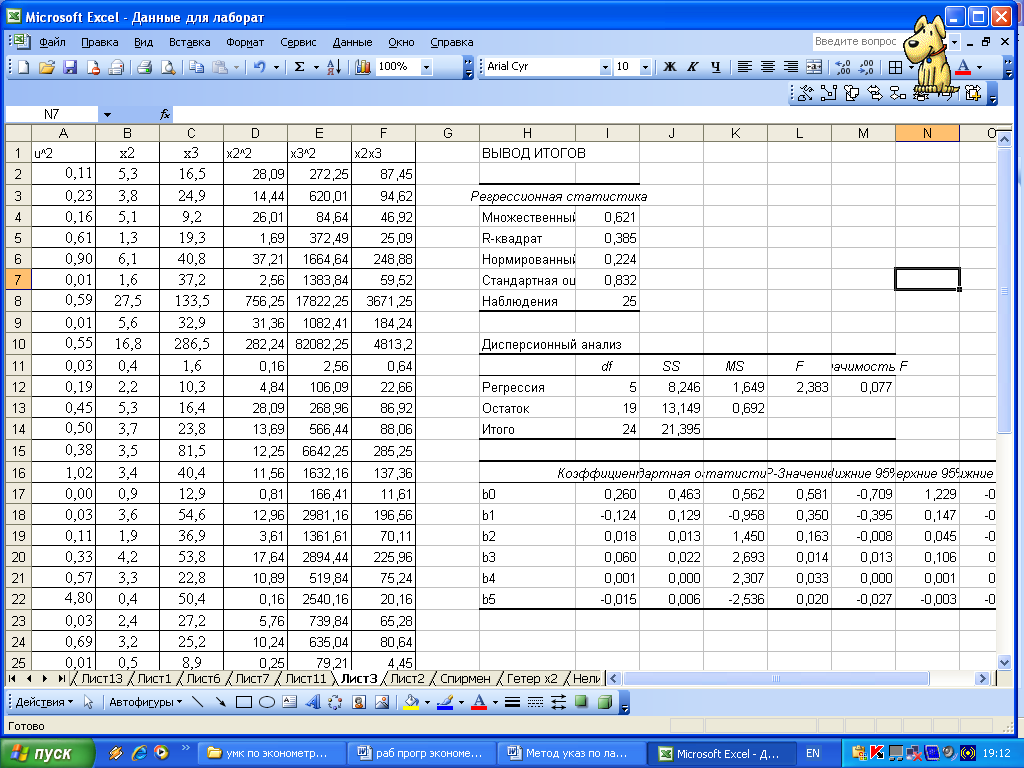
Рисунок 3.7 – Вывод итогов вспомогательной регрессии теста Уайта

Проводится этот тест следующим образом:

1. Получаем регрессионные остатки u_i;

2. Оцениваем вспомогательную регрессию;

Гипотеза об отсутствии гетероскедастичности принимается в случае незначимости регрессии в целом.

3. В нашем примере вспомогательная регрессия принимает вид:

Уравнение статистически незначимо на уровне значимости . Следовательно, гипотеза об отсутствии гетероскедастичности принимается.

2. По всем проведенным тестам можно сделать вывод о гомоскедастичности регрессионных остатков. В противном случае для устранения гетероскедастичности необходимо применить к исходным данным обобщенный метод наименьших квадратов в предположении, что .

Исходное уравнение преобразуем делением правой и левой частей на x₂: . К нему применим МНК. Полученное уравнение имеет вид: . Получены новые оценки параметров линейного уравнения, в котором смягчена гетероскедастичность.

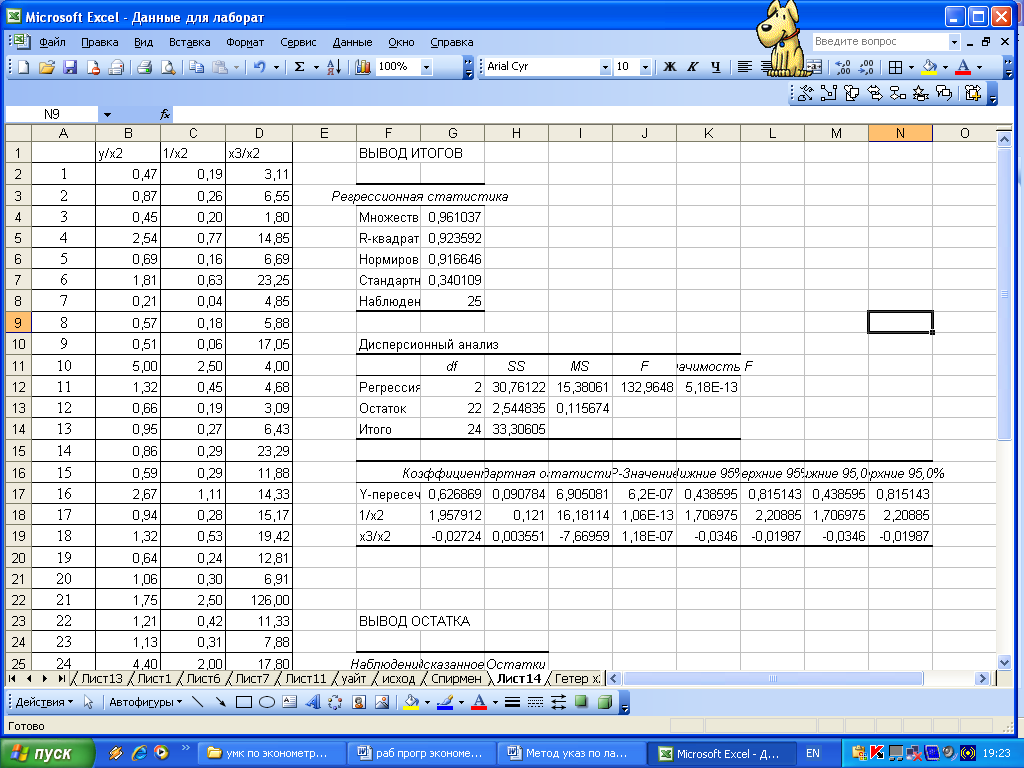
Рисунок 3.8– Вывод итога ОМНК

Задание 3

Метод рядов

Последовательно определяются знаки остатков .

Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда.

Пусть n — объем выборки;

n₁ — общее количество знаков «+» при n наблюдениях;

n₂ — общее количество знаков «-» при n наблюдениях;

k — количество рядов.

Если при достаточно большом количестве наблюдений (n₁>10, n₂>10) количество рядов k лежит в пределах от k₁ до k₂:

то гипотеза об отсутствии автокорреляции не отклоняется.

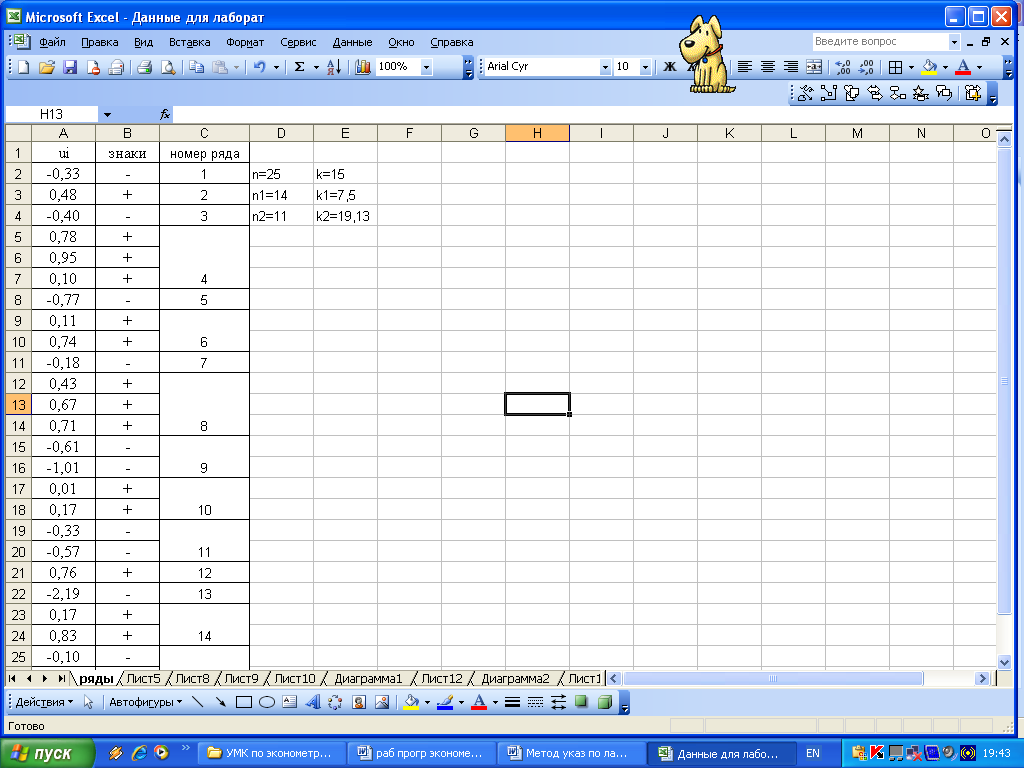
Рисунок 3.9 – Расчет характеристик метода рядов

Найдя знаки отклонений теоретических уровней от фактических, мы получили, что в анализируемой выборке содержится 15 рядов, т.е. k=15 (рисунок 3.9). Общее количество знаков «+» n₁=14, количество знаков «-» n₂=11.

Подставим найденные значения в формулу, получим, что k₁=7,5, k₂=19,13. Следовательно, гипотеза об отсутствии автокорреляции не отклоняется.