11. По полученным результатам сделайте экономический вывод.
Делается общий вывод по проделанной работе.
Лабораторная работа № 2
Регрессионные модели с переменной структурой
Задание По данным лабораторной работы 1:
1 Оцените линейную регрессию, включив в модель фиктивную переменную
2 Проверти данные на наличие структурного сдвига при помощи теста Чоу.
Реализация типовых заданий
Задание 1 По исходным данным из лабораторной работы №1, включив фиктивную переменную (таблица 2.1), построим матрицу парных коэффициентов корреляции (таблица 2.2).
Таблица 2.1 – Исходные данные для построения объединенной модели с фиктивными переменными
№ предприятия |
y |
x1 |
x2 |
x3 |
x4 |
x5 |
Пол руководителя компании |
D |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
2,5 |
38,2 |
5,3 |
16,5 |
29,4 |
1,2 |
муж. |
1 |
2 |
3,3 |
20,3 |
3,8 |
24,9 |
29 |
2 |
муж. |
1 |
3 |
2,3 |
11,4 |
5,1 |
9,2 |
27,4 |
0,9 |
муж. |
1 |
4 |
3,3 |
16,9 |
1,3 |
19,3 |
27 |
1,3 |
муж. |
1 |
5 |
4,2 |
26,9 |
6,1 |
40,8 |
25,8 |
1,6 |
муж. |
1 |
6 |
2,9 |
21,9 |
1,6 |
37,2 |
15 |
0,3 |
жен. |
0 |
7 |
5,7 |
144 |
27,5 |
133,5 |
25,5 |
2,6 |
муж. |
1 |
8 |
3,2 |
24,8 |
5,6 |
32,9 |
25,3 |
1,3 |
муж. |
1 |
9 |
8,5 |
172,3 |
16,8 |
286,5 |
24,8 |
2,3 |
муж. |
1 |
10 |
2 |
8,9 |
0,4 |
1,6 |
23,8 |
1 |
жен. |
0 |
11 |
2,9 |
13,7 |
2,2 |
10,3 |
23,8 |
1,5 |
жен. |
0 |
12 |
3,5 |
34 |
5,3 |
16,4 |
23,5 |
1,8 |
муж. |
1 |
13 |
3,5 |
20,3 |
3,7 |
23,8 |
14,7 |
1,9 |
муж. |
1 |
14 |
3 |
16,7 |
3,5 |
81,5 |
21,6 |
1,3 |
жен. |
0 |
15 |
2 |
26,4 |
3,4 |
40,4 |
21,2 |
1,5 |
жен. |
0 |
16 |
2,4 |
13,7 |
0,9 |
12,9 |
20,6 |
0,2 |
жен. |
0 |
17 |
3,4 |
33,9 |
3,6 |
54,6 |
19 |
1,1 |
муж. |
1 |
18 |
2,5 |
19,3 |
1,9 |
36,9 |
18,3 |
1,7 |
жен. |
0 |
19 |
2,7 |
24,6 |
4,2 |
53,8 |
13,9 |
2,1 |
жен. |
0 |
20 |
3,5 |
19,6 |
3,3 |
22,8 |
17,8 |
2,1 |
муж. |
1 |
Продолжение таблицы 2.1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
21 |
0,7 |
28,3 |
0,4 |
50,4 |
17,7 |
1,4 |
муж. |
1 |
22 |
2,9 |
20,4 |
2,4 |
27,2 |
17,7 |
1,8 |
муж. |
1 |
23 |
3,6 |
20,3 |
3,2 |
25,2 |
17,6 |
2 |
муж. |
1 |
24 |
2,2 |
11,1 |
0,5 |
8,9 |
16,4 |
1,3 |
жен. |
0 |
25 |
2,3 |
22,4 |
1,6 |
31,1 |
15,7 |
2 |
жен. |
0 |
Итого |
79 |
810,3 |
113,6 |
1098,6 |
532,5 |
38,2 |
- |
- |
где y – чистый доход, млрд. долл.
x1 – оборот капитала, млрд. долл.
x2 – использованный капитал, млрд. долл.
x3 – численность служащих, тыс. чел.
x4 – рыночная капитализация компаний, млрд. долл.
x5 – заработная плата служащих, тыс. долл.
Таблица 2.2 - Матрица парных коэффициентов корреляции по объединенной подвыборке
|
y |
x1 |
x2 |
x3 |
x4 |
x5 |
d |
y |
1,00 |
|
|
|
|
|
|
x1 |
0,85 |
1,00 |
|
|
|
|
|
x2 |
0,76 |
0,90 |
1,00 |
|
|
|
|
x3 |
0,83 |
0,91 |
0,71 |
1,00 |
|
|
|
x4 |
0,27 |
0,25 |
0,35 |
0,12 |
1,00 |
|
|
x5 |
0,50 |
0,50 |
0,54 |
0,43 |
-0,03 |
1,00 |
|
d |
0,39 |
0,31 |
0,36 |
0,18 |
0,40 |
0,35 |
1,00 |
По матрице коэффициентов корреляции видно, что фиктивная переменная не коллинеарна с отобранными в лабораторной работе №1 факторными переменными х2 и х3 (соответствующие коэффициенты составили 0,36 и 0,18). Следовательно можно построить модель множественной регрессии, включив эти факторы. Результаты регрессионного анализа представлены в таблице 2.3.
Модель
примет вид:
.
Уравнение регрессии значимо по F
– критерию на 5% уровне значимости. Оно
показывает, что при одном и том же объеме
использованного
капитала и численности служащих, у
предприятий руководителями которых
являются мужчины, чистый доход больше
в среднем на 0,522 млрд. долл., чем у остальных
компаний. Однако, коэффициент при D
статистически незначим (уровень
значимости составил 0,118 > 0,05).
Следовательно, влияние фактора «пол»
оказалось несущественно, и есть основание
считать, что модель одна и та же для
компаний с руководителями мужчинами и
женщинами.
Таблица 2.3 – Вывод итогов регрессионного анализа
Регрессионная статистика |
|
Множественный R |
0,881 |
R-квадрат |
0,777 |
Нормированный R-квадрат |
0,745 |
Стандартная ошибка |
0,727 |
Наблюдения |
25 |
Дисперсионный анализ |
|||||
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
3 |
38,633 |
12,878 |
24,391 |
0,000 |
Остаток |
21 |
11,087 |
0,528 |
||
Итого |
24 |
49,72 |
|
||
|
Коэффициенты |
Стандартная ошибка |
t - статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
|
1,877 |
0,244 |
7,687 |
0,000 |
1,369 |
2,385 |
|
0,522 |
0,321 |
1,628 |
0,118 |
-0,145 |
1,190 |
|
0,066 |
0,039 |
1,691 |
0,106 |
-0,015 |
0,147 |
|
0,015 |
0,004 |
4,125 |
0,000 |
0,008 |
0,023 |
Задание 2. Используя критерий Г. Чоу, выясним, можно ли считать одной и той же линейную регрессию для компаний с руководителями мужчинами и женщинами.
По 15 наблюдениям для компаний, руководителями которых являются мужчины, построим уравнение регрессии от факторов х2 и х3. Исходные данные представлены в таблице 2.4.
Таблица 2.4 – Исходные данные для построения модели по первой подвыборке (руководитель компании – мужчина)
№ п.п. |
№ предприятия |
y |
x2 |
x3 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
1 |
2,5 |
5,3 |
16,5 |
3,0 |
0,219 |
2 |
2 |
3,3 |
3,8 |
24,9 |
3,0 |
0,084 |
3 |
3 |
2,3 |
5,1 |
9,2 |
2,8 |
0,288 |
4 |
4 |
3,3 |
1,3 |
19,3 |
2,8 |
0,289 |
5 |
5 |
4,2 |
6,1 |
40,8 |
3,4 |
0,620 |
6 |
7 |
5,7 |
27,5 |
133,5 |
6,3 |
0,314 |
7 |
8 |
3,2 |
5,6 |
32,9 |
3,3 |
0,003 |
8 |
9 |
8,5 |
16,8 |
286,5 |
8,1 |
0,183 |
9 |
12 |
3,5 |
5,3 |
16,4 |
3,0 |
0,285 |
10 |
13 |
3,5 |
3,7 |
23,8 |
3,0 |
0,264 |
Продолжение таблицы 2.4
1 |
2 |
3 |
4 |
5 |
6 |
7 |
11 |
17 |
3,4 |
3,6 |
54,6 |
3,5 |
0,006 |
12 |
20 |
3,5 |
3,3 |
22,8 |
2,9 |
0,308 |
13 |
21 |
0,7 |
0,4 |
50,4 |
3,2 |
6,304 |
14 |
22 |
2,9 |
2,4 |
27,2 |
3,0 |
0,004 |
15 |
23 |
3,6 |
3,2 |
25,2 |
3,0 |
0,388 |
Итого |
54,1 |
- |
- |
54,1 |
9,559 |
|
Результаты регрессионного анализа представлены в таблице 2.5.
Таблица 2.5 – Вывод итогов регрессионного анализа по первой подвыборке
Регрессионная статистика |
|
Множественный R |
0,876 |
R-квадрат |
0,767 |
Нормированный R-квадрат |
0,728 |
Стандартная ошибка |
0,892 |
Наблюдения |
15 |
Дисперсионный анализ
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
31,431 |
15,715 |
19,730 |
0,000 |
Остаток |
12 |
9,559 |
0,797 |
||
Итого |
14 |
40,989 |
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
|
2,368 |
0,316 |
7,493 |
0,000 |
1,679 |
3,056 |
|
0,063 |
0,048 |
1,297 |
0,219 |
-0,043 |
0,168 |
|
0,016 |
0,005 |
3,441 |
0,005 |
0,006 |
0,027 |
Уравнение
примет вид:
.
Расчетные значения по нему представлены
в таблице 2.5, графа 6.
Построим модель регрессии по 10 предприятиям руководителями, которых являются женщины (исходные данные представлены в таблице 2.6).
Таблица 2.6 – Исходные данные для построения модели для второй подвыборке (руководитель компании – женщина)
№ п.п. |
№ предприятия |
y |
x2 |
x3 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
6 |
2,9 |
1,6 |
37,2 |
2,5 |
0,133 |
2 |
10 |
2 |
0,4 |
1,6 |
2,3 |
0,063 |
3 |
11 |
2,9 |
2,2 |
10,3 |
2,3 |
0,333 |
4 |
14 |
3 |
3,5 |
81,5 |
2,9 |
0,013 |
Продолжение таблицы 2.6
1 |
2 |
3 |
4 |
5 |
6 |
7 |
5 |
15 |
2 |
3,4 |
40,4 |
2,6 |
0,316 |
6 |
16 |
2,4 |
0,9 |
12,9 |
2,3 |
0,003 |
7 |
18 |
2,5 |
1,9 |
36,9 |
2,5 |
0,001 |
8 |
19 |
2,7 |
4,2 |
53,8 |
2,7 |
0,001 |
9 |
24 |
2,2 |
0,5 |
8,9 |
2,3 |
0,012 |
10 |
25 |
2,3 |
1,6 |
31,1 |
2,5 |
0,035 |
Итого |
24,9 |
- |
- |
24,9 |
0,911 |
|
Результаты регрессионного анализа представлены в таблице 2.7.
Таблица 2.7 – Вывод итогов регрессионного анализа по второй подвыборке
Регрессионная статистика
Множественный R |
0,520 |
R-квадрат |
0,271 |
Нормированный R-квадрат |
0,062 |
Стандартная ошибка |
0,361 |
Наблюдения |
10 |
Дисперсионный анализ
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
0,338 |
0,169 |
1,298 |
0,331 |
Остаток |
7 |
0,911 |
0,130 |
||
Итого |
9 |
1,249 |
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
|
2,239 |
0,218 |
10,272 |
0,000 |
1,723 |
2,754 |
|
0,001 |
0,156 |
0,009 |
0,993 |
-0,367 |
0,370 |
|
0,008 |
0,008 |
0,943 |
0,377 |
-0,012 |
0,028 |
Модель
регрессии примет вид:
.
Теоретические значения по уравнению
представлены в графе 6 таблицы 2.6.
По всем 25 предприятиям (таблица 2.8) рассчитаем уравнение регрессии для объединенной выборки.
Результаты регрессионного анализа представлены в таблице 2.9.
Таблица 2.8 – Исходные данные для построения объединенной модели с фиктивными переменными
№ предприятия |
y |
x2 |
x3 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2,5 |
5,3 |
16,5 |
2,8 |
0,107 |
2 |
3,3 |
3,8 |
24,9 |
2,8 |
0,232 |
3 |
2,3 |
5,1 |
9,2 |
2,7 |
0,163 |
4 |
3,3 |
1,3 |
19,3 |
2,5 |
0,611 |
5 |
4,2 |
6,1 |
40,8 |
3,3 |
0,902 |
6 |
2,9 |
1,6 |
37,2 |
2,8 |
0,009 |
7 |
5,7 |
27,5 |
133,5 |
6,5 |
0,590 |
8 |
3,2 |
5,6 |
32,9 |
3,1 |
0,012 |
9 |
8,5 |
16,8 |
286,5 |
7,8 |
0,550 |
10 |
2 |
0,4 |
1,6 |
2,2 |
0,033 |
11 |
2,9 |
2,2 |
10,3 |
2,5 |
0,188 |
12 |
3,5 |
5,3 |
16,4 |
2,8 |
0,455 |
13 |
3,5 |
3,7 |
23,8 |
2,8 |
0,499 |
14 |
3 |
3,5 |
81,5 |
3,6 |
0,378 |
15 |
2 |
3,4 |
40,4 |
3,0 |
1,017 |
16 |
2,4 |
0,9 |
12,9 |
2,4 |
0,000 |
17 |
3,4 |
3,6 |
54,6 |
3,2 |
0,028 |
18 |
2,5 |
1,9 |
36,9 |
2,8 |
0,107 |
19 |
2,7 |
4,2 |
53,8 |
3,3 |
0,329 |
20 |
3,5 |
3,3 |
22,8 |
2,7 |
0,572 |
21 |
0,7 |
0,4 |
50,4 |
2,9 |
4,804 |
22 |
2,9 |
2,4 |
27,2 |
2,7 |
0,029 |
23 |
3,6 |
3,2 |
25,2 |
2,8 |
0,689 |
24 |
2,2 |
0,5 |
8,9 |
2,3 |
0,009 |
25 |
2,3 |
1,6 |
31,1 |
2,7 |
0,173 |
Итого |
79 |
113,6 |
1098,6 |
79 |
12,487 |
Модель
примет вид:
.
Теоретические значения по данной модели
представлены в графе 5 таблицы 2.8.
Таблица 2.9 – Вывод итогов регрессионного анализа по всей совокупности
Регрессионная статистика |
|
Множественный R |
0,865 |
R-квадрат |
0,749 |
Нормированный R-квадрат |
0,726 |
Стандартная ошибка |
0,753 |
Наблюдения |
25 |
Дисперсионный анализ
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
37,233 |
18,616 |
32,798 |
0,000 |
Остаток |
22 |
12,487 |
0,568 |
||
Итого |
24 |
49,720 |
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
|
2,124 |
0,198 |
10,704 |
0,000 |
1,712 |
2,535 |
|
0,087 |
0,038 |
2,304 |
0,031 |
0,009 |
0,166 |
|
0,015 |
0,004 |
3,818 |
0,001 |
0,007 |
0,022 |
Рассчитываем F- критерий по формуле:
,
где
-
сумма квадратов отклонений фактических
значений результативного признака от
теоретических для объединенной выборки
(таблица 2.8, итог графы 6);
-
сумма квадратов отклонений фактических
значений результативного признака от
расчетных для первой подвыборки (таблица
2.4, итог графы 7);
-
сумма квадратов отклонений фактических
значений результативного признака от
расчетных для второй подвыборки (таблица
2.6, итог графы 7).
Табличное
значение критерия Фишера
составило 3,127. Так как расчетное значение
критерия меньше табличного, то влияние
фактора «пол» несущественно, и в качестве
оценки регрессионной модели можно
рассматривать уравнение регрессии,
полученное по объединенной выборке.
Лабораторная работа № 3
Нарушения допущений классической модели
линейной регрессии
Задания
Проведите графический анализ остатков. Проверьте остатки на гетероскедастичность с помощью:
- графического анализа,
- теста Голдфелда-Квандта,
- теста ранговой корреляции Спирмена,
- теста Уайта (White test).
Если будет обнаружена гетероскедастичность остатков, примените для исходных данных ОМНК, предполагая, что
.
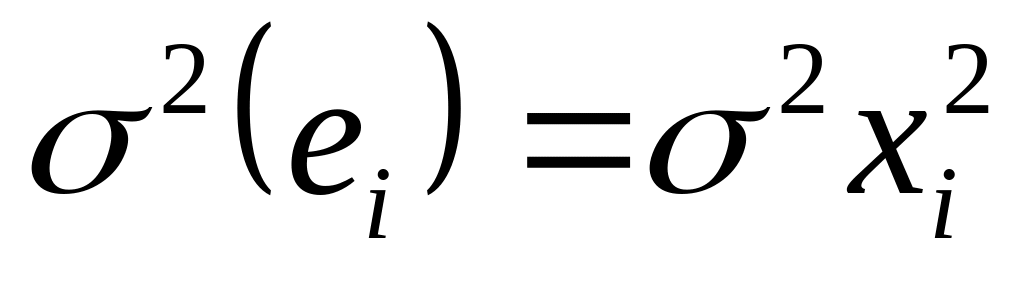3. Проверить остатки на наличие автокорреляции первого порядка, используя метод рядов, критерий Дарбина – Уотсона и Q- статистику Льюинга – Бокса. Если гипотеза об отсутствии автокорреляции первого порядка не будет отвергнута, то применить ОМНК для оценивания параметров уравнения регрессии.