5. Оцените качество уравнения через среднюю ошибку аппроксимации.
Рассчитаем среднюю ошибку аппроксимации по формуле средней арифметической простой:
Таблица 1.2 – Данные для расчета средней ошибки аппроксимации
№ п/п |
|
|
|
1 |
2 |
3 |
4 |
1 |
2,50 |
3,04 |
0,22 |
2 |
3,30 |
3,27 |
0,01 |
3 |
2,30 |
2,66 |
0,15 |
4 |
3,30 |
2,77 |
0,16 |
5 |
4,20 |
3,36 |
0,20 |
6 |
2,90 |
2,26 |
0,22 |
7 |
5,70 |
6,29 |
0,10 |
8 |
3,20 |
3,10 |
0,03 |
9 |
8,50 |
7,91 |
0,07 |
10 |
2,00 |
2,24 |
0,12 |
11 |
2,90 |
2,62 |
0,10 |
12 |
3,50 |
2,99 |
0,14 |
13 |
3,50 |
2,67 |
0,24 |
14 |
3,00 |
3,50 |
0,17 |
15 |
2,00 |
3,03 |
0,51 |
16 |
2,40 |
2,05 |
0,15 |
Продолжение таблицы 1.2
1 |
2 |
3 |
4 |
17 |
3,40 |
3,04 |
0,10 |
18 |
2,50 |
2,84 |
0,14 |
19 |
2,70 |
3,16 |
0,17 |
20 |
3,50 |
2,82 |
0,19 |
21 |
0,70 |
2,88 |
3,11 |
22 |
2,90 |
2,75 |
0,05 |
23 |
3,60 |
2,81 |
0,22 |
24 |
2,20 |
2,17 |
0,01 |
25 |
2,30 |
2,76 |
0,20 |
Итого |
79,00 |
79,00 |
6,79 |
Таким образом, фактические значения результативного признака отличаются от теоретических значений на 27,16 %. Следовательно, построенная модель является удовлетворительной.
Рассчитайте матрицу парных коэффициентов корреляции и отберите информативные факторы в модели. Укажите коллинеарные факторы.
Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии.
Парные коэффициенты корреляции рассчитываются по формулам:
;
.
Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:
1) в главном меню последовательно выберите пункты Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК;
2) заполнит диалоговое окно ввода данных и параметров вывода (рисунок 1.5);
3) результаты вычислений – матрица коэффициентов парной корреляции – представлены на рисунке 1.6.
Рисунок 1.5 - Диалоговое окно ввода параметров инструмента Корреляция
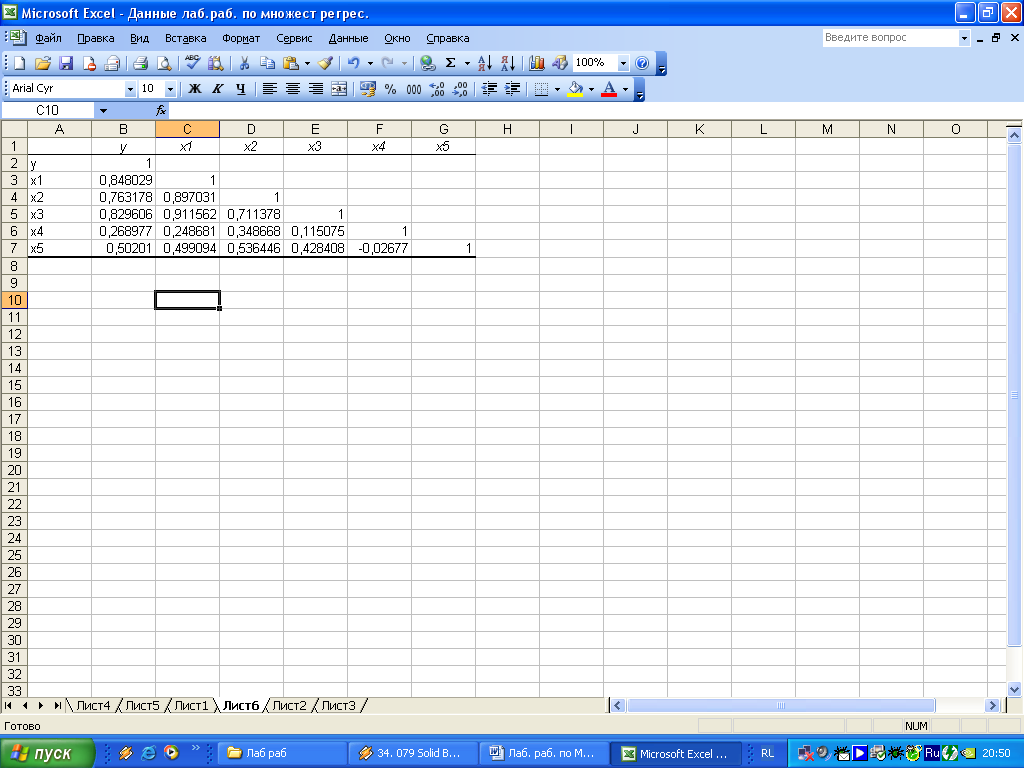
Рисунок 1.6 – Матрица коэффициентов парной корреляции
Из
матрицы можно заметить, что факторы
и
,
и
мультиколлинеарны, т.к. коэффициенты
корреляции превышают 0,75. Таким образом,
можно сказать, что они дублируют друг
друга.
При отборе факторов в модель предпочтение отдается фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В нашем примере получаем, информативными факторами являются: и .
Построим новое уравнение множественной регрессии с информативными факторами.