Построение модели ar (p) в statistica

В модуле «Временные ряды и прогнозирование» выбираем «АРПСС и автокорреляционные функции». В появившемся окне выбираем вкладку «Дополнительно». Так как ряд нестационарный его необходимо преобразовать. Используем для этого 2 способа:

1) отклонение от линейного тренда;

2) первые разности.

Рассмотрим первый способ

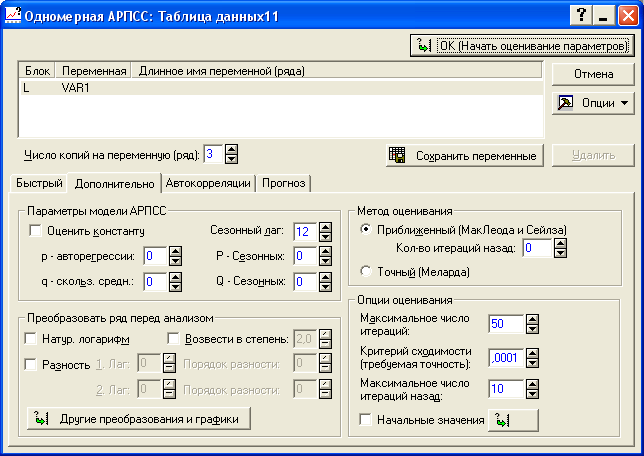
Рисунок 5.8 - Построение авторегрессионной модели

Для нахождения отклонений от линейного тренда необходимо нажать на кнопку «Другие преобразования и графики» (рисунок 5.8). В появившемся окне необходимо выбрать «Вычесть тренд» (X=X-(a+b*t)) и нажать на кнопку «OK (Преобразовать выделенную переменную)» (рисунок 5.9). На экране появится график отклонений от тренда (рисунок 5.10).

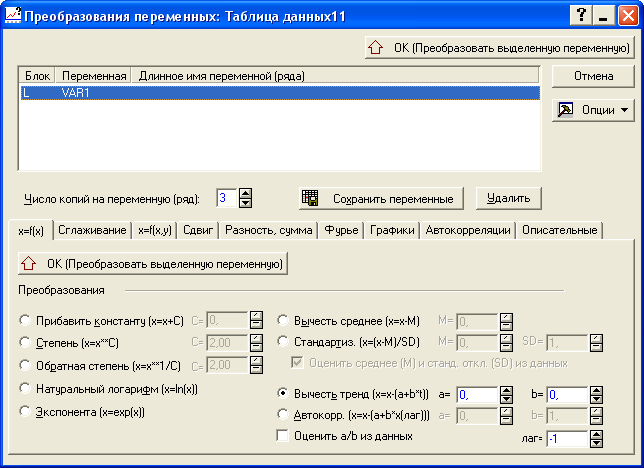
Рисунок 5.9 - Преобразование временного ряда

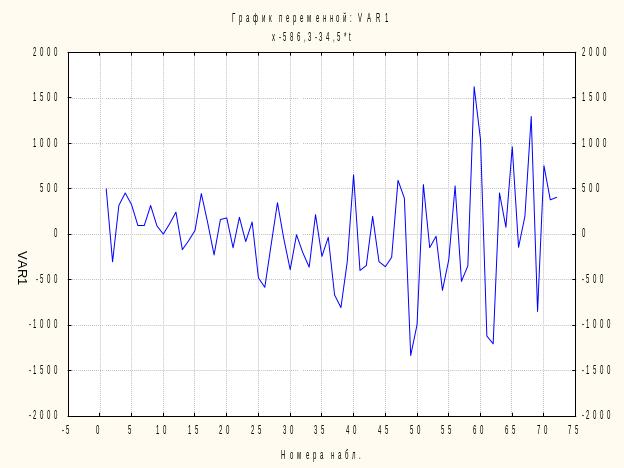
Рисунок 5.10 - Отклонения от линейного тренда

Возвращаемся в диалоговое окно «АРПСС и автокорреляционные функции», нажав на расположенную в левом нижнем углу кнопку «Другие преобразования и графики» и в появившемся окне на кнопку «Отмена».

В результате преобразования ряда появилась новая переменная VAR 1 X-586,3-34,5t (рисунок 5.11), которую мы используем в дальнейших расчетах (параметры уравнения тренда совпадает с оцененными нами ранее).

Для построения модели AR(1) в ячейке «p – авторегрессии» задаем значение порядка авторегрессии. В нашем примере p = 1 (рисунок 5.11) и нажимаем на кнопку «OK (Начать оценивание параметров)». На экране появится окно, содержащее значение параметра (рисунок 5.12). Его значение составило 0,03588 (статистически значимые параметры выделяются красным). Значение совпадает с рассчитанным нами ранее.

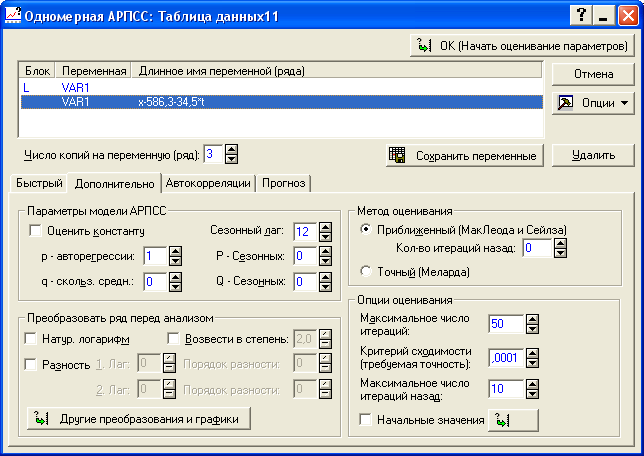
Рисунок 5.11 - Выбор порядка модели авторегрессии

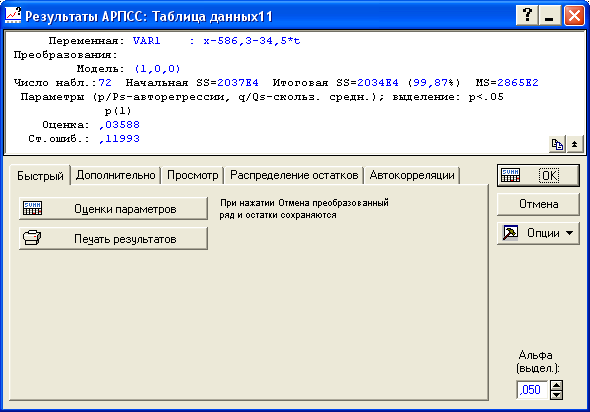
Рисунок 5.12 - Вывод итогов

Второй способ

Модель авторегрессии первого порядка по первым разностям имеет вид:

,

где , , …, - первые разности.

Для расчета ее параметров в модуле «АРПСС и автокорреляционные функции» необходимо задать порядок разности. В ячейке «Разность» устанавливаем его значение как показано на рисунке 5.13 (берем первые разности), в ячейке «p – авторегрессии» задаем значение порядка авторегрессии(p = 1) и нажимаем на кнопку «OK (Начать оценивание параметров)».

Результаты построения авторегрессионной модели по первым разностям представлены на рисунке 5.14. Параметр =-0,3105 статистически значим. Следовательно, модель примет вид:

.

В результате соответствующих преобразований получим следующую модель:

.

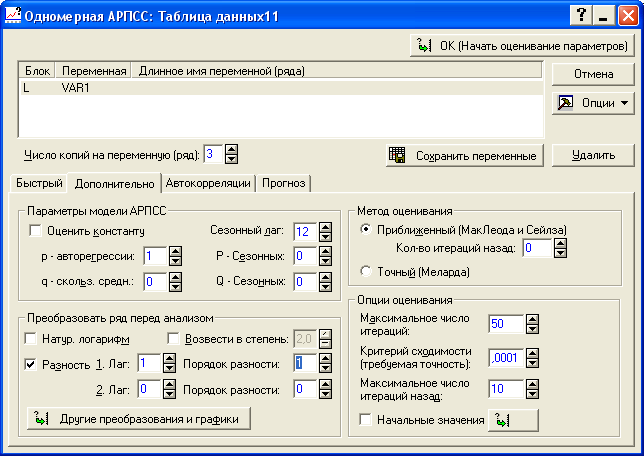
Рисунок 5.13 - Выбор параметров для построения авторегрессионной

модели

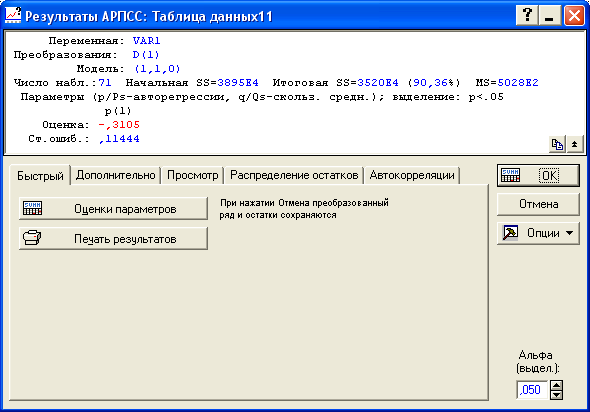
Рисунок 5.14 - Вывод итогов авторегрессионного моделирования

Лабораторная работа № 6

Системы линейных одновременных уравнений

Задание

1 Построить модель вида, рассчитав соответствующие структурные коэффициенты. Исходные данные представлены в таблице 6.1.

2 Оценить параметры модели –I Клейна, используя данные таблицы 6.2.

где - потребление;

- текущий и лаговый незарплатный доход (прибыль), долл. США;

- заработная плата работников занятых в частном секторе, долл. США;

- заработная плата работников занятых в государственном секторе, долл. США;

- запас капитала на начало года, долл. США;

- чистые инвестиции, долл. США;

- текущий и лаговый частный продукт (=НД + косвенные налоги на бизнес - );