2)Заменяем все элементы матрицы на соответствующие алгебраические дополнения : aijAij.

3)Транспонируем полученную матрицу и умножаем на коэффициент

В=А^-1

Пример:

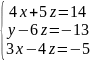
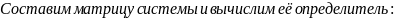
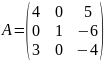; В=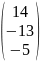

∆=-16-15=-31≠0

А^-1=-

А^-1=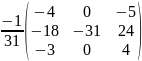

Х=А^-1*В

Х= * = =

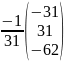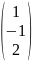
Ответ: Х⁰=

Если подставить в каждое уравнение x=1`;y=-1; z=2, то получим верные равенства.

Вывод:

1. Система совместна.

2. Имеет единственное решение.

3. Х⁰=

П⁰ 4 Решение квадратных систем по формулам Крамера.

Теорема Крамера.

Пусть имеем систему (3) А_n×n*Х_n×1=В_n×1

Рассмотрим следующие определители системы:

detA=∆=

(главный определитель системы)

и замещённые определители:

= =

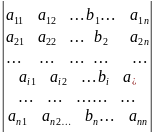b₁*A_1i+b₂*A_2i+…+b_n*A_ni

i=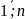

Если главный определитель системы не равен нулю, то система совместна, имеет единственное решение, которое можно найти по формулам Крамера:

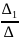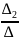(𝛂₁= ; 𝛂₂= ;...; 𝛂_n= )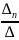

Доказательство:

Т.к. ∆≠0, то существует обратная матрица, которая имеет вид:

А^-1=

Решение системы находим по формуле: Х=А^-1*В

Х⁰= = * =

= .

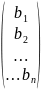Теорема доказана.

Решим предыдущий пример по формулам Крамера:

∆=-31; ∆₁=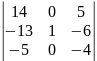 =-56+25=-31; ∆₂= =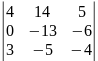

=208-252+195-120=31; ∆₃=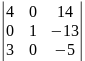 =-20-42=-62.

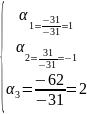
Ответ: (1; -1; 2)

Лекция 4.

п⁰5 Ранг матрицы.

Определение:

П усть дана матрица

А_m×n=

Минором «к» порядка этой матрицы называется определитель «к» порядка, составленный из элементов этой матрицы , находящихся на пересечении любых её «к» строк и «к» столбцов.

З аметим, что к≤min(m,n).

Чтобы подсчитать число всевозможных миноров «к» порядка , полученных из матрицы А_m×n используют формулу для вычисления сочетаний: N=C_m^k *C_n^k; C_m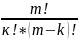^k= ; C_n^k=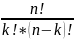 ; где n!=1*2*…*n

Пример:

А_3×4=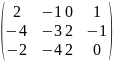 . Составим все миноры 3-го порядка.

Можно проверить, что различных миноров 3-го порядка будет ровно четыре и все они равны 0.

М_(1.2.3)^(1.2,3)=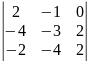 =0

(3-я строка получена суммированием 1-ой и 2-ой строк)

. М_(1.2.3)^(1.2,4)=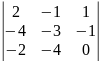 =0

(3-я строка получена суммированием 1-ой и 2-ой строк)

М_(1.2.3)^(1.3,4)= =0

(3-я строка получена суммированием 1-ой и 2-ой строк)

М_(1.2.3)^(2,3,4)=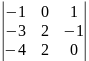 =0

(3-я строка получена суммированием 1-ой и 2-ой строк)

Рассмотрим миноры 2-го порядка .

(Таких миноров ровно 18)

Например: М_(1.2)^(1.2)=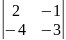 =-6-4=-10≠0

О пределение:

Базисным минором матрицы А_m×n называется любой её минор порядка «r» (r≤min(m,n) ), если он отличен от нуля, а все миноры порядка «r+1» либо равны нулю, либо не существуют.

Порядок «r» базисного минора называется рангом матрицы А, а её строки и столбцы, входящие в базисный минор , называются базисными.

Ранг нулевой матрицы принимается равным нулю.

Для ранга матрицы А приняты обозначения: r(A); rang A; rank A.

В предыдущем примере r(A)=2.

З амечание:

Напомним, что если в определителе одна из строк (столбцов) является линейной комбинацией других строк (столбцов), то определитель равен нулю. Ранг матрицы «r» определяет в матрице число линейно независимых строк (столбцов). Это означает, что в базисном миноре ни одна из строк (аналогично столбцов) не может быть получена , как линейная комбинация строк (столбцов).

r(A)=r(A^T)

Элементарные преобразования над матрицами, не меняющие её ранг.

Ранг матрицы не меняется:

1. от перестановки строк;

2. от удаления строки, являющейся линейной комбинацией других строк;

3. от удаления нулевой строки;

4. от сокращения элементов строки на общий множитель ≠0;

5. от добавления к любой строке линейной комбинации других строк.

С помощью этих преобразований любую матрицу можно привести к ступенчатой матрице:

а ₁к₁………………….а_1n a₁k₁; a₂k₂; ;a_rk_r≠0

0 …..0 a₂k₂…………..a_2n k₁k₂…k_r

0 ……..0 a₃k₃………..a_3n

……………………………..

0……………0…a_rk_r…..a_rn

Покажем, что ранг такой матрицы равен числу её строк.

Составим минор порядка «r».

М_(1,2,…,r)^(k₁,^k₂^,….,k_r⁾= =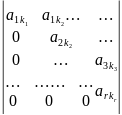

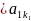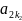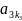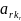* * *…* ≠0

Пример:

Найти ранг данной матрицы:

А = ~

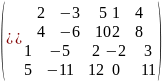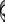
-2

~

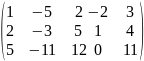
-5

~

r(A)=2

П⁰ 6. Теорема Кронекера-Капелли

.Пусть дана система линейных уравнений

(1)

или(2) А_m×n*Х_n×1=В_m×1

Если к матрице А добавить столбец свободных членов, то получим расширенную матрицу системы:

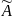=(А В)

Система линейных уравнений совместна тогда и только тогда, когда ранги матриц, а именно матрицы системы и расширенной матрицы, равны. (r(A)=r( )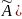

С ледствие из теоремы:

1)Система совместна  r(A)=r( ).

2)Если r(A)=r( =n, где n число неизвестных, то система имеет единственное решение.

3)Если r(A)=r( =r n, то система имеет бесчисленное множество решений, при этом «r» базисных переменных зависят от «m» свободных переменных (m=n-r)

П⁰ 7 Метод Гаусса для исследования систем линейных уравнений.

Составим расширенную матрицу системы и сведём её к ступенчатой матрице, у которой будет «r» строк.

Возможны следующие варианты:

1.r(A)=r( =r=n (ранги матриц равны и равны числу переменных)

В итоге матрица А сведётся к треугольной и система будет иметь единственное решение.

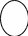
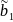
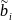
r=n

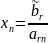
Пример 1:

+

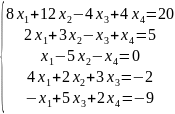
: 4

(-2)

4

= ~ ~

~

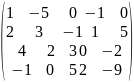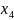
3

-5

~ ~

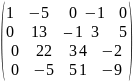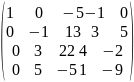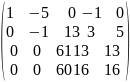
-1

-60

~ ~

~

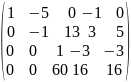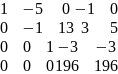
1.r(A)=r( =r=4система совместна.

2.n=4; r=4 n=r система имеет единственное решение.