§3 Системы линейных уравнений.

П⁰ 1 Линейные системы «m» уравнений с «n» неизвестными.

О пределение:

Система алгебраических уравнений имеет вид:

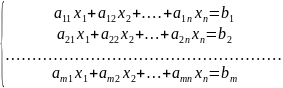
1

x₁; x₂; …;x_nнеизвестные;

a_ij коэффициенты системы; i= ; j= ;

величины b₁;b₂;…;b_m свободные члены.

Замечание 1.

Если m=n,т.е., если число уравнений равно числу неизвестных, то система называется квадратной.

Замечание 2.

Если все свободные члены равны нулю, то система называется однородной.

Определение:

Решением системы (1) называется такой набор упорядоченных чисел (𝛂₁;𝛂₂;…;𝛂_n), который при подстановке в систему (1) вместо неизвестных

x₁; x₂; …;x_n превращает её в систему верных тождеств.

Определение:

Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.

Совместная система называется определённой, если она имеет единственное решение и неопределённой в противном случае.

Исследование системы.

Исследовать систему, значит ответить на следующие вопросы:

1. Совместна система или нет.

2. Сколько решений имеет система, если она совместна.

3. Какие решения имеет система, если она совместна.

Матричная запись системы линейных уравнений.

Для системы (1) введём следующие обозначения:

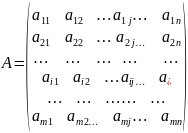матрица системы;

 матрица-столбец свободных членов;

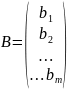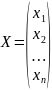
 матрица-столбец неизвестных.

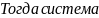(1) может быть записана в матричном виде:

2

А_m×n*Х_n×1=В_m×1

Решение такой системы можно записать в виде матрицы-столбца:

Х⁰=

П⁰ 2. Квадратные системы «n» уравнений с «n» неизвестными.

Матричный способ решения системы.

Пусть m=n, т.е имеем квадратную систему.

Р

3

ассмотрим матричную запись системы:

А_n×n*Х_n×1=В_n×1

Пусть существует обратная матрица А^-1_n×n ,т.е. А*А^-1=А^-1*А=I

Умножим обе части уравнения слева на матрицу А^-1 

А^-1*(А*Х)=А^-1*В (А^-1*А)*Х=А^-1*В  I*X=A^-1*B 

X=A^-1*B

По это формуле мы получим единственное решение системы:

Х⁰=

П⁰3 Вычисление обратной матрицы.

Теорема (о существовании обратной матрицы)

Д ля того чтобы квадратная матрица А_n×n имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т.е. определитель этой матрицы не равен нулю.

Доказательство:

Н еобходимость:

Пусть существует обратная матрица А^-1: . А*А^-1=А^-1*А=I

det(A*A^-1)=det(A)*det(A^-1)=det(I)=1det(A)≠0

(В противном случае равенство не выполняется)

Таким образом мы доказали, что если существует обратная матрица, то det(A)≠0

Достаточность:

Пусть det(A)≠0.

Докажем, что существует обратная матрица А^-1.

detA=∆=

Рассмотрим матрицу

B=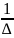 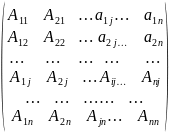, где A_ij  алгебраическое дополнение элемента a_ij матрицы А.

Докажем, что В=А^-1.

Пусть А*В=С=(с_ij)

По правилу умножения получим:

c_ij= (a_i1*A_j1+a_i2*A_j2+…+a_in*A_jn)=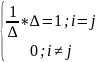

(Использовали свойства определителя)

Таким образом С=I= .

Аналогично можно проверить, что В*А=I.

Таким образом по определению обратной матрицы :А^-1=В

Теорема доказана.

Замечание:

В теореме показан вид обратной матрицы , а именно:

1)Находим определитель матрицы А (∆=detA).

(если ∆=0, то матрица вырождена и у неё нет обратной матрицы)