
- •Раздел 1. Линейная алгебра.
- •§1.Алгебра матриц.
- •I номер строки; j номер столбца, в пересечении которых стоит элемент
- •5)Диагональная матрица это квадратная матрица, у которой все элементы нестоящие на главной диагонали равны 0 (элементы главной диагонали могут принимать любые значения, в том числе и равняться 0)
- •6)Единичная матрица это диагональная матрица, на главной диагонали стоят 1.
- •7)Треугольные матрицы это квадратные матрицы, у которых ниже (верхняя треугольная матрица) или выше (нижняя треугольная матрица) все элементы равны 0.
- •Cвойства сложения.
- •Свойства умножения матрицы на число
- •П03. Умножение матриц.
- •Свойства умножения.
- •1.А*в≠в*а (свойство коммутативности не выполняется)
- •Если существуют обратные матрицы а-1 и в-1, то
- •§2 Определители квадратных матриц.
- •П02 Вычисление определителей квадратных матриц
- •Правило треугольника (Саррюса)
- •§3 Системы линейных уравнений.
- •2)Заменяем все элементы матрицы на соответствующие алгебраические дополнения : aijAij.
- •3)Транспонируем полученную матрицу и умножаем на коэффициент
- •Пример:
- •3.По данной матрице восстанавливаем систему, которая равносильна данной и найдём решение системы.
- •Пример 2:
- •3)Для нахождения общего решения по данной ступенчатой матрице восстановим равносильную систему:
- •3.Если r(a)≠r( , то система несовместна.
П02 Вычисление определителей квадратных матриц
1-го, 2-го и 3-го порядков.
1.А1=(а11)
det A1=a11
2.
A2=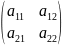
det
A2=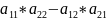
3.А3=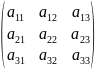
det
A3=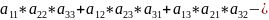
-
Правило выбора знака.
1,2,3
2,3,1
3,1,2
3,2,1
2,1.3
1,3.2

1
3
2
+0
+
+
-
-
-
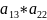 *
*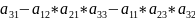
При вычислении определителей третьего порядка можно использовать следующие правила:
Правило треугольника (Саррюса)
*
*
*
*
*
*
*
*
*



+
*
*
*
*
*
*
*
*




-
Правило дописывания параллельного ряда.
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
+
1
2
3
1
2
*
*
*
*
*
*
*
*
*
*
*
*
*
*
-
П03. Вычисление определителей треугольных и диагональных матриц любого порядка.
Пусть имеем треугольную матрицу порядка «n».
А= верхняя треугольная матрица;
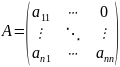
нижняя
треугольная матрица.
нижняя
треугольная матрица.
Тогда
det A=a11*a22*…*ann
Пусть имеем диагональную матрицу порядка «n».
=diag (a11;a22;…aii; ann); aij=0 если i≠j.
diag (a11;a22;…aii; ann)= a11*a22*…*ann
П04. Миноры и алгебраические дополнения элементов квадратной матрицы.
Пусть дана квадратная матрица порядка «n» Аn.
Рассмотрим определитель этой матрицы:
det A=A det(A)≠0
О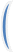 пределение
:
пределение
:
Минором
элемента
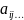 называется
определитель порядка «n-1»,
который получается из данного определителя
удалением строки и столбца на пересечении
которых стоит элемент
называется
определитель порядка «n-1»,
который получается из данного определителя
удалением строки и столбца на пересечении
которых стоит элемент
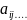 .
.
Обозначение: Мij
Пример:
∆=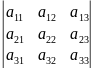 M32=
M32=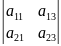
О пределение:
пределение:
Алгебраическим дополнением элемента называется минор этого элемента, взятый со знаком по формуле: (-1)n.
Аij=(-1)nMij
В нашем примере: А32=(-1)3+2М32=-
П05. Свойства определителей.
Свойство 1.
При транспонировании матрицы её определитель не меняется.
det A =det (AT)
Доказательство проведём для определителя третьего порядка.
det A= =
=
- *
det
(AT)=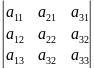 =
=
=
- * .
З амечание:
амечание:
Из этого свойства следует, что все свойства определителей, относящиеся к строкам, справедливы и для столбцов.
В дальнейшем не будем различать строки и столбцы, и именовать их рядами.
Свойство 2.
Если поменять местами два параллельных ряда, то определитель изменит знак.
Доказательство проведём для определителя третьего порядка.
∆= =
=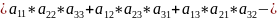
- * .
∆1= =
=
=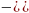
- * ).
Свойство 3.
Если в определителе два параллельных ряда равны, то определитель равен 0.
Доказательство:
Поменяем в данном определителе ∆ местами два равных ряда и получим определитель ∆1.
Тогда по свойству 2 знак поменяется, но сам определитель не изменится.
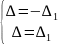 ∆=∆1=0
∆=∆1=0
Свойство 4.
Рекуррентная формула для вычисления определителя любого порядка.
Разложение определителя по элементам строки (столбца).
Определитель матрицы А равен произведению элементов какого-либо ряда на их алгебраические дополнения.
det A=ai1*Ai1+ai2*Ai2+…+ain*Ain
Доказательство проведём для определителя третьего порядка.
∆= =
а11*А11+а12*А12+а13*А13=а11 =
=
=a11(a22*a33-a23*a32)-a12*(a21*a33-a23*a31)+a13(a21*a32-a22*a31)=
(раскроем скобки и сгруппируем по знакам)
=
- * .
(Получили исходную формулу для вычисления определителя третьего порядка).
Свойство 5.
Сумма произведений элементов какого-либо ряда на соответствующие алгебраические дополнения параллельного ряда равны 0.
(Свойство аннулирования)
Доказательство проведём для определителя третьего порядка.
∆=
а
 11*А21+а12А22+а13*А23=-а11
11*А21+а12А22+а13*А23=-а11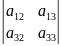 +
+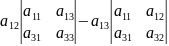 =
=
-a11*a12*a33+a11*a13*a32+a12*a11*a33-a12*a13*a31-a13*a11*a32+a13*a12*a31 =0
Свойство 6.
Если в определителе элементы какого-либо ряда равны 0, то определитель равен 0.
Действительно, разложим по элементам нулевого ряда определитель по свойству 4 и получим 0.
Свойство 7.
Определитель, в котором все элементы одного ряда являются суммой двух слагаемых, равен сумме двух определителей, например:
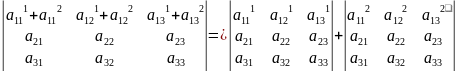
Это свойство легко проверить, если разложить определитель по соответствующему ряду по свойству 4, а в данном случае по первой строке.
Свойство 8.
Общий множитель какого-либо ряда можно выносить за знак определителя.
Доказательство проведём для определителя третьего порядка.
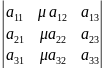 =/разложим
по второму столбцу/ =
=/разложим
по второму столбцу/ =
𝛍а12*А12+𝛍а22*А22+𝛍а32*А32=𝛍*(а12*А12+а22*А22+а32*А32)=
=𝛍 .
Свойство 9.
Определитель не изменится при элементарных преобразованиях над его рядами, т.е. если к элементам какого-либо ряда прибавить элементы параллельного ряда, умноженные на любое число.
Доказательство проведём для определителя третьего порядка.
∆=
∆1=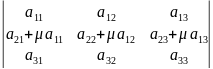 =/используем
свойства
=/используем
свойства
7, 8, 4,5/=∆+𝛍*0=∆.
Примечание:
С помощью этого свойства можно привести определитель к треугольному виду, а, следовательно, вычислять определители любого порядка.
Пример:
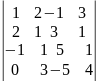 =
=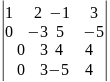 =
= =27
=27
Свойство 10.
Если одна из строк (столбцов) получена как линейная комбинация других строк (столбцов), то определитель равен 0.
Доказательство проведём для определителя третьего порядка.
∆=
Пусть S1=(a11 a12 a13)
S2=(a21 a22 a23)
S3=(a31 a32 a33)
Рассмотрим определитель :
∆1= =
=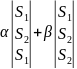 =0+0=0.
=0+0=0.
Свойство 11.
det (A*B)=det A*det B.
Пример
Вычислить определитель различными способами.
∆=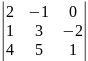
1 способ( правило треугольника)
∆=2*3*1+(-1)*(-2)*4+0-(0+(-1)*1*1+2*(-2)*5)=35
2 способ (дописывание столбцов)
∆
=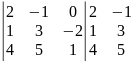 =
=
=2*3*1+(-1)*(-2)*4+0-(0+(-1)*1*1+2*(-2)*5)=35
3способ (разложение по первой строке)
∆=
=2*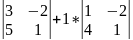 =2*(3+10)+(1+8)=35
=2*(3+10)+(1+8)=35
Лекция 3.
