
- •Раздел 1. Линейная алгебра.
- •§1.Алгебра матриц.
- •I номер строки; j номер столбца, в пересечении которых стоит элемент
- •5)Диагональная матрица это квадратная матрица, у которой все элементы нестоящие на главной диагонали равны 0 (элементы главной диагонали могут принимать любые значения, в том числе и равняться 0)
- •6)Единичная матрица это диагональная матрица, на главной диагонали стоят 1.
- •7)Треугольные матрицы это квадратные матрицы, у которых ниже (верхняя треугольная матрица) или выше (нижняя треугольная матрица) все элементы равны 0.
- •Cвойства сложения.
- •Свойства умножения матрицы на число
- •П03. Умножение матриц.
- •Свойства умножения.
- •1.А*в≠в*а (свойство коммутативности не выполняется)
- •Если существуют обратные матрицы а-1 и в-1, то
- •§2 Определители квадратных матриц.
- •П02 Вычисление определителей квадратных матриц
- •Правило треугольника (Саррюса)
- •§3 Системы линейных уравнений.
- •2)Заменяем все элементы матрицы на соответствующие алгебраические дополнения : aijAij.
- •3)Транспонируем полученную матрицу и умножаем на коэффициент
- •Пример:
- •3.По данной матрице восстанавливаем систему, которая равносильна данной и найдём решение системы.
- •Пример 2:
- •3)Для нахождения общего решения по данной ступенчатой матрице восстановим равносильную систему:
- •3.Если r(a)≠r( , то система несовместна.
Это Минор
Линейная алгебра |
Лекции по теме «линейная алгебра» |
Анисимова Н.П. |

Лекция 1.
Раздел 1. Линейная алгебра.
§1.Алгебра матриц.
п0 1.Понятие матрицы. Классификация матриц.
О пределение:
пределение:
М атрицей
размеров m×n
(m,nN)
называется прямоугольная таблица, в
каждой клетке которой находится некоторый
объект
элемент матрицы.
атрицей
размеров m×n
(m,nN)
называется прямоугольная таблица, в
каждой клетке которой находится некоторый
объект
элемент матрицы.
Если эти элементы числа, то матрица называется числовой.
Аналогично бывают и функциональные матрицы.
m- число строк; n число столбцов.
Обозначения:
А=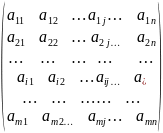 или A=(aij),
i=
или A=(aij),
i=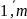 ;
j=
;
j=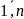 ;
;
I номер строки; j номер столбца, в пересечении которых стоит элемент
Примеры:
1)А=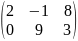 m=2;
n=3;
a23=3.
m=2;
n=3;
a23=3.
2)A=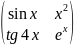 ;
m=2; n=2; a12=x2.
;
m=2; n=2; a12=x2.
Классификация матриц.
Нулевая матрица О=
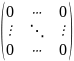 .Все
элементы этой матрицы равны 0.
.Все
элементы этой матрицы равны 0.Матрица-строка: A1×n=
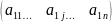 .
.
3)Матрица-столбец:
Am×1= .
.
4)Если число строк равно числу столбцов, т. е. m=n, то матрица называется квадратной матрицей порядка «n».
У


Побочная диагональ
квадратной матрицы различают две диагонали: главную и побочную.
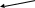
Главная диагональ


5)Диагональная матрица это квадратная матрица, у которой все элементы нестоящие на главной диагонали равны 0 (элементы главной диагонали могут принимать любые значения, в том числе и равняться 0)
 =diag
(a11;a22;…aii;
ann);
aij=0
если
i≠j.
=diag
(a11;a22;…aii;
ann);
aij=0
если
i≠j.
6)Единичная матрица это диагональная матрица, на главной диагонали стоят 1.
I=diag
(1;1;…1)=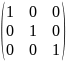 .
.
7)Треугольные матрицы это квадратные матрицы, у которых ниже (верхняя треугольная матрица) или выше (нижняя треугольная матрица) все элементы равны 0.
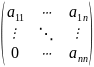 верхняя
треугольная матрица;
верхняя
треугольная матрица;
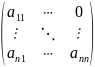
нижняя
треугольная матрица.
нижняя
треугольная матрица.
Например:
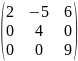
8)Пусть дана матрица Аm×n=(aij).
Транспонированной по отношению к этой матрице называется матрица, которая получается из данной заменой строк на соответствующие столбцы An×mT=(aji).
Например:
А=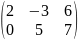 ;
АТ=
;
АТ=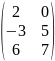 .
.
9) Квадратная матрица называется симметричной матрицей, если её элементы расположены симметрично относительно главной диагонали, т.е. aij=aji.
Примечание: Если матрица является симметричной матрицей, то она равна своей транспонированной матрице: А=АТ.
п02 Линейные операции над матрицами.
Определение 1.
Две матрицы равны тогда и только тогда, когда они одного порядка и соответствующие элементы равны, т.е.
A
 ×
×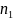 =(aij);
B
=(aij);
B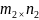 =(bij).
=(bij).
A=B
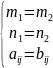
О пределение
2.
пределение
2.
Пусть даны две матрицы одного порядка. Суммой матриц называется матрица такого же порядка, что и данные матрицы, элементы которой равны сумме соответствующих элементов данных матриц.
Если Аm×n=(aij); Bm×n=(bij), то A+B=Cm×n=(cij=aij+bij)
Cвойства сложения.
1 |
А+В=В+А |
Коммутативность |
2 |
А+(В+С)=(А+В)+С |
Ассоциативность |
3 |
А+О=О+А=А |
Свойство нулевой матрицы |
4 |
Существует противоположная матрица –А: А+(-А)=(-А)+А=О |
Свойство противоположной матрицы |
5 |
Для любых матриц А и В одного порядка существует матрица С:В+С=А С=В-А (разность множеств) Cij=bij-aij |
Cсвойство обратимости |
|
|
|
О пределение
3.
пределение
3.
Пусть дана матрица Аm×n=(aij) и число 𝛂R.
При умножении матрицы А на число 𝛂 получим матрицу такого же размера как и данная матрица, при чём элементы этой матрицы получены умножением соответствующих элементов матрицы А на число 𝛂, т.е.: 𝛂*Аm×n=Cm×n=(cij=𝛂*aij)
