Системы счисления для представления числовой информации
Внутри электронной вычислительной машины (ЭВМ) информация всегда представляется в виде чисел, записанных в той или иной системе счисления.
Система счисления - совокупность приемов и правил для записи чисел цифровыми знаками. Наиболее известна десятичная система счисления, в которой для записи чисел используются цифры 0, 1, ... , 9.
Все системы представления чисел делят на позиционные и непозиционные.
Непозиционная система счисления - система, для которой значение символа не зависит от его положения в числе. Простейшие непозиционные системы с одним символом - палочкой встречались у многих древних народов. Чтобы представить какое-то число, необходимо написать столько же палочек. Ясно, что эта система неэффективна и может применяться лишь при небольших числах.
Другой непозиционной системой является римская система, в которой применяются знаки: I, V, X, L, C. Так, число 35 в римской системе счисления будет выглядеть как XXXV.
В позиционной системе счисления значение цифры определяется ее положением в числе. Например, в десятичной системе счисления в числе 222 первая цифра задает сотни, вторая - десятки, а третья - единицы.
Любая позиционная система счисления характеризуется основанием. Основание (базис) позиционной системы счисления задает количество знаков, используемых для изображения числа в данной системе.
Так, в двоичной системе счисления используются знаки 0 и 1 , в восьмеричной - символы 0,1,..., 7, в десятичной - цифры 0, 1,..., 9, в шестнадцатеричной - символы 0, 1,..., 9, A, B, C, D, E, F.
Для позиционной системы счисления справедливо соотношение
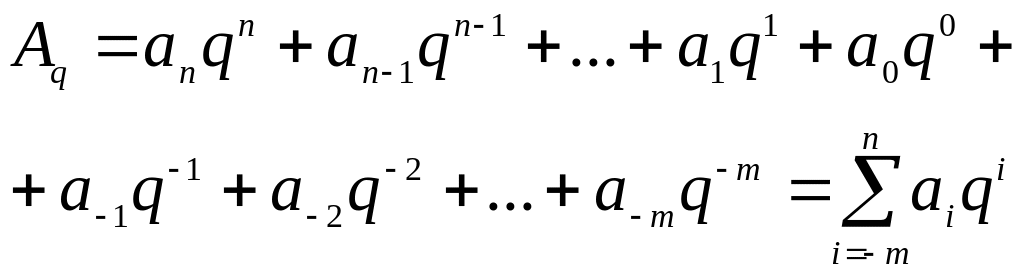
где
- произвольное
число, записанное в системе счисления
с основанием
;
n+1
и m
- число целых и дробных разрядов числа.
На практике обычно используют сокращенную
запись числа:
Примеры чисел:
в двоичной системе счисления:
,
в троичной системе счисления:
;
в восьмеричной системе счисления:
Для позиционных систем счисления характерно, что основание любой системы изображается символами 10 в своей системе.
Длина числа - количество позиций (разрядов) в записи числа. Применительно к ЭВМ обычно говорят о длине разрядной сетки ЭВМ. Для разных систем счисления требуется разное число разрядов для записи одного и того же числа: 9610 = 1408 = 101203 = 11000002 . Чем меньше основание системы счисления, тем больше длина числа. Если длина разрядной сетки задана, то это ограничивает максимальное (или минимальное) по абсолютному значению число, которое может быть записано. Пусть n - длина разрядной сетки. Тогда
.
При выборе системы счисления для представления информации внутри ЭВМ необходимо учитывать, что основание системы счисления задает число устойчивых состояний, которое должен обеспечивать элемент памяти, используемый для хранения данных в каждом разряде числа. Поэтому использовать для хранения данных внутри ЭВМ десятичную систему счисления сложно. Проще всего реализовать двоичную систему счисления, хотя в некоторых первых ЭВМ использовали и троичную систему.
Арифметические действия в двоичной системе счисления реализуются весьма просто:
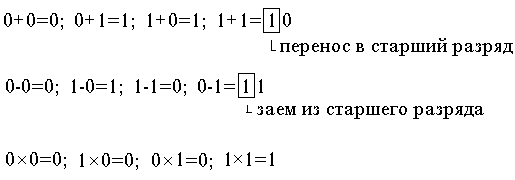
Примеры
