- •Глава 1. Усиление электрических сигналов
- •§1. Понятие об усилении электрических сигналов
- •Глава 1. Усиление электрических сигналов при помощи электронных приборов
- •§2. Принципы усиления электрических сигналов
- •Глава 1. Усиление электрических сигналов при помощи электронных приборов
- •Глава 2. Классификация усилителей
- •§1. Введение
- •Глава 2. Классификация усилителей
- •§2. Классификация усилителей
- •§3. Усилители непрерывных и дискретных сигналов
- •§4. Усилители сигналов с различными абсолютными
- •Глава 2. Классификация усилителей
- •§5. Классификация усилителей по назначению
- •§6. Классификация усилителей по виду примененных
- •Глава 3. Основные параметры и характеристики усилителей
- •Глава 3. Основные параметры и
- •§1. Основные технические показатели усилителей
- •Глава 3. Основные параметры и характеристики усилителей
- •Глава 3. Основные параметры и характеристики усилителей
- •§2. Линейные искажения
- •Глава 3. Основные параметры и характеристики усилителей
- •Глава 3. Основные параметры и характеристики усилителей
- •Глава 3. Основные параметры и характеристики усилителей
- •Глава 3. Основные параметры и характеристики усилителей
- •§3. Переходная характеристика
- •Глава 3. Основные параметры и характеристики усилителей 1, при t 〉 0
- •§4. Нелинейные искажения
- •Глава 3. Основные параметры и характеристики усилителей
- •Глава 3. Основные параметры и характеристики усилителей
- •Глава 3. Основные параметры и характеристики усилителей При усилении импульсных сигналов нелинейность усилителя
- •§5. Собственные помехи и динамический диапазон
- •Глава 3. Основные параметры и характеристики усилителей
- •Глава 3. Основные параметры и характеристики усилителей Рис. 3.13. Амплитудные характеристики усилителя: 1 – идеальная, 2 – реальная
- •Глава 4. Режимы работы усилительных элементов глава 4. Режимы работы усилительных элементов
- •§1. Режим а
- •§2. Режим в
- •Глава 4. Режимы работы усилительных элементов
- •§3. Режим с
- •§4. Режим д
- •Глава 4. Режимы работы усилительных элементов
- •§5. Точка покоя. Напряжение смещения
- •Глава 4. Режимы работы усилительных элементов
- •§6. Уравнение нагрузочного режима
- •Глава 4. Режимы работы усилительных элементов §7. Нагрузочные линии усилителя и их построение Зависимости между мгновенными значениями напряжений и
- •Глава 4. Режимы работы усилительных элементов
- •Глава 4. Режимы работы усилительных элементов
- •Глава 5. Обратная связь в усилителях Глава 5. Обратная связь в усилителях §1. Введение в общем случае ос можно определить как связь выходной
- •Глава 5. Обратная связь в усилителях
- •§2. Способы получения и виды обратной связи
- •Глава 5. Обратная связь в усилителях
- •Глава 5. Обратная связь в усилителях При подключении входа цепи ос к нагрузке rh и резистору rt ,
- •Глава 5. Обратная связь в усилителях
- •§3. Коэффициент усиления каскада и коэффициент
- •Глава 5. Обратная связь в усилителях
- •§4. Амплитудно-частотная и фазо-частотная
- •Глава 5. Обратная связь в усилителях
- •Глава 5. Обратная связь в усилителях
- •§5. Амплитудная и динамическая характеристики,
- •Глава 5. Обратная связь в усилителях
- •Глава 5. Обратная связь в усилителях
- •§6. Входное и выходное сопротивление усилителя
- •Глава 5. Обратная связь в усилителях При параллельной ос, как это следует из рассмотрения рис.
- •Глава 5. Обратная связь в усилителях
- •§7. Устойчивость работы, стабильность параметров и
- •Глава 5. Обратная связь в усилителях
- •Глава 6. Усилители на биполярных транзисторах глава 6. Усилители на биполярных транзисторах
- •§1. Однокаскадный усилитель на биполярном
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •§2. Усилители с емкостной связью
- •Глава 6. Усилители на биполярных транзисторах
- •§3. Каскад в области средних частот
- •Глава 6. Усилители на биполярных транзисторах Рис. 6.5. Статические характеристики транзистора при включении по схеме с общей базой
- •Глава 6. Усилители на биполярных транзисторах
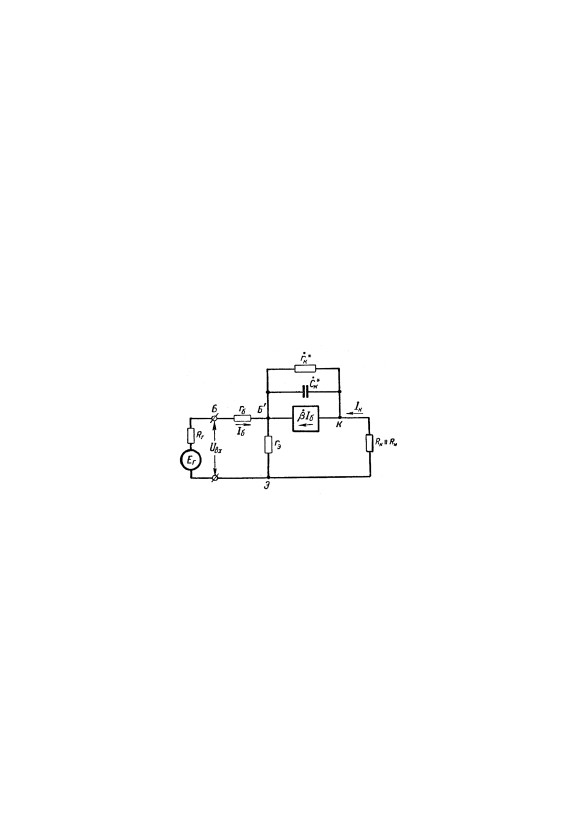
- •§4. Внутренняя обратная связь
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •§5. Полный анализ
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •§6. Каскад в области больших времен и низших частот
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •§7. Каскад в области малых времен и высших частот
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах t−
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах Время нарастания при этом выражается формулой γ э τ oe .(6.81)
- •§8. Расчет резисторного каскада на биполярном
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 6. Усилители на биполярных транзисторах III. Расчет результирующих показателей
- •Глава 6. Усилители на биполярных транзисторах
- •Глава 7. Усилители
- •§1. Введение
- •Глава 7. Усилители с обратной связью Рис. 7.2. Схема усилительного каскада с трансформаторной связью (с параллельным включением трансформатора)
- •§2. Коэффициент трансформации
- •Глава 7. Усилители с обратной связью
- •§3. Область средних частот
- •Глава 7. Усилители с обратной связью
- •§4. Область низших частот
- •Глава 7. Усилители с обратной связью
- •§5. Максимальная частота генерации транзистора
- •Глава 7. Усилители с обратной связью
- •§6. Однотактный трансформаторный усилитель мощности
- •Глава 7. Усилители с обратной связью Входной сигнал создает I bx , часть которого управляет ба-
- •§7. Двухтактные бестрансформаторные усилители
- •Глава 7. Усилители с обратной связью
- •Глава 7. Усилители с обратной связью
- •Глава 7. Усилители с обратной связью
- •§8. Расчет бестрансформаторного каскада
- •Глава 7. Усилители с обратной связью
- •Глава 7. Усилители с обратной связью 16. Емкость разделительного конденсатора в цепи нагрузки 2
- •Глава 8. Эмиттерные повторители
- •§1. Однокаскадный усилитель на биполярном
- •Глава 8. Эммитерные повторители
- •Глава 8. Эммитерные повторители §2. Динамический диапазон в отличие от обычных каскадов эп допускает работу со
- •§3. Сложные эмиттерные повторители
- •Глава 8. Эммитерные повторители
- •Глава 8. Эммитерные повторители Рис. 8.4. Составной повторитель с внутренней обратной связью Очевидно, что эквивалентное увеличение сопротивления rК 1
- •Глава 8. Эммитерные повторители Повторитель с динамической нагрузкой Как в простом, так и в составном повторителе увеличение
- •Глава 9. Операционные усилители
- •Глава 9. Операционные усилители
- •§1. Общие сведения
- •Глава 9. Операционные усилители Рис. 9.2. Принцип отрицательной обратной связи Часть выходного напряжения возвращается через цепь об-
- •§2. Идеальный операционный усилитель
- •Глава 9. Операционные усилители
- •Глава 9. Операционные усилители
- •§3. Внутренняя структура операционных усилителей
- •Глава 9. Операционные усилители
- •Глава 9. Операционные усилители Для того чтобы определить коэффициент усиления синфаз-
- •Глава 9. Операционные усилители
- •§4. Схема замещения операционного усилителя
- •Глава 9. Операционные усилители
- •Глава 9. Операционные усилители
- •§5. Коррекция частотной характеристики
- •Глава 9. Операционные усилители
- •Глава 9. Операционные усилители Подстраиваемая частотная коррекция Полная частотная коррекция операционного усилителя гаран-
- •Глава 9. Операционные усилители
- •§6. Параметры операционных усилителей
- •Глава 9. Операционные усилители Как следует из (9.16), соответствующее отклонение, приве-
- •Глава 9. Операционные усилители
- •§7. Типы операционных усилителей
- •Глава 9. Операционные усилители
- •Глава 10. Функциональные устройства на операционных усилителях глава 10. Функциональные устройства на операционных усилителях
- •§1. Линейные аналоговые вычислительные схемы на оу
- •Глава 10. Функциональные устройства на операционных усилителях то выходное напряжение определяется выражением: 1 t
- •Глава 10. Функциональные устройства на операционных усилителях Рис. 10.4. Частотная характеристика интегратора в заключение отметим, что к операционным усилителям, ра-
- •Глава 10. Функциональные устройства на операционных усилителях Устранить эти недостатки позволяет включение последова-
- •§2. Схемы линейного преобразования сигналов.
- •Глава 10. Функциональные устройства на операционных усилителях
- •Глава 10. Функциональные устройства на операционных усилителях Приравняв нулю коэффициент при u 2 , найдем условие неза-
- •Глава 10. Функциональные устройства на операционных усилителях
- •§3. Преобразователь отрицательного сопротивления
- •Глава 10. Функциональные устройства на операционных усилителях Рис. 10.13. Схема неинвертирующего интегратора Операторная передаточная функция этой цепи, определяемая
- •§4. Фильтры нижних частот
- •Глава 10. Функциональные устройства на операционных усилителях 2
- •Глава 10. Функциональные устройства на операционных усилителях
- •§5. Фильтры верхних частот
- •Глава 10. Функциональные устройства на операционных усилителях Избирательный (селективный) фильтр предназначен для вы-
- •Глава 10. Функциональные устройства на операционных усилителях
- •Глава 10. Функциональные устройства на операционных усилителях Если ачх фильтра второго порядка оказывается недоста-
- •Глава 10. Функциональные устройства на операционных усилителях §6. Измерительный усилитель на одном оу Во многих измерительных схемах необходимо измерять раз-
- •Глава 10. Функциональные устройства на операционных усилителях
- •Глава 10. Функциональные устройства на операционных усилителях
- •§7. Схемы нелинейного преобразования сигналов на оу.
- •Глава 10. Функциональные устройства на операционных усилителях
- •Глава 10. Функциональные устройства на операционных усилителях
- •§8. Прецизионные выпрямители на оу
- •Глава 10. Функциональные устройства на операционных усилителях При переходе в режим пропускания оу сначала должен вый-
- •Глава 10. Функциональные устройства на операционных усилителях
- •§9. Генераторы сигналов на оу
- •Глава 10. Функциональные устройства на операционных усилителях
- •Глава 10. Функциональные устройства на операционных усилителях Анализ схемы мультивибратора позволяет записать диффе- ренциальное уравнение: du сU − uс
- •Глава 10. Функциональные устройства на операционных усилителях
- •Глава 10. Функциональные устройства на операционных усилителях Коэффициент петлевого усиления должен, таким образом,
- •Глава 10. Функциональные устройства на операционных усилителях Рис. 10.37. Блок-схема функционального генератора Как показано на рис. 10.34, генератор прямоугольного и тре-
чение
ω H
.
Если же постоянные времени сравнимы,
то анализ пе-
реходных
и частотных характеристик усложняется.
Однако в та-
ких
главный интерес обычно представляют
не полные характерис-
тики,
а результирующий спад вершины короткого
импульса и ре-
зультирующая
граничная частота. Для оценки этих
величин можно
воспользоваться
выводами из теории ламповых каскадов.
Результирующий
спад вершины определяется формулой
(6.54),Глава 6. Усилители на биполярных транзисторах
если заменить в ней постоянную времени τ H так называем
временем спада вершины:
t
И .(6.60)t СП
Время спада, называемое иногда (менее точно) эквивалент-
ной постоянной времени цепочек, выражается в следующем виде:
δ≈
t СП
m 1
= ∑
i =1 τнi
,
−1
(6.61)
где τ нi – постоянная времени i -й цепочки.
В распространенном случае, когда все m постоянные вре-
мени одинаковы, получаем:
t СП =
τн
.
m
(6.62)
Значит, по заданным значениям δ и t И нужно найти необхо-
димое время t СП и затем рассчитать каждую емкость из соотно-
шения τ н = mt СП . В каскаде на рис. 6.3, очевидно, m = 3 .
Результирующая граничная частота ω н 0 на уровне 0,7 не
имеет достаточно простой связи с граничными частотами отдель-
ных цепочек ω нi . Однако весьма приближенно ее можно оценить,
заменив в формулах (6.61) – (6.62) величины τ нi на 1 ωнi (что
– 105 –

Л.В.
Кропочева. «Усилительные устройства»
вполне
строго) и величину t СП
на
1 ω н
0 (что
и является причиной
неточности).
Тогда в общем случае
ω
н
0 ≈
∑
ω
нi
,
i
=1
m
(6.63)
а
в частном случае, когда все ω нi
одинаковы,
ω
Соотношения (6.63) – (6.64) гораздо более точны тогда, ког-
да граничные частоты определяются на уровне более высоком,
чем 0,7, например, на уровне 0,9.
Коррекция искажений вершины
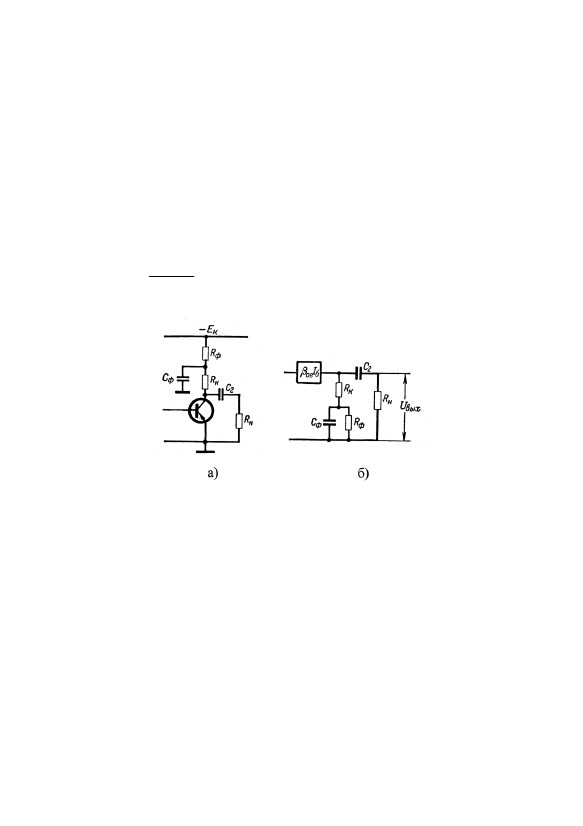
Для уменьшения спада вершины можно принять RC -фильтр
в коллекторной цепи (рис. 6.9). Этот способ хорошо известен из
ламповой техники. Поэтому, не проводя детального анализа, ука-
жем лишь его предпосылки. Записав в операторной форме выход-
ное напряжение, нетрудно получить следующее изображение для
коэффициента усиления:
1+
K u ( s) = K u 0
1+
α
Ф1 + sτ ф
α′1
ф+sτ н 1 + sτ ф
.
Здесь τ ф
= С ф Rф ; τ н = С 2 R H ; α ф = R ф R K ; α ′ = R ф (R H + R K ) .ф
Умножая числитель и знаменатель дроби на 1 + sτ ф / sτ ф , а
затем деля числитель на знаменатель с точностью до членов вто-
рого порядка относительно 1 s , получим изображение вида
(
)
a
2 aK u ( s ) = K u 0 1 + 1 + 2
s s
.
– 106 –
Полагая
здесь aГлава 6. Усилители на биполярных транзисторах
ны, при котором отсутствует линейный спад в начале выходного
импульса. Это условие оказывается таким же, как и в случае лам-
пового каскада:
C ф RК = C 2 RH .
(6.65)
Отсюда определяют емкость фильтра C ф . При выполнении
условия (6.65) спад вершины будет квадратичным, а величина
относительного спада в конце импульса будет выражаться фор-
мулой δ =
2
tИ2α ф τ 2н
, где t И – длительность импульса.
Рис. 6.9. Принципиальная (а) и эквивалентная (б) схемы каскада с
коллекторным фильтром для коррекции искажений вершины импульса
Эта формула тоже совпадает с соответствующим выраже-
нием для лампового каскада. Таким образом, специфика транзи-
сторного каскада (в котором в отличие от лампового не имеет
места неравенство R H 〉〉 R K , R ф ) не проявляется при соблюдении
условия коррекции. В тех случаях, когда условие (6.65) не выпол-
няется, переходная характеристика транзисторного каскада име-
ет некоторую специфику, однако этот вопрос является частным и
мы на нем не будем останавливаться.
– 107 –