Порядок виконання роботи

Розглянемо приклад виконання практичної роботи (у прикладі розраховується внутрішня швидкість обігу та оцінюється економічна доцільність для одного проекту. Аналогічно у завданні знаходиться внутрішня швидкість обігу для другого і третього проектів, і три проекти порівнюються між собою).

Припустимо, що витрати з проекту складають 500 млн грн. Доходи упродовж чотирьох наступних років становлять 50 млн грн, 100 млн грн, 300 млн грн, 200 млн грн. Оцінити економічну доцільність проектів за швидкістю обігу інвестицій, якщо ринкова норма доходу становить 12 %.

Нехай клітинки В2:В6 містять значення -500 (витрати з проекту є від'ємним числом, тому що показують вкладення грошей), 50, 100, 300, 200. Внутрішня швидкість обігу інвестиції складає: ВНДОХ (В2:В6) = 9,25 %.

Це менше ринкової норми, тому проект є економічно недоцільним. Інвестиція розміром 500 млн грн (від’ємне значення на графіку) принесе доходи в наступні чотири роки, які показані на графіку додатними значеннями, сумарна величина яких більше первісних витрат, але поточна вартість дорівнює їм при швидкості обігу інвестиції 9,25 %.

Графічний приклад виконання завдання наведено в Додатку Б.

Контрольні питання

1. Особливості використання фінансово-інвестиційних операцій.

2. Особливості видів фінансово-інвестиційних функцій та їх застосування до конкретних прикладних задач.

Практична робота № 4

Тема. Основні властивості задач лінійного та динамічного програмування

Мета: розрізняти поняття програми, програмованих та непрограмованих рішень, знати моделі лінійного та нелінійного програмування, розрізняти моделі динамічного програмування

Завдання № 5 Задача про оптимальну заміну обладнання

Мета: вивчити і вміти застосовувати функції динамічного програмування та оптимізації.

Завдання до роботи: необхідно розв'язати запропоновану задачу за даним зразком. Початкові дані для розрахунку задачі наведено в таблиці 9+N, де N – останні дві цифри номера залікової книжки студента.

Короткі теоретичні відомості

Однією з важливих економічних проблем є вибір оптимальної стратегії при заміні старого обладнання (верстати, машини, агрегати, виробничі будови і т.д.) на нове. Розглянемо плановий період, що складається з декількох років, на початку якого є обладнання фіксованого віку. У процесі експлуатації обладнання дає щорічний дохід, вимагає експлуатаційних витрат і має залишкову вартість, причому всі перераховані характеристики залежать від віку обладнання.

У будь-який рік обладнання можна або зберегти, або продати за залишковою вартістю і купити замість нього нове, за відомою ціною, що теж може змінюватися з часом.

Задача полягає в тому, щоб для заданого планового періоду визначити оптимальну (за сумарним прибутком) стратегію поведінки (заміна чи збереження) щодо цього устаткування.

Підкреслимо, що в такій постановці – це задача максимізації. Якщо ж за критерій оптимальності взяти умову, що сумарні витрати на експлуатацію обладнання повинні бути мінімальними, то одержимо задачу мінімізації.

Основною характеристикою обладнання, тобто параметром стану, є його вік ( – вік нового обладнання). При побудові динамічної моделі задачі процес заміни обладнання розглянемо як кроковий, розбиваючи весь період експлуатації на кроків.

Уведемо позначення:

– вартість продукції, виготовленої за 1 рік на обладнанні віку років;

– щорічні експлуатаційні витрати на обслуговування обладнання віку років;

– залишкова вартість обладнання віку років;

– закупівельна вартість нового обладнання;

– тривалість планового періоду.

Для розв’язання задачі використовуємо принцип оптимальності Р. Беллмана. Розглянемо роки планового періоду, починаючи від кінця до початку. Уведемо функцію умовно-оптимальних значень критерію оптимальності , що відповідає максимальній величині прибутку, отриманого від експлуатації обладнання віку років за останні кроків планового періоду. Вік обладнання розглядається в напрямку природного перебігу часу, тобто відповідає використанню нового обладнання. Часові кроки нумеруються у зворотному напрямку, тобто означає, що розглядається останній рік планового періоду. Напрями зміни і показані на рисунку 3.

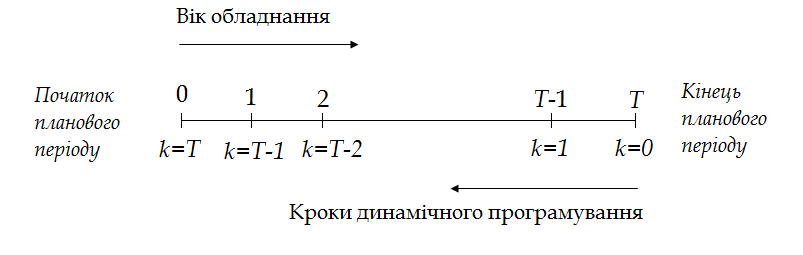
Рис. 3 – Напрями зміни часу і кроків динамічного програмування

Процес розв’язання починаємо з останнього кроку. На початок останнього року, тобто для , зробимо всі можливі припущення. Нехай при вік обладнання дорівнює рокам. На початку го інтервалу маємо дві можливості: замінити обладнання або зберегти його. Якщо обладнання зберігаємо, то прибуток у період дорівнює ; якщо обладнання замінюємо на нове, то одержимо прибуток рівний . Оптимальною для періоду буде така стратегія, що забезпечує найбільший прибуток за цей період. Інакше кажучи, якщо виконується умова , то обладнання доцільно замінити, а у випадку виконання нерівності його вигідно зберегти.

Таким чином, одержуємо перше функціональне рівняння

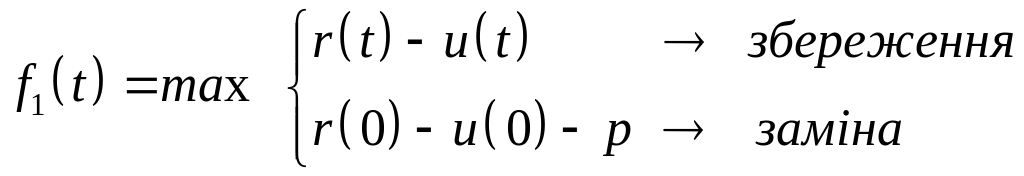(1)

Для розглядаємо прибуток за останні два роки: і . Оскільки вже визначені оптимальні дії, які забезпечують максимум доходу , то для стратегії збереження обладнання розрахункова формула доходу за два останніх роки має вигляд , для стратегії заміни обладнання маємо . Умовно оптимальною протягом останніх двох років буде стратегія, що забезпечує максимум прибутку

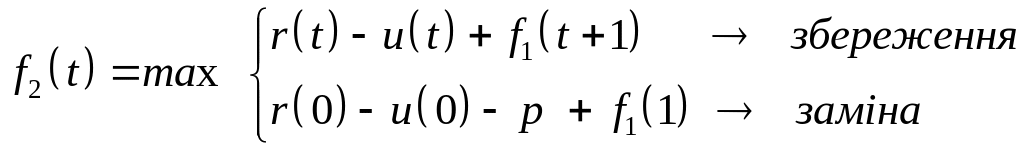(2)

Аналогічні міркування справедливі і для всіх інших кроків. Загальне функціональне рівняння для обчислення умовно оптимального прибутку для го кроку можна записати у вигляді

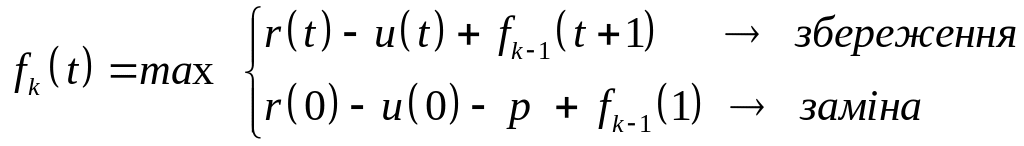(3)

Для останнього кроку одержимо максимальний прибуток

(4)

Співвідношення (1)–(4), що встановлюють зв’язок між і , називаються рекурентними співвідношеннями.