Контрольні питання

1. Дайте визначення поняття «дерево рішень».

2. Сформулюйте етапи побудови «дерева рішень».

Практична робота № 9

Тема. Багатофакторний регресійний аналіз

Мета: Знаходження двофакторної моделі лінійної регресії*. Використання пакета «Анализ данных» для розрахунку параметрів парної і багатофакторної регресії.

Завдання № 14 Функції для роботи з лінійною регресією. Функція ТЕНДЕНЦИЯ.

Короткі теоретичні відомості

Якщо функція ЛИНЕЙН повертає математичний опис прямої лінії, яка апроксимує відомі дані, то функція ТЕНДЕНЦИЯ (TREND) дає можливість визначити точки, які лежать на цій лінії. Масив чисел, який повертає функція ТЕНДЕНЦИЯ, можна використовувати для побудови лінії тренду – прямої лінії, яка допомагає зрозуміти поведінку фактичних даних. Крім того, ця функція дозволяє апроксимувати дані, тобто будувати прогноз майбутніх значень на основі тенденції, виявленої для відомих даних.

Функція ТЕНДЕНЦИЯ має чотири аргументи:

ТЕНДЕНЦИЯ (известные_значения_у; известные_значения_х; новые_значения_х; конст)

Перші два аргументи – це відомі значення залежних і незалежних змінних відповідно. Як і в функції ЛИНЕЙН, аргумент известные_значения_у є одним стовпчиком, одним рядком чи прямокутним діапазоном. Третій та четвертий аргументи не є обов’язковими.

Для визначення лінії тренду, яка апроксимує відомі дані, просто опустимо третій та четвертий аргументи в цій функції. Масив результатів буде мати той самий розмір, що і діапазон известные_значения_х.

Порядок виконання роботи

Завдання А. Використовуючи дані про обсяги експорту продукції підприємства наведені на рисунку 14 та функцію ТЕНДЕНЦИЯ знайти точки на лінії регресії, яка апроксимує множину даних.

Хід роботи

1. Виділимо діапазон С2:С16.

2. Уведемо формулу (для введення формули доцільно скористатися майстром функцій, функція ТЕНДЕНЦИЯ знаходиться в категорії Статистические):

=ТЕНДЕНЦИЯ(В2:В16; А2:А16)

3. Натискаємо одночасно клавіші Сtrl+Shift+Еnter для вводу даної формули як формули масиву.

4. Результат виконання частини завдання подано на рисунку 15.

Використовуючи дані про обсяги експорту продукції підприємства наведені на рисунку 14 та функцію ТЕНДЕНЦИЯ здійснити екстраполяцію на 17, 18 та 19 місяці, або визначити обсяги експорту в ці місяці.

Завдання Б. Для екстраполяції на основі даних, що є в нашому розпорядженні, ми повинні задати аргумент новые_значения_х, під який можна відвести будь-яку кількість клітинок. Масив результатів буде такого самого розміру, що і діапазон новые_значения_ х.

Хід роботи:

1. У клітинки А18:А20 введемо числа від 17 до 19.

2. Виділимо діапазон С18:С20 і введемо наступну формулу як формулу масиву: =ТЕНДЕНЦИЯ(В2:В16; А2:А16; А18:А20).

3. Результат виконання цієї частини завдання подано на рисунку 15.

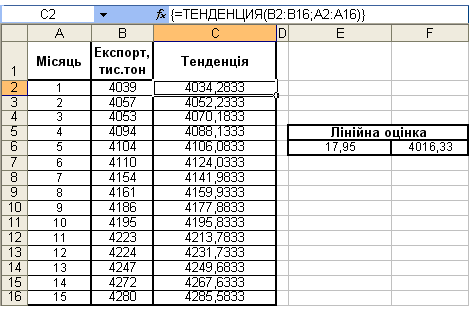
Рисунок 14 – Функція ТЕНДЕНЦІЯ створює ряд даних, який може

бути відображений у вигляді лінії на діаграмі

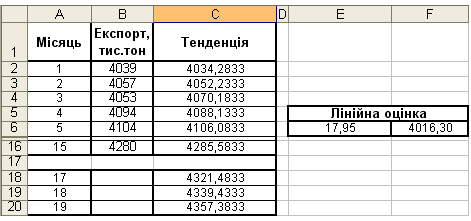
Рисунок 15 – Прогнозування обсягів експорту на 17, 18 та 19 місяці за допомогою функції ТЕНДЕНЦІЯ

Завдання № 14 Функції для роботи з лінійною регресією. Функція Предсказ

Короткі теоретичні відомості

Функція ПРЕДСКАЗ (FORECASТ) аналогічна функції ТЕНДЕНЦИЯ за винятком того, що вона повертає одну точку даних на лінії регресії, а не масив, який визначає цю лінію.

Ця функція має наступний синтаксис:

= ПРЕДСКАЗ (х; известные_значения_у; известные_значения_х)

Аргумент х – це точка даних, для якої ви бажаєте виконати екстраполяцію.

Порядок виконання роботи

Використовуючи дані про обсяги експорту продукції підприємства наведені на рисунку 16 та функцію ПРЕДСКАЗ знайти точки на лінії регресії, які відповідають значенням х рівним 18 і 19.

Хід роботи

1. У клітинку E19 уведемо наступну формулу:

=ПРЕДСКАЗ(А19; В2:В16; А2:А16)

2. Можна використати й інший синтаксис написання даної формули:

=ПРЕДСКАЗ(А18; В2:В16; А2:А16)

3. Тут аргумент х вказує на 18 точку даних на лінії регресії.

4. Аналогічні дії виконаємо і для клітинки E20.

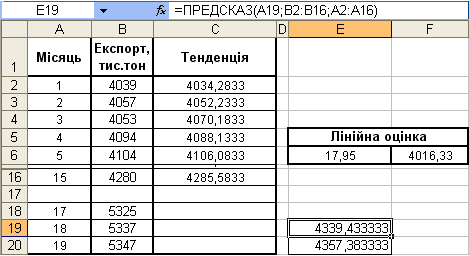
Рисунок 16 – Прогнозування обсягів експорту на 18 та 19 місяці

за допомогою функції ПРЕДСКАЗ

Завдання № 15 Використання пакета АНАЛИЗ ДАННЫХ для розрахунку параметрів парної і багатофакторної регресії

Даний пакет використовується для розрахунку параметрів парної і багато факторної регресії методом найменших квадратів (1МНК), а також для оцінки тісноти та значущості зв’язку між змінними при проведенні дисперсійного або кореляційного аналізу.

Порядок виконання роботи

Алгоритм дій для реалізації багатофакторної регресії продемонструємо на прикладі (рис. 17). Вводимо вихідні дані на ЛИСТ, як показано на рис. 17.

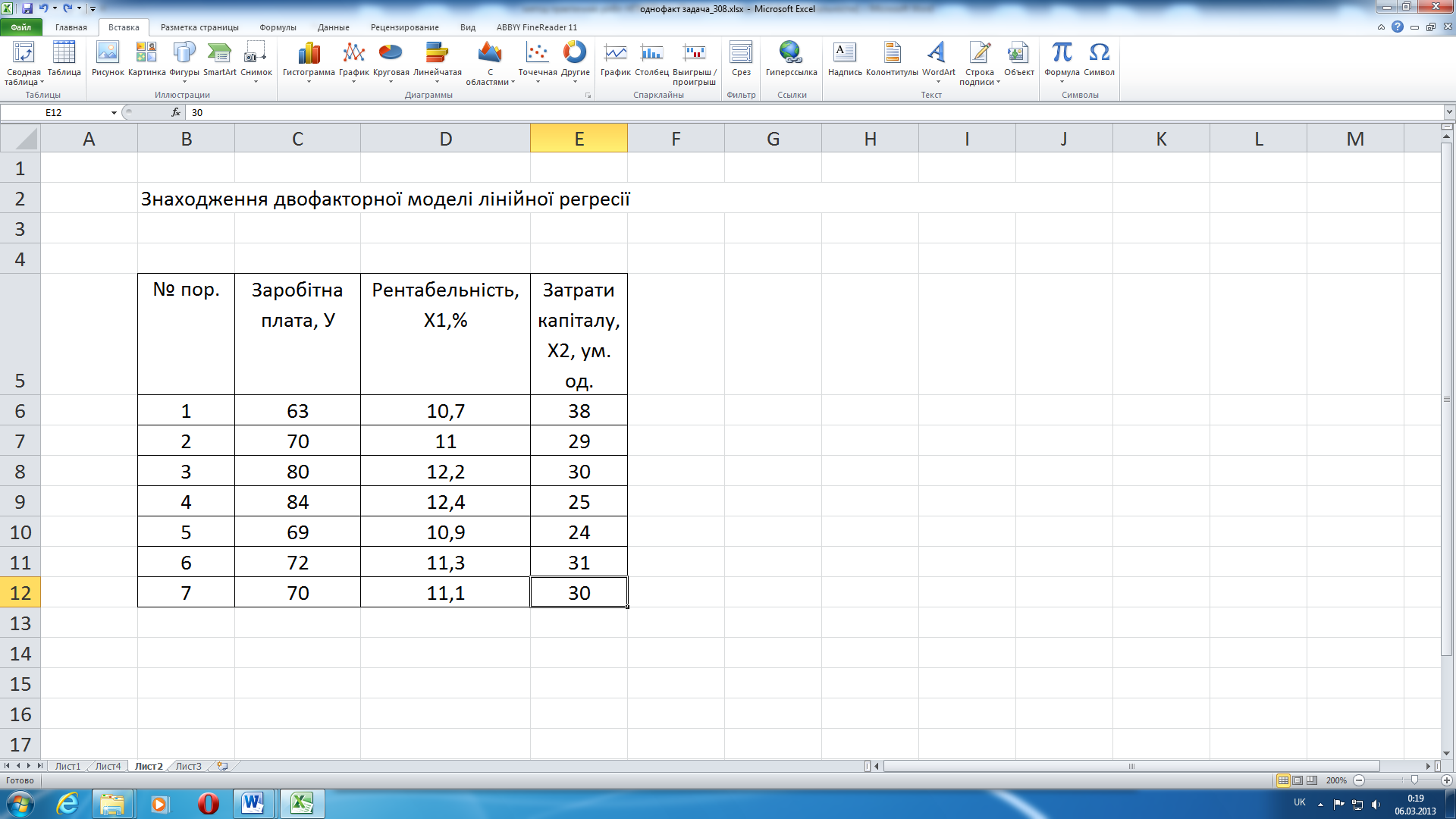
Рис. 17 – Вхідні дані

Для регресійного аналізу в MS Excel можна також застосовувати пакет аналізу: <Сервис>, <Анализ данных>, <Регрессия> (або <Данные>, <Анализ данных> ) (рис. 18).

Рисунок 18 – Меню вибору методу аналізу

Вводимо параметри у вікні регресійного аналізу (рис. 19).

Входной интервал Y – діапазон значень залежної змінної Y.

Входной интервал X – діапазон значень незалежних змінних X.

Метки – якщо в діапазон даних включено заголовки стовпчиків потрібно поставити позначку.

Константа ноль – вказує на наявність чи відсутність константи в регресії.

Уровень надежности – рівень достовірності, стандартно 95 %.

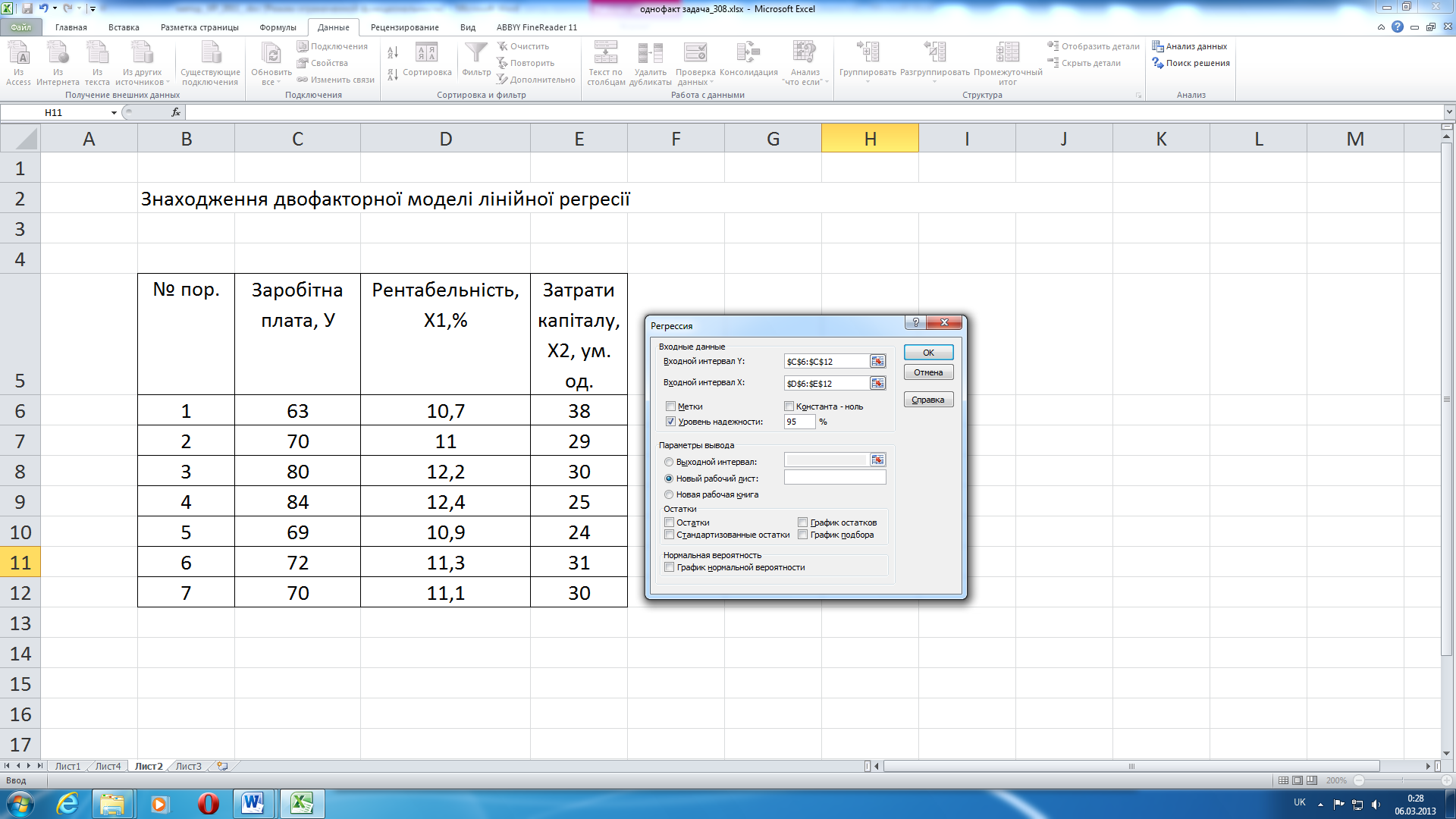
Рисунок 19 – Параметри регресійного аналізу

Параметры вывода – вибираємо, де мають виводитись результати аналізу: на поточному робочому листі, новому чи у новому файлі. Рекомендується «Новый рабочий лист», де можна задати ім’я робочого листа.

На новому робочому листі з’являються результати аналізу, у вигляді таблиці, яка складається з 3 складових (рис. 20).

Значення виведених показників аналізу моделі наводимо нижче.

Регресійна статистика

Множественный R – коефіцієнт множинної кореляції;

Коефіцієнт множинної кореляції R свідчить про зв’язок усіх незалежних змінних і результуючої змінної у випадку, якщо його значення перевищує 0,7. Таким чином, зв’язок між заробітною платою, рентабельністю та затратами капіталу, є тісним, оскільки коефіцієнт множинної кореляції R = 0,9966.

R-квадрат – квадрат коефіцієнта кореляції (коефіцієнт детермінації), показує ступінь пояснення експериментальних даних моделлю.

Коефіцієнт детермінації R² вказує на те, яка частка варіації поясненної змінної зумовлена варіацією змінної, що її пояснює ( ). Чим ближче R² до одиниці, тим краще регресія апроксимує емпіричні дані. Якщо R² = 1, то між Х і У існує функціональна залежність, тоді як R² = 0 свідчить про те, що пояснена зміна не залежить від обраного набору змінних. Для отриманої моделі даний показник становить 0,9933. Тобто отримана модель на 99 % пояснює зміну заробітної плати.

Нормированный R-квадрат має зміст «песимістичного прогнозу» R-квадрату.

Нормований (скоригований чи адаптований) коефіцієнт детермінації визначається таким чином:

= 0,9900,

де n – кількість спостережень; m – кількість параметрів.

На відміну від R² може зменшуватись при введенні в модель нових змінних, що пояснюють, але не здійснюють істотного впливу на залежну зміну, тоді як R² таких випадках збільшується.

Стандартная ошибка – середньоквадратичне відхилення моделі (для нашої моделі = 0,7128).

Наблюдения – кількість експериментальних точок (для нашої моделі це 7).

Дисперсійний аналіз

df – кількість ступенів свободи: на регресію, залишкова та загальна (для нашої моделі це: регресійної (m-1= 2); залишкової (n- m =7-3=4); загальної (n-1=7-1=6); SS – сума квадратів відхилень між експериментальними та розрахованими згідно з моделлю значеннями. Комірка С12 містить пояснену суму квадратів, зумовлену регресією.

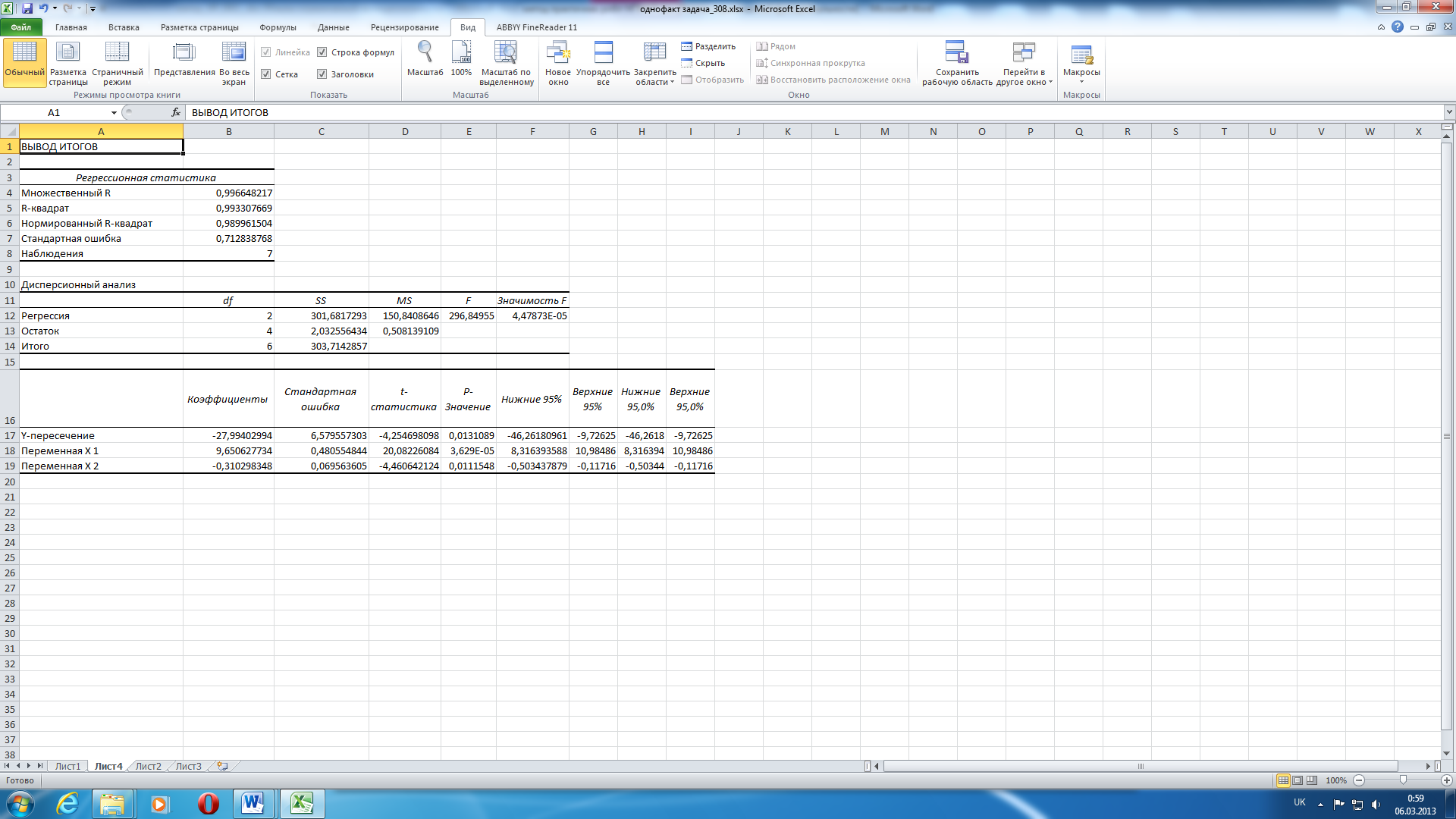
Рис. 20 – Результати регресійного аналізу

69

Комірка С13 містить залишкову суму квадратів, що пояснює відхилення від регресії. Метод найменших квадратів полягає у виборі такого набору коефіцієнтів серед усіх можливих, який забезпечує мінімальне значення SS oст. MS – дисперсія; F – F-статистика. Вибіркове значення F, що має розподіл Фішера, у комірці Е12 застосовується для оцінки значущості коефіцієнта детермінації R². Значимость F – показує ймовірність можливості хибного висновку на основі одержаних даних.

F і значущість F дозволяють перевірити значущість рівняння регресії, тобто встановити відповідність результатів регресійної моделі емпіричним даним і достатність незалежних змінних, внесених до неї, для опису залежної змінної.

За емпіричним значенням статистики F перевіряється гіпотеза рівності нулю всіх коефіцієнтів моделі одночасно. Значущість F – це теоретична імовірність того, що при виконанні цієї гіпотези F-статистика більше емпіричного значення F. За допомогою критерію адекватності Фішера F перевіряється існування зв’язку між результуючою та незалежними змінними. Рівняння регресії значуще на рівні α, якщо F > F_t, де F_t – табличне значення F-критерію Фішера.

За F-таблицями Фішера знаходиться критичне значення F_t з m та (n-m-1) ступенями вільності, задавши попередньо рівні значущості .

Як свідчить проведене дослідження, модель є статистично значущою, а гіпотеза про наявність зв’язку між залежною та незалежними змінними підтверджується, оскільки значення розрахункового критерію F_t більше значення критерію F.

Результати регресійного аналізу

Y-пересечение – вільний член рівняння регресії; X1 – член регресійної моделі. Кількість рядків відповідає кількості функцій у моделі регресії; Коэффициенты – коефіцієнти при відповідних членах регресійного рівняння; Стандартная ошибка – середньоквадратична похибка при визначенні значення відповідного коефіцієнта регресійного рівняння; t-статистика – t-статистика, показує значущість даного коефіцієнту; P-значение – імовірність можливості хибного висновку на основі одержаних даних; P-значення також визначає ймовірність, що дозволяє визначити значущість коефіцієнтів регресії. Порівнюємо P-значення з рівнем значущості α= 0.05. Отже, коефіцієнти моделі значущі, оскільки всі значення стовпчику «P-значение» менші за α= 0,05. Якщо Р < 0,05, то оцінки параметрів достовірні.

Нижние 95 %, Верхние 95 % – межі довірчого інтервалу для значення коефіцієнту (параметру моделі) при рівні достовірності 95 %.

Таким чином, рівняння множинної регресії має вигляд:

Y= 9,65 X1 – 0,31X2 – 27,99 ,

де Y – заробітна плата; Х₁ – рентабельність; Х₂ – затрати капіталу.

Таким чином, за допомогою пакета регресійного аналізу в MS Excel була побудована багатофакторна лінійна регресійна модель, що відображає залежність розміру заробітної плати від рентабельності виробництва та затрат капіталу. Відповідно до проведеного дослідження отриманої моделі її якість є високою, оскільки коефіцієнт множинної кореляції R свідчить про тісний зв’язок усіх незалежних перемінних і результуючої перемінної; коефіцієнт детермінації моделі R² показує високу адекватність моделі, що підтверджує і скоректований коефіцієнт детермінації; а критерій адекватності Фішера F характеризує високу статистичну значущість отриманої моделі.