Скалярное произведение векторов и его свойства.

1. Определение.

.

2. Основные свойства.

1. Коммутативность (переместительное свойство):

;

2. Ассоциативность (сочетательное свойство):

;

3. Положительная (неотрицательная) определенность:

, причем ;

4. Дистрибутивность (распределительное свойство):

.

3. Частные значения

1. , если и ;

2. - острый угол;

3. - тупой угол;

4. или .

4. Скалярное произведение в декартовой системе координат

Координаты вектора

.

Скалярное произведение

.

Длина вектора

.

Расстояние между точками

.

Угол между векторами

.

Направляющие косинусы

.

Проекция одного вектора на другой

.

Основные свойства векторного произведения

1. Антикоммутативность (переместительное свойство):

;

2. Ассоциативность (сочетательное свойство):

;

3. Дистрибутивность (распределительное свойство):

.

4. Параллельность векторов и векторное произведение

.

5. Площадь параллелограмма и модуль векторного произведения

.

Векторное произведение в декартовом базисе

,

.

Запись с помощью тензора Леви-Чивита.

.

Запись с использованием определителей второго порядка:

,

.

Запись с помощью определителя третьего порядка:

.

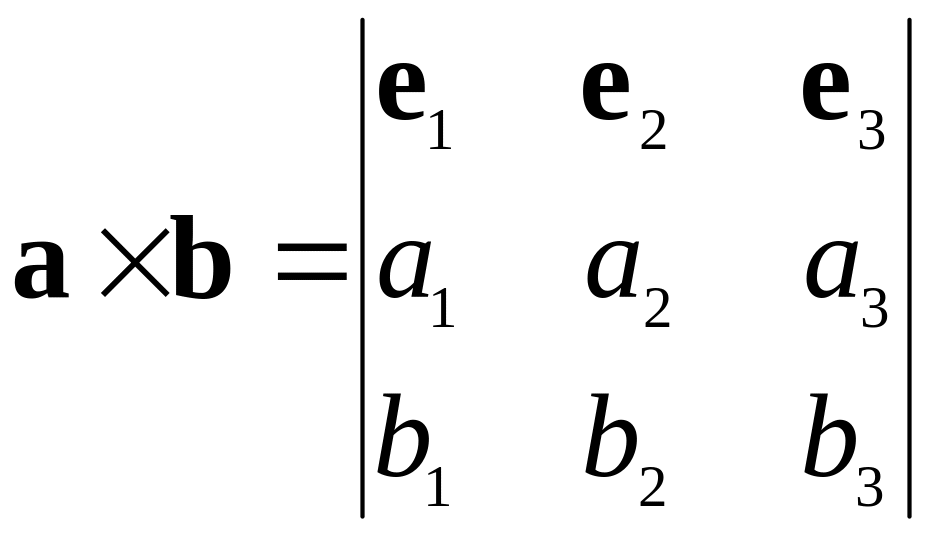Основное свойство смешанного произведения. Смешанное произведение трех векторов , , равно ориентированному объему параллелепипеда, построенного на векторах , , , как на сторонах:

Другие свойства.

1. Смешанное произведение компланарных векторов равняется нулю:

2. .

3. В смешанном произведении знаки умножения можно менять местами.

4. Ориентация и смешанное произведение

– правая тройка векторов;

– левая тройка векторов.

5. Распределительный закон смешанного произведения

.

6. Смешанное произведение в декартовом базисе.

.

Правило раскрытия двойного векторного произведения:

= .

Двойное векторное произведение равно разности произведения среднего вектора на скалярное произведение остальных векторов и произведения другого вектора в скобках на скалярное произведение остальных векторов.

Прямое и обратное преобразование декартовых координат при поыороте и параллельном переносе.

и .

Уравнения прямой линии на плоскости.

N	Название	Уравнение
1	Общее уравнение
2	Нормальное
3	В отрезках
4	С угловым коэффициентом
5	Каноническое
6	Через две точки
7	Параметрическое в координатах
8	Параметрическое через две точки
9	Векторное параметрическое
10	Векторное параметрическое через две точки
11	Векторное

Нормаль к прямой

.

Возможные выражения для направляющего вектора:

, и т.п.

Отрезки, отсекаемые на осях:

, .

Угловой коэффициент:

.

Абсолютное значение величины

определяет расстояние от точки до прямой, а ее знак – их взаимное расположение.

Уравнения плоскости

N	Название уравнения	Уравнение
1	Общее уравнение
2	Нормальное
3	В отрезках
4	Векторное параметрическое, заданное а)одной точкой и двумя направляющими векторами, б) тремя точками, в) двумя точками и одним направляющим вектором.	; ; .
5	Параметрическое, заданное а) точкой и двумя направляющими векторами, б) тремя точками, в) двумя точками и одним направляющим вектором.	;
6	Векторное, заданное нормалью
7	Векторное, заданное а) направляющими векторами, б) двумя точками и одним направляющим вектором, в) тремя точками.	, , .
8	Векторное уравнение плоскости в координатной записи, заданное а) направляющими векторами, б) двумя точками и одним направляющим вектором, в) тремя точками.	, ,

Нормаль к плоскости

.

Выражение нормального вектора через направляющие

.

Отрезки, отсекаемые на осях:

, , .

Абсолютное значение величины

определяет расстояние от точки до прямой, а ее знак – их взаимное расположение.

Таблица 12.2. Уравнения прямой линии в пространстве.

N	Название уравнения	Уравнение
1	Векторное параметрическое
2	Векторное параметрическое заданное двумя точками.
3	Параметрическое в координатах
4	Параметрическое, заданное двумя точками
5	Каноническое
6	Через две точки
7	Общее уравнение
8	Векторное
9	Векторное, заданное двумя точками

Если прямая задана, как пересечение двух плоскостей, то ее направляющий вектор определяется нормальными к этим плоскостям векторами:

.

Краткие сведения о линиях и поверхностях.

1. Уравнение линии на плоскости

.

2. Уравнение поверхности в пространстве .

.

3. Уравнение линии в пространстве .

.

4.Параметрическое уравнение линии

.

5. Параметрическое уравнение поверхности

.

6. Уравнение цилиндра

.

7. Уравнение конуса

, если .

8. Уравнение поверхности вращения

.

Классификация линий второго порядка.

N			Тип			Название линии	Уравнение
1	Центральные I2 ≠ 0		Эллиптический			Эллипс
2						Точка (пара мнимых пересекающихся прямых)
3						Мнимый эллипс
4			Гиперболический			Гипербола
5						Пара пересекающихся прямых
6	Нецентральные		Параболический			Парабола
7				I3=0	K<0	Пара параллельных прямых
8					K=0	Пара совпадающих прямых
9					K>0	Пара параллельных мнимых прямых

Алгоритм определения вида линии второго порядка с помощью инвариантов

Определение параметров линии второго порядка.

.

1. Эллипсы и гипербола.

Координаты центра:

Корни характеристического уравнения:

Дискриминант

Угол поворота ( ): , ,

, .

Вещественный и мнимый эллипс: .

Полуоси:

Гипербола: .

Полуоси: , где .

2. Пересекающиеся прямые (диагонали основного прямоугольника).

или .

3. Параллельные прямые

или .

4.Парабола.

Параметр:

Угол поворота:

; .

Ось параболы

, или .

Вершина определяется как точка пересечения параболы с ее осью.

5. Оси координат канонической системы отсчета

Ось абсцисс: .

Ось ординат:

У параллельных прямых определена только ось абсцисс одним из уравнений:

или .

Краткие сведения о поверхностях второго порядка.

Вещественный эллипсоид	Мнимый эллипсоид
Однополостный гиперболоид	Двуполостный гиперболоид
Эллиптический параболоид	Гиперболический параболоид
Вещественный конус	Мнимый конус (точка)
Девять цилиндров, соответствующих девяти линиям второго порядка.

20