2. 1. Общие сведения об уравнениях и их решении

Решение многих научных и технических задач сводится к составлению и решению уравнений. Следовательно, специалист в любой отрасли техники должен уметь решать любые уравнения как обычными средствами вычислений, так и с помощью компьютера.

Обычно уравнения имеют вид f (x)=0, где f-заданная функция.

Уравнения называются нелинейными , если линия , построенная по заданной функции, не является прямой. Нелинейные уравнения делятся на два класса : алгебраические и трансцендентные. Алгебраическими называют уравнения, если заданная функция является полиномом n - ой степени . Нелинейные уравнения, содержащие тригонометрические, логарифмические и другие элементарные функции называются трансцендентными .

Поиски методов решения нелинейных уравнений начались с попыток вывода формул, аналогичных формуле для решения квадратного уравнения , которая выражает значения корней уравнения через его коэффициенты . Для алгебраических уравнений третьей и четвертой степени такие формулы были получены. Однако практическое значение этих формул невелико, так как их применение приводит к дополнительным и довольно сложным вычислениям. Покажем это на примере решения кубического уравнения .

Пусть дано кубическое уравнение у ³ + а у ² + в у + с = 0. Заменяя в уравнении неизвестное у новым неизвестным x, связанным с у равенством у= x- а /3, получают уравнение относительно неизвестного x, не содержащее квадрата этого неизвестного, т.е. уравнение вида:

x + p x + q = 0 (1) .

Если будут найдены корни уравнения ( 1 ) ,то можно получить и корни заданного уравнения благодаря равенству у = x - а / 3 . Следовательно, необходимо уметь решать « неполное» кубичное уравнение . Формулы, выражающие корни уравнения (1) через его коэффициенты при помощи квадратных и кубичных радикалов , были получены итальянским математиком Кардано в ХV I веке . Формулы Кардано имеют следующий вид :

X= + (2)

Так как кубичный радикал имеет в поле комплексных чисел три значения, то формула (2) дает по три значения для каждого радикала, входящего в формулу (2). Однако, применяя формулу Кардано, нельзя комбинировать любое значение первого радикала с любым значением второго. Для данного значения первого радикала  следует брать лишь то из значений второго радикала  , которое удовлетворяет условию   = - p /3 .

В курсе высшей алгебры доказано, что при определенных соотношениях коэффициентов p и q в уравнении (1), все три корня этого уравнения являются действительными числами. Однако разыскание их по формуле Кардано требует извлечения кубичных корней из комплексных чисел, что возможно сделать лишь путем перехода к тригонометрической форме этих чисел. Поэтому запись корней кубичного уравнения с помощью радикалов не имеет практического значения .

Аналогично обстоит дело и с решением алгебраических уравнений четвертой степени. Формулы, выражающие корни уравнения через его коэффициенты, были получены итальянским математиком Феррари еще в ХVI столетии, однако в практических расчетах никто ими не пользуется в связи с их громозкостью и сложностью вычислений.

После Феррари почти три столетия продолжались безуспешные попытки сделать следующий шаг, т.е. найти формулы, выражающие корни уравнения пятой степени через его коэффициенты. Эти попытки прекратились лишь после того, как норвежский математик Абель в двадцатых годах XIX столетия доказал, что такие формулы для уравнений n - ой степени при любом n 5 заведомо не могут быть найдены.

Это обстоятельство послужило толчком для многочисленных исследований, имевших целью получение методов приближенного вычисления корней. Такой подход оправдан еще и тем, что при решении технических проблем обычно достаточно знать лишь приближенные значения корней с заранее заданной точностью. Если бы корни многочлена и можно было бы записать в радикалах, то эти радикалы все равно были бы заменены их приближенными значениями. Кроме того, уравнение может содержать коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнений теряет смысл. Все указанные причины привели к появлению так называемых итера-ционных методов решения нелинейных уравнений. С их помощью решение уравнения достигается путем многократного применения некоторого алгоритма, который позволяет вычислить приближенные значения корней уравнения с заранее заданной точностью. Обычно это делается в два этапа:

1). о т д е л е н и е к о р н е й, т.е. установление возможно тесных промежутков  , , в которых содержится один корень уравнения ;

2). у т о ч н е н и е п р и б л и ж е н н ы х к о р н е й , т.е. доведение их до заданной степени точности.

Д а л е е р а с с м о т р е н к а ж д ы й и з э т а п о в .

2. 2. О т д е л е н и е к о р н е й

Пусть дано уравнение f(x)=0, в котором функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале а<x<в. Всякое значение  , обращающее функцию f(x) в нуль, т.е. такое, что f()=0, называется корнем уравнения. Для отделения корней полезна известная из математического анализа теорема Больцано-Коши :

Если непрерывная функция f(x) принимает значения разных знаков на концах отрезка (  ,) ,т.е. если f() f() <0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x)=0,т.е. найдется хотя бы одно число   (,) такое, что f()=0.

Процесс отделения корней начинается с установления знаков функции f(x) в граничных точках области существования функции. Затем определяются знаки функции f(x) в ряде промежуточных точек x=  ₁ , ₂ , ...  , выбор которых учитывает особенности функции f(x). Если окажется, что

f( _к ) f(  _к+1 )<0, то в силу теоремы Больцано-Коши в интервале ( _к , _к+1) имеется корень уравнения f(x)=0 .

Если функция f(x) является многочленом n -ой степени, то эта функция определена в бесконечном интервале -  < x<+ . Для определения промежутка, в котором находится хотя бы один корень уравнения, придется вычислять значение функции f(x) в большом количестве промежуточных точек. Для сужения интервала, в котором следует проводить поиск корней алгебраических уравнений, можно воспользоваться следующей теоремой из высшей алгебры: для многочлена f(x) c любыми числовыми коэффициентами число C=1+Am/ (*) служит верхней границей для модулей всех его корней, включая комплексные, где - модуль коэффициента при x , Am - максимальный модуль из остальных коэффициентов.

П р и м е р 1 . Найти интервал , внутри которого находятся корни многочлена f(x)= x + 2 x - 5 x +8 x - 7 x - 3

Для этого многочлена =1, Am =8. Отсюда С=1+8/1=9 ,таким образом, все пять корней многочлена находятся внутри интервала  -9, +9  .

Интервал, определяемый с помощью формулы (*) , оказывается слишком большим, особенно для действительных корней. Чтобы уменьшить объем вычислений , были разработаны более точные, но и более сложные методы определения границ интервалов, содержащих действительные корни. Если вычисления проводить с помощью компьютера, то их объем большого значения не имеет, и потому нет необходимости рассматривать здесь иные методы определения границ интервалов.

П р и м е р 2. Отделить действительные корни многочлена, рассмотренного в примере 1: f ( x )= х⁵ + 2 x⁴ - 5 x³ + 8 х² - 7 x - 3 .

Для решения этой задачи вычисляются значения полинома, приняв за начальное значение x = - 9 и шаг изменения аргумента  x = 1 . Результаты вычислений приведены в таблице 2 .

Т А Б Л И Ц А 2

X	- 9	- 8	- 7	- 6	- 5	- 4	- 3	- 2
У	-39574	-21451	-9852	- 1377	-1018	- 39	+ 144	+ 83

П р о д о л ж е н и е т а б л и ц ы 2

Х	- 1	0	+ 1	+ 2	+ 3	+ 4	+ 5	+ 6
У	18	-3	- 4	39	480

Из таблицы видно, что многочлен f(x) имеет по крайней мере три действительных корня : положительный 1 < x < 2 , так как f (1) <0 , а f(2) >0 , и два отрицательных - 1 < x < 0

( f ( - 1 ) = + 18 , f ( 0 ) = - 3 ) , - 4 < x ₃ < -3 ( f ( - 4 ) = - 39, f ( -3 ) = + 144) .

Трансцендентные уравнения чрезвычайно разнообразны, поэтому отделение корней в них несколько сложнее. Для проведения этой операции приходится анализировать функцию f(x) и во многих случаях строить ее график, чтобы определять приближенно точки пересечения этого графика с осью абсцис. Часто бывает выгодно первоначальное уравнение f(x) = 0 заменять равносильным ему уравнением  (x) =  (x), где функции  (x ) и  (x) - более простые, чем функция f(x ). Тогда, построив графики функций у =  (x) и у =  (x), искомые корни получают как абсциссы точек пересечения этих графиков.

П р и м е р 3 . Найти приближенное значение корня уравнения

x lg x - 1 = 0 . ( 3 )

Полагая x  0 , разделим уравнение на x и запишем его в следующим виде : lg x= 1 / х. Отсюда видно, что  (x) = lg x, а  (x) = 1 / x, где

 ( x ) - логарифмическая кривая , а  (x) - гипербола. Решением уравнения ( 3 ) является абсцисса точки пересечения логарифмической кривой и гиперболы. Поскольку логарифмическая кривая при x < 0 не существует, то точку пересечения кривых  ( x ) и  ( x ) следует искать при x 0 .

Для построения кривой необходимо, как минимум, три точки. Найдем их для каждой кривой. За начальное значение x примем х=1 , шаг изменения x для простоты вычислений принимается равным также единице. Вычисления приведены в табличной форме.

Та б л и ц а 3

X	1	2	3
lg x	0	0 ,30	0 , 48
1 / x	1	0, 50	0 ,33
Lgx-1/x	-1	- 0, 20	+0 , 15

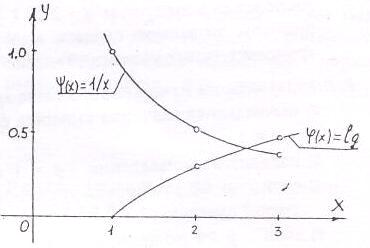
Из таблицы 3 и рисунка видно , что корень уравнения ( 3 ) находится в интервале ( 2 ; 3 ) .

П р и м е р 4 . Найти приближенное значение корня уравнения

e - x - 2 = 0 ( 4 )

Перенося последние два члена уравнения в правую часть , получаем эквивалентное уравнение e = x + 2 . Из этого равенства видно , что корнем уравнения является абсцисса точки пересечения графика показательной функции  ( x ) = e и прямой линии  (x) = x + 2 .

График показательной функции располагается над осью x при любых значениях x - положительных и отрицательных . Прямая же  (x) = x+ 2 располагается над осью x только при x>-2. При этих значениях x и следует искать точки пересечения графиков функций  (x) и (x).За начальное значение аргумента обоих функций принимается x = -2 . Шаг изменения x принимается равным единице .Вычисления значений функций (x) , (x) и заданной функции f(x)=e -х-2 проводятся в табличной форме .

Та б л и ц а 4

X	-2	- 1	0	+ 1	+ 2
e	0,135	0 , 368	1	2 ,72	7 ,39
X + 2	0	1	2	3	4
f (x)	0 ,135	- 0, 632	- 1	- 0 ,28	+3 ,39

Из таблицы 4 видно, что графики функций  (x) и  (x) пересекаются в двух точках . Следовательно , уравнение ( 4 ) имеет два корня один из них расположен в интервале ( - 2 ; - 1 ) , второй- в интервале (1;2) . Рассмотренные примеры позволяют сделать вывод ,что отделение корней алгебраических и трансцендентных уравнений можно проводить по единому алгоритму :

1. назначается начальное значение аргумента x и шаг его изменения  x;

2. вычисляются значения заданной функции f(x)в точках x = x и

x = x + x ;

3. находится произведение p = f(x ₁ )  f(x ₂ ) ;

4. если p <0 , то корень уравнения находится внутри интервала ( x ; x ), расчет окончен ;

5. если p >0 ,то принимается x = x + x , x = x +x = x + 2  x , и все действия начиная с п. 2 , повторяются .

Разница для алгебраических и трансцендентных уравнений заключается в том, что для алгебраических уравнений значение x может быть вычислено по формуле ( * ) , а для трансцендентных уравнений значение х_о должно быть получено путем анализа заданной функции f (x).

Рассмотренный алгоритм может быть реализован в виде подпрограммы на языке Ф О Р Т Р А Н . Как известно , в Ф О Р Т Р А Н е применяются подпрограммы двух видов : F U N C T I O N и S U B R O U T I N E . Подпрограмма F U N C T I O N употребляется в тех случаях, когда необходимо вычислять и передавать в вызывающую программную единицу единственное значение . В других случаях - S U B R O U T I N E .

В нашем случае подпрограмма должна выдать значения границ интервала, внутри которого содержится корень уравнения , и количество шагов , совершенных на пути к этому интервалу .Т.е. здесь может быть применена только подпрограмма типа S U B R O U T I N E . При «ручном » счете подсчет количества шагов не обязателен , но при расчете на компьютере он необходим .Дело в том , что при неудачном задании начального значения аргумента компьютер будет совершать шаг за шагом , не находя интервала , содержащего корень уравнения . И выйти из цикла , повторяющего п.п. 2 - 5 описанного выше алгоритма , самостоятельно он не сможет . В этом случае говорят , что «компьютер зациклился » . Чтобы не произошло зацикливания, количество шагов должно быть ограничено некоторым достаточно большим числом , по достижении которого компьютер должен прекратить вычисления, выдав сообщение, что за оговоренное количество шагов интервал , содержащий корень уравнения , не найден . В этом случае оператор должен задать новое значение x и снова запустить программу .

В подпрограмме должны неоднократно вычисляться значения функции

f(x) .Чтобы подпрограмму не приспосабливать к каждому решаемому уравнению , вычисления функции f (x) должны проводиться путем вызова подпрограммы - функции F U N C T I O N F ( x ). И только эта подпрограмма должна быть написана заново для каждого решаемого уравнения. С учетом изложенного подпрограмма отделения корней нелинейных уравнений может иметь, например, вид, приведенный в приложении 1 .

2. 3. Р е ш е н и е н е л и н е й н ы х у р а в н е н и й м е т о д о м

п о л о в и н н о г о д е л е н и я .

Пусть дано уравнение f (x)= 0 , ( 1 ) ,

один из корней которого отделен , т.е. найден отрезок ( а , в ) , на концах которого значения функции f(x) имеют разные знаки . Для нахождения корня уравнения отрезок ( а, в ) делится пополам и вычисляется значение функции f (x) в точке  = ( а + в ) / 2 . Если f (  ) = 0 , то  является корнем уравнения. Обычно в технических задачах можно удовлетвориться приближенным значением корня . Поэтому корнем уравнения можно считать и то значение , при котором f(  )   , где  - заранее назначенная малая величина , определяющая точность решения уравнения .

Если f(  )> , то рассматривается та половина отрезка ( а ,  ) или

(  , в ) , на концах которой функция f (x) имеет разные знаки. Т.е. получают суженный отрезок ( а , в ) , где а = а в =  , или а =  , в = в . Отрезок ( а , в ) снова делится пополам и проводится то же рассмотрение , что и для первоначального отрезка . В результате на каком -то этапе получают или корень уравнения ( 1 ) , или последовательность вложенных друг в друга отрезков ( а , в ) , ( а , в ) , . . ( а , в ) ,таких ,что f(a ) f ( в ) < 0 и в - а = ( в - а ) / 2 (2)

Из формулы (2) видно ,что после n итераций (приближений ) разность в - а может быть очень малой . Если ( в - а )  2  , то координата середины отрезка и есть значение корня с требуемой точностью  .

Метод половинного деления ( метод бисекций ) - простой и надежный метод поиска корня уравнения f ( x )= 0 . Он сходится для любых непрерывных функций . Скорость его сходимости невелика. Однако алго-ритм этого метода прост и легко реализуется на компьютерах.

На основе разобранного выше алгоритма составлена подпрограмма типа S U B R O U T I N E с именем D E L P O . Входными параметрами этой подпрограммы являются границы отрезка (а,в). Подпрограмма D E L P O выдает значение корня уравнения, значение функции f(x), и количество итераций, сделанных для достижения заданной точности корня. Величина  , определяющая точность решения уравнения, вводится с клавиатуры . Ре-шаемое уравнение содержится во внешней функции F (x) , подпрограммы D E L P O . Текст подпрограммы представлен в приложении 2.

Исходные данные и результаты расчетов выводятся на экран дисплея и записываются в стандартный файл f t 0 7 f 0 0 1 на диск с помощью специиальной подпрограммы I D R E S, текст которой представлен в приложении 2 .

Таким образом , решение нелинейных уравнений методом бисекций можно свести к составлению главной программы, вызывающей три опи-санные выше подпрограммы , и составлению подпрограммы вычисления функции F ( x ). Образец главной программы приведен в приложении 2 .

2. 4. Р е ш е н и е н е л и н е й н ы х у р а в н е н и й м е т о д о м х о р д

Метод хорд является более быстрым способом нахождения корня уравнения f (x)=0 , нежели метод половинного деления (Рис. 1).

Пусть функция f(x) непрерывна на отрезке ( а , в ) и f ( а ) f ( в ) < 0.

Для определения корня в первом приближении проведем прямую через две точки ( а , f (а) ) и ( в , f (в) ) и найдем точку пересечения x этой прямой с осью абсцисс . Если f(x )   , где  - малое число , опреде-ляющее точность решения уравнения, то х принимается за корень уравнения

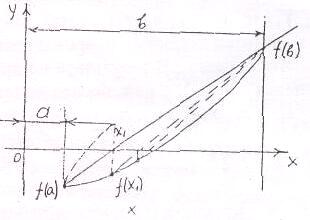
Рис. 1

Если f(x )   , то находится произведение f(a) f (x ). Если f (а) f (x )0 , то за неподвижный конец хорд принимается точка ( в, f(в)), если f(а) f(x ) < 0 , то - точка ( а , f( а )). Снова проведем хорду, которая пересечет ось

абсцисс ближе к точке пересечения кривой f(x) с осью x. При f (а) f(x )  0 хорда проводится через точки ( x , f(x ) , (в, f( в ) ) , т . е . роль точки а играет точка ( x , f(x )) . Чтобы получить координаты точки пересечения новой хорды с осью x достаточно в первоначальном уравнении хорды « а » заменить на x , а f(а) - на f(x ) . Аналогично обстоит дело и в случае f(а) f(x ) <0.

Теперь получим аналитическое выражение изложенных выше словесных рассуждений . Уравнение прямой , проходящей через заданные две точки , имеет вид

=

Разрешим это уравнение относительно x:

x -x = (y -y )

Учитывая, что в точке пересечения хорды с осью x у=0 , получаем:

x= x - y (x - x ) / (y - y )

По условию у =f(а); у = f(в), x = а; x = в.

С учетом этого получаем:

x= а - f(а ) ( в - а ) / ( f(в ) - f( а) ) ( 1 )

По этой формуле вычисляется значение корня уравнения в первом приближении. Проверяем точность вычисленного корня. Если  , то вычисления прекращаются. Если f(x)  , то вычисляется произведение f(а) f(x) . Если f(а) f(x)  0 , то принимается а = x f(а) = f(x) и по этим данным по формуле ( 1 ) вычисляется новое значение х. Если же f(a) f(x)<0 , то принимается в =x, f(в)=f(x) и по этим данным вычисляется новое значение х. Так продолжается до тех пор, пока не будет выполняться неравенство f (x)  , или пока два последовательных значения x не будут отличаться не более, чем на  , т.е.  ₁ . На основе этого алгоритма составлена подпрограмма H O R D , текст которой приведен в приложении 3 .

Пример решения уравнения методом хорд приведен также в приложении 3 .

2. 5. Р е ш е н и е н е л и н е й н ы х у р а в н е н и й м е т о д о м

к а с а т е л ь н ы х

Метод касательных , называемый также методом Ньютона, широко используется при построении итерационных алгоритмов. Его попу-лярность объясняется быстрой сходимостью при хорошем начальном приближении . Метод Ньютона основан на замене небольшой дуги кривой у=f(х) касательной , проведенной в некоторой точке этой кривой (Рис. 2) .

Зададимся некоторой точкой х_о ,у_о , лежащей на кривой у=f(х) , и найдем уравнение касательной к этой кривой в выбранной точке. Касательная имеет наклон к оси абсцисс , обусловленный видом кривой f(х), т.е. при проведении касательной , кроме координат точки , должен быть выдержан и угол наклона кривой в выбранной точке. Таким образом, уравнение касательной - это уравнение прямой , проходящей через заданную точку с заданным угловым коэффициентом . Общий вид такого уравнения известен из курса аналитической геометрии :

у – у_о = к ( х – х_о) , ( 1 )

где к- угловой коэффициент, т.е. тангенс угла между прямой и осью х.

Найдем точку пересечения этой прямой с осью абсцисс . Для точки , лежащей на оси х , у = 0 . Подставляя это значение у в ( 1 ) , получаем

- у_о = кх - кх_о ; кх_о - у_о = кх ; х = х_о - у_о / к . ( 2 )

Поскольку точка ( х_о , у_о ) лежит на кривой у = f (х) , то у_о = f (х_о) , а

к = tg = dy / dx = f ‘(x _o) . Подставляя найденные значения у_о и к в формулу ( 2 ) , получаем :

х = х_о - f’(х_о) / f (х_о) ( 3 )

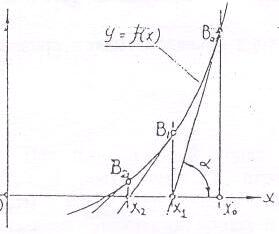
Рис. 2

Для выбора начального приближения в методе Ньютона необходимо проверить выполнения условия:

f (с) / (с) > 0, с = b или с = а. (4)

касательная к точке C проводится со стороны выпуклости функции. За начальное приближение итерационного процесса выбирается тот из конца отрезка (а, b) в котором выполняется условие (4).

Найденное значение х считаем значением корня уравнения у = f (х) в первом приближении , т.е. х₁ = х₀ – f(х_о) / f’ (х_о ). Для получения корня во втором приближении надо найти значение функции f ( х₁) , провести каса-

тельную к кривой f (х) в точке В₁ ( х₁ , у₁ ) и найти точку пересечения новой касательной с осью х . Абсцисса этой точки найдется по формуле

х₂ = х₁ - f(х₁) /f’ (х₁)

Обобщая эту формулу , можно для любого приближения записать

х_n+1 = x_n – f(x_n) / f‘(x_n) . ( 4 )

Процесс вычислений по формуле (4) прекращается , если два после-довательных значения х близки, т.е. если х_n+1 – х_n  , где  - малое число, определяющее требуемую точность решения уравнения . Процесс вычислений может быть прекращен и в том случае , если f(х_n+1) ₁ .

Скорость сходимости процесса последовательных приближений по методу Ньютона в большой мере зависит от удачного выбора исходной точки . Если численное значение производной f' (х) вблизи кор-ня мало, то процесс вычисления корня может оказаться длительным . Если же в окрестности корня график функции имеет большую крутизну, то процесс быстро сходится. Следовательно, если определен отрезок , внутри которого находится корень уравнения, то в качестве начального приближения корня следует принять тот конец отрезка , на котором модуль первой производнойf' (х) имеет большее значение .

Из всего сказанного следует , что для решения уравнений методом Ньютона необходимо иметь : уравнение функции f(х) , уравнение производной f' (х) , начальное приближение корня уравнения х_о , значение малой величины  , определяющей момент выхода из итерационного процесса , счетчик итераций , позволяющий автоматически прервать расчет , если количество итераций превысит заданное значение . Алгоритм решения уравнения может быть представлен в следующем виде :

1) выбрать начальное значение корня х_n ;

2) по формуле ( 4 ) вычислить х_n+1 ;

3) если х_n+1 - x_n  , то перейти к п. 7;

4. 4) вычислить f (x_n+1 ) ;

5) если f (x_n+1 )  , то перейти к п. 7 ;

4. 6) положить х_n = x_n+1 и перейти к п. 2 ;

5. 7) закончить расчет .

Этот алгоритм реализован в виде подпрограммы SUBROUTINE NEWTO ( A, B, EPS, X, K ).Текст подпрограммы приведен в приложении 4 .

2. 6. Р е ш е н и е н е л и н е й н ы х у р а в н е н и й м е т о д о м

п р о с т ы х и т е р а ц и й

Этот метод решения уравнения f(х) = 0 состоит в замене исходного уравнения эквивалентным ему уравнением х = (х) и построении последовательности х_n+1 =  (х_n) , сходящейся к точному решению при n . Достаточным условием сходимости является выполнение неравенства ¹х 1 на отрезке (а, в) . Поэтому прежде чем проводить вычисления корня, необходимо проверить выполнение условия сходимости вычислением значения ¹ (х) на концах отрезка (а , в) . Если ¹а и  ¹(в) , то можно начинать вычисления корня уравнения .

Может оказаться, что функция  (х) такова , что ее первая производная всегда > 1 по модулю.

В таком случае следует поискать такое преобразование функции (х) , чтобы у преобразованной функции ₁(х) выполнялось условие

₁¹ (х) . Если такое преобразование найти не удалось, то уравнение следует решать каким – либо другим методом .

Пример . Установить можно ли решить уравнение е^х – х – 2 = 0 методом простых итераций.

В п. 2.2. (пример 4) было установлено , что один из корней рассматриваемого уравнения находится на отрезке ( 1; 2 ) . Преобразовываем исходное уравнение к виду , удобному для решения методом простых итераций : х = е^х – 2 . В этом уравнении (х) = е^х – 2 . Находим первую производную функции  (х) : ¹ (х) = е^х . При х > 0 е^х >1 , следовательно , уравнение х = е^х - 2 методом простых итераций решить нельзя. Значит, первоначальное уравнение надо преобразовать к другому виду .

Запишем первоначальное уравнение в следующем виде е^х= х + 2 . Логарифмируя правую и левую части , получаем х = ln(х+2) . Теперь  (х) = ln(х+2) , ¹(х) = 1 / (х+2) . При х > 0 ¹ (х)  , т.е. теперь процесс итераций будет сходящимся , и уравнение можно решать методом простых итераций.

Когда сходимость процесса установлена , задаются начальным значением корня х_о и вычисляют первое приближение корня х₁=  (х_о) . Если х₁ – х_о  , то выполняют очередную итерацию х₂ =  (х₁) и т. д. Если после выполнения n итераций окажется , что х_n+1- х_n  , то вычисления заканчивают и за приближенное значение корня уравнения f(х) = 0 принимают величину х_n+1 . Из цикла вычисления корня уравнения можно выйти и в том случае , если значение первоначальной функции f(х) будет мало отличаться от нуля , т.е. если f (x_n+1) .

Из сказанного выше видно , что для решения уравнений методом простых итераций необходимо иметь: первоначальное уравнение f(х) = 0 , эквивалентное уравнение х =  (х) , выражение первой призводной эквивалентного уравнения ¹(х) , начальное приближение корня х_о и значение малой величины  , определяющей момент выхода из итерационного процесса .

Если отрезок ( а , в ) , содержащий корень уравнения f (х) = 0 , определен , то алгоритм решения уравнения может быть представлен в следующем виде :

1) вычислить значения ¹(х) на концах отрезка ( а , в ) ;

2) если ¹(а) или ¹(в)  , то перейти к п. 9 ;

3) выбрать начальное значение корня а  х_n  в ;

4) вычислить х_n+1 =  (х_n)

5) если х_n+1 – х_n  , то перейти к п. 9 ;

6) вычислить f (х_n+1) ;

7) если f (x_n+1)  , то перейти к п. 9 ;

8) положить х_n = х_n+1 и перейти к п. 4 ;

9) закончить расчет.

Этот алгоритм реализован в виде подпрограммы SUBROUTINE PRITE ( A, B, EPS, X, K ) .

Текст этой подпрограммы и пример решения уравнения методом простых итераций приведен в приложении 5.

Метод допускает простую геометрическую интерпретацию. Построим графики функций у = х и у =  (х). Корнем ξ уравнения х =  (х) является абсцисса точки пересечения кривой у =  (х) с прямой у = х (рис. 3). Взяв в качестве начальной произвольную точку х₀ ε [a, b], строим ломанную линию (рис. 3, а, б). Абсциссы вершин этой ломанной представляет собой последовательные приближения корня ξ.

Рис. 3