6. Смешанное произведение трех векторов
О п р е д е л е н и е
10. Смешанным
произведением
трех векторов
,
и
называется число, обозначаемое
,
равное скалярному произведению векторов
и
,
то есть
.
Свойства смешанного произведения:
1)
;
Абсолютная величина смешанного произведения трех векторов численно равна объему параллелепипеда, построенного на этих векторах (рис. 6):
ç
ç.
Рис. 6
3) Объем тетраэдра (пирамиды, в основании которой лежит треугольник, рис. 7), построенного на векторах , и , численно равен:
ç
ç.
Рис. 7
4) Три вектора , и компланарны (параллельны одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю:
,
,
-
компланарны
=0.
5) Если известны координаты векторов
,
и
,
то их смешанное произведение вычисляется по формуле:
(7)
7. Примеры с решениями
П р и м е р 1. Даны точки
и
Найти векторы
Р е ш е н и е. Найдем
векторы
:
1)
Следовательно,
2)
.
Следовательно,
Найдем вектор
:
Иначе это действие можно оформить так:
Аналогично:
,
откуда
Теперь найдем вектор
:
Иначе это действие можно оформить так:
О т в е т:
.
П р и м е р 2. Даны точки
,
.
Показать, что четырехугольник ABCD является трапецией.
Р е ш е н и е. Известно, что у трапеции две противолежащие стороны параллельны (основания трапеции), а две другие – нет.
Для решения данной задачи достаточно убедиться в коллинеарности двух векторов, лежащих на противоположных сторонах четырехугольника ABCD, то есть мы должны показать, что
или
.
Найдем эти векторы и рассмотрим отношения их соответствующих координат, поскольку известно, что у коллинеарных векторов координаты пропорциональны.
В данном случае
Нетрудно видеть, что , так как
,
Векторы
и
не являются коллинеарными, поскольку
их соответствующие координаты не
пропорциональны:
Следовательно, ABCD трапеция, так как
, .
О т в е т: ABCD трапеция.
П р и м е р 3.
Даны векторы
и
Найти их скалярное произведение.
Р е ш е н и е. Воспользуемся формулой (3):
О т в е т:
П р и м е р 4.
Угол между векторами
и
равен
.
Известны длины векторов:
=4;
=5.
Найти длину вектора
Р е ш е н и е. Воспользуемся тем, что длина вектора равна квадратному корню из скалярного квадрата этого вектора:
=
О т в е т: =7.
П р и м е р 5. Даны векторы
и
Найти длину их векторного произведения.
Р е ш е н и е. Поскольку векторы заданы координатами, найдем их векторное произведение по формуле (6):
=
.
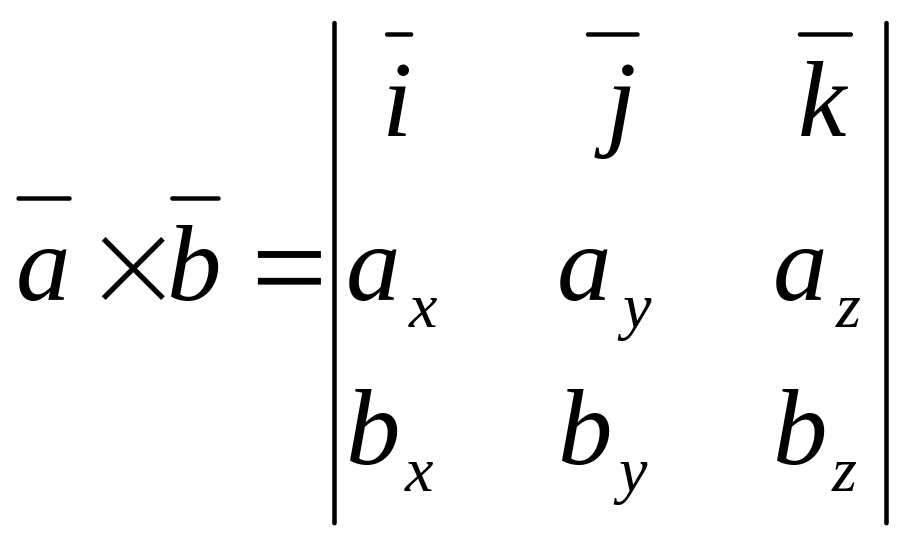Найдем теперь длину полученного вектора:
ç
ç=
.
О т в е т:
.
П р и м е р 6. Даны точки А(2;0;3), В(4;1;2) и С(1;-3;2).
Найти площадь треугольника АВС.
Р е ш е н и е. Известно, что площадь треугольника, построенного на векторах и , численно равна половине длины векторного произведения ç ç.
Найдем векторы
и
,
на которых построен треугольник АВС:
(4-2;1-0;2-3)=(2;1;-1),
(1-2;-3-0;2-3)=(-1;
-3;
-1).
Следовательно, по формуле (6) вычисляем:
=
.
Отсюда получаем:
ç
ç=
.
Поэтому искомая
площадь
равна:
ç
ç=
.
О т в е т:
.
П р и м е р 7.
Показать, что точки А(3;2;1),
В(5;1;3),
С(4;4;-2)
и
(6;-2;8)
лежат в одной плоскости.
Р е ш е н и е. Если точки
А,
В,
С
и
D
лежат в одной плоскости, то векторы
и
компланарны.
Это можно выяснить, вычислив их смешанное произведение, поскольку известно, что три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Итак, найдем координаты
векторов
,
и вычислим по формуле (7) их смешанное
произведение:
;
;
;
.
Следовательно, точки А(3;2;1), В(5;1;3), С(4;4;-2) и
(6;-2;8) лежат в одной плоскости.
О т в е т: точки А, В, С и D лежат в одной плоскости.
8. П Р И М Е Р Ы
1. Найти длину и направление (направляющие косинусы) вектора
,
если
Проверить коллинеарность векторов:
Выяснить, как они направлены относительно друг друга; какой из них длиннее и во сколько раз.
3. Даны
точки:
и
.
Доказать, что ABCD трапеция.
4.
Найти разложение вектора
по векторам
и
5.
Найти скалярное произведение
,
если
6. Даны векторы:
Найти угол
между векторами
и
7. Векторы
и
образуют угол
=
=1.
Найти угол между
векторами
и
,
если
8. Даны четыре точки:
Доказать, что диагонали четырехугольника ABCD перпендикулярны.
9. Даны векторы:
.
Найти проекцию
вектора
на направление вектора
.
10. Найти проекцию вектора =(5;1;-1) на ось, составляющую
с координатными осями равные острые углы.
11. Известны
длины векторов ç
ç=5,
ç
ç=6,
а также угол между ними
.
Найти длину их векторного произведения.
12. Даны векторы:
и
Найти длину и направление (направляющие косинусы) их векторного произведения.
13. Найти длину векторного произведения векторов и , если известно, что
ç
ç=10,
ç
ç=2,
12.
14. Даны
два вектора:
.
Известно, что
ç
ç=2,
ç
ç=3,
.
Найти:
;
2)
.
15. Даны точки А(2;3;1), В(4;4;0) и С(3;1;-1). Найти:
1)
3) площадь
2)
4) высоту
в
16. Найти смешанное произведение векторов , и , если:
17.
ç
ç=6,
ç
ç=3,
ç
ç=3,
Найти
18. Установить, компланарны ли векторы:
1)
;
2)
;
3)
.
19. Даны точки: А(1;3;5), В(2;-1;0), С(3; -2; -3) и D(0;1; -1). Найти объем пирамиды DАВС и длину ее высоты DO.
20. Доказать, что точки
А(1;1;5), В(2;3;6), С(4; -1;0) и D(3;0;2)
лежат в одной плоскости. Найти площадь четырехугольника АВСD.
21. Найти
объем параллелепипеда
,
если известны точки А
(2;
-1;1),
В(5;5;4),
С(3;2;
-1),
(4;1;3).
22. Даны три вершины тетраэдра:
А(2;-1;4), В(0;1;3), С(-5;0;1).
Объем тетраэдра равен 7. Найти его четвертую вершину D, если известно, что она лежит на оси абсцисс.
♦ ♦ ♦
23. Может ли некоторый вектор образовать с осями координат углы:
1)
2)
?
24.
Найти разложение вектора
по векторам
и
25.
Векторы
и
образуют угол
.
Зная, что
=3, =4, вычислить:
1)
2)
3)
4) 
;
5)
.
26. Вектор коллинеарен вектору =(2;3;-6) и составляет с осью Oy тупой угол. Найти координаты вектора , если его длина равна 21.
27. Проверить, что является равнобедренным, если
,
Найти углы треугольника.
Даны точки: А(-4;-2;3) и В(5;-2;2). Найти проекцию вектора на ось, составляющую с осями Ox и Oy , соответственно, углы
и
,
а с осью Oz
тупой угол
.
Даны векторы:
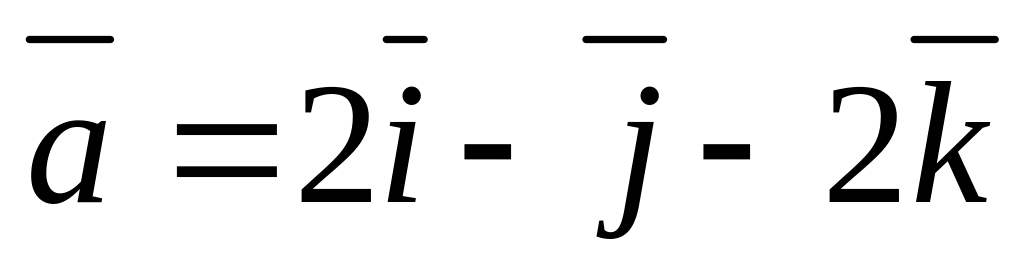и
.
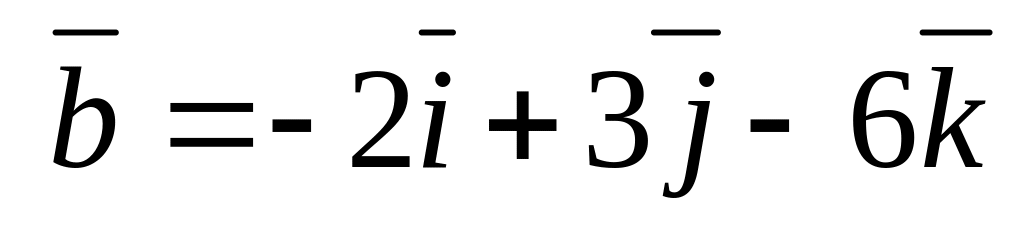Найти:
1
)
2) 
;
3)
;
4)
.
Даны точки:
и
.
Найти:
;
2)
.
31.
Известно, что
=3,
=4,
.
Найти длины векторов:
1)
;
2)
.
32.
Даны векторы
и
Найти:
1)
;
3)
;
2)
;
4)
.
33. Даны
точки:
.
Найти вектор
.
34. Даны вершины треугольника АВС:
.
Найти площадь треугольника АВС и его высоту ВD.
35.
Найти вектор
,
перпендикулярный векторам
и
,
удовлетворяющий условию:
36. Найти смешанное произведение векторов , и , если:
1)
;
2)
.
37. Найти объем параллелепипеда, построенного на векторах
;
и
.
38. Векторы , и , образующие правую тройку, взаимно перпендикулярны. Зная, что =4, =2, =3, вычислить их смешанное произведение .
39. Объем тетраэдра равен 5, три его вершины известны:
,
и
.
Найти его четвертую
вершину D,
если она лежит на оси
.
40. Доказать, что точки
А(1;2;1), В(0; 1;5), С(1; 2; 1) и D(2;1; 3)
являются вершинами параллелограмма. Найти углы и площадь этого параллелограмма.
9. О Т В Е Т Ы
1.
=3;
2
.
=3
.
3.
,
.
4.
5.
=10.
6.
.
7.
8.
9.
10.
11. 15.
12.
=
;
13. 16. 14. 1) 27; 2) 243.
15.
.
16.
1) 1; 2) 5. 17.
18. 1) Да; 2) нет; 3) да.
19.
20.
.
21. 54.
22.
.
23. 1) Нет; 2) да.
24.
25. 1)
6;
2) 13;
3) 61;
4)
5)
26.
27.
=
;
28.
29. 1)
68;
2)
3)
4)
30.
1)
2)
31. 1)
168;
2) 36.
32. 1)
,
2)
,
3)
,
4)
.
33.
.
34.
35.
.
36. 1)
–6;
2) 2.
37. 7. 38. 24.
39.
(0;0;–1),
(0;0;11).
40.
