
- •Глава 1. Оператор Лизеганга
- •Оператор Лизеганга как отражение колебательных свойств гелевых полимерных систем. Введение оператора Лизеганга.
- •1.2.Исследование сильно нелинейного уравнения диффузии
- •1.3. Упрощённая запись оператора Лизеганга
- •Графики для разных значений и . На графике слева приведены значения , справа - . По оси абсцисс отложено время, по оси ординат – значение в безразмерных единицах.
- •График стационарного решения задачи (1.3.5)-(1.3.6). По оси абсцисс отложена безразмерная координата X, по оси ординат – функции и , согласованные при , также в безразмерных единицах.
- •1.5 Оператор Лизеганга и некоторые экспериментальные данные
- •Глава 2 Оптические свойства гелевых оксигидратов и размеры кластеров
- •2.1 Уравнение поглощения света на конформерных “шумовых” кластерах.
- •Концентрационная зависимость кластеров от времени для простейшей спирали.
- •Изменение интенсивности волн прошедшего поля через оксигидратные кластеры в пространстве.
- •2.3 Влияние пульсационного шума или тока самоорганизации в магнитном поле на особенности оптических характеристик окигидрата иттрия.
- •2.4 Кинетические кривые оптической плотности некоторых гелей оксигидратных систем
- •Спектры поглощения силикагелей
- •2.5. Интерферационный подход к экспериментальнолму определению
- •2.6. Вычисления размеров кластеров на примере гелей оксигидрата кремния и иттрия.
- •Зависимости оптической плотности смешанных гелей оксигидрата кремния и оксигидрата иттрия от времени.
- •Глава 3 Каустики стохастических потоковых кластеров и решение задачи формообразования самих кластерных частиц.
- •Глава 4. Каустики лагранжевых отображений гелевой оксигидратной магнитной жидкости железа
- •4.1 Введение
- •4.2 Типичные перестройки каустик в трехмерном пространстве лагранжева многообразия
- •Литература
- •Глава 5 Форма и механизм разряда волновых стохастических кластеров вблизи регистрирующих электродов
- •Результаты и их обсуждение
- •Волновые домены гелей оксигидрата железа,
- •Фазовые портреты двух доменов, указанных стрелками
- •Оксигидрат железа (III)
Глава 2 Оптические свойства гелевых оксигидратов и размеры кластеров
`В данной главе рассматриваются изменения оптической плотности в гелевых оксигдратных системах d- и f- элементов. Приводится связь этих изменений с оператором Лизеганга.
Опираясь на экспериментальные данные и данные расчётов, которые приведены в данной главе, делается вывод о влиянии тока самоорганизации в магнитном поле на особенности оптических характеристик оксигидратных систем. Предлогается метод оценки рзмеров кластеров оксигидратных систем в дисперсионной среде.
2.1 Уравнение поглощения света на конформерных “шумовых” кластерах.
В гелевых оксигидратных системах d- и f- элементов [1-5, 13] наблюдается необычное поведение оптической плотности, которая меняется сложным образом, почти волнообразно - периодически. Возникает вопрос о том, чем определяются такие изменения оптических свойств и как они коррелируются с вопросами, затрагиваемыми в книге? Как нам представляется, внутренний шум, производимый гелевой оксигидратной системой, и ответственен за особенности ее оптических свойств. Кластерная шумовая атмосфера коллоидно-химической системы непосредственно определяется, то есть связана с макромолекулярным строением осадка. Исследовать же строение оксигидратных гелей – это в то же время исследовать механизм синхронизации этих стохастических систем, то есть выявить шумовое влияние оксигидрата, например, на оптические свойства, сорбционные и другие [14-17, 18-28].
Постановка задачи.
Прежде
всего
будем
исходить из того обстоятельства, что
свет гелевой фазой поглощается. При
этом предположим, что зашумленный гель
имеет коэффициент поглощения
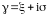 ,
где
,
где
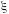 - вещественная часть коэффициента
поглощения, а
- вещественная часть коэффициента
поглощения, а
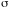 - комплексная, ответственная за поглощение
света веществом.
- комплексная, ответственная за поглощение
света веществом.
Тогда уравнение Гельмгольца для прохождения света через гель примет вид:
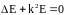
с
условиями стремления решения к нулю на
бесконечности. Здесь используются
следующие обозначения:
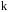 - волновой вектор,
- волновой вектор,
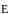 - электромагнитное поле.
- электромагнитное поле.
Выясним,
как волновой вектор зависит от характера
изучаемого вещества. Обычно считается,
что
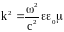 ,
где
,
где
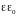 - диэлектрическая проницаемость, а
- диэлектрическая проницаемость, а
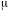 - магнитная проницаемость. Обычно принято
считать, что магнитная проницаемость
мало влияет на изменения в электромагнитном
поле, так как магнитное поле электромагнитной
волны невелико. Будем считать, что оно
действительно мало, а поэтому магнитная
проницаемость принимается нулевой. Что
касается диэлектрической проницаемости,
то, согласно определению, в веществе
- магнитная проницаемость. Обычно принято
считать, что магнитная проницаемость
мало влияет на изменения в электромагнитном
поле, так как магнитное поле электромагнитной
волны невелико. Будем считать, что оно
действительно мало, а поэтому магнитная
проницаемость принимается нулевой. Что
касается диэлектрической проницаемости,
то, согласно определению, в веществе
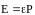 ,
где
,
где
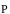 - вектор поляризации среды. Вначале
поступим простейшим способом: будем
считать, что
- вектор поляризации среды. Вначале
поступим простейшим способом: будем
считать, что
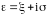 в вышеописанных обозначениях. То есть
будем считать, что свет поглощается
гелевой фазой оксигидрата, но учитывать
вторичные последствия этого поглощения
мы не будем. Хотя, естественно, эти
взаимодействия существенны, нами
понимаются и исследованы достаточно
подробно в работах [1, 2, 22, 23].
в вышеописанных обозначениях. То есть
будем считать, что свет поглощается
гелевой фазой оксигидрата, но учитывать
вторичные последствия этого поглощения
мы не будем. Хотя, естественно, эти
взаимодействия существенны, нами
понимаются и исследованы достаточно
подробно в работах [1, 2, 22, 23].
Тогда необходимо рассмотреть следующую краевую задачу (рис.2.1):
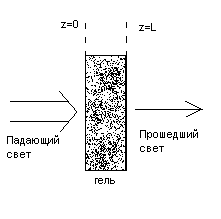
Рис. 2.1
Область решения задачи для поглощения света в геле.
Будем считать, что на стенке
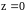 задано одно краевое условие, на стенке
задано одно краевое условие, на стенке
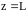 - условие для прошедшего света. Проблема
состоит в том, что мы этого второго
условия не знаем.
- условие для прошедшего света. Проблема
состоит в том, что мы этого второго
условия не знаем.Всюду в области
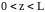 волновой вектор определяется как
волновой вектор определяется как
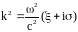 .
.Всюду за пределами области (мы её назовём областью
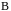 )
волновой вектор определяется соотношением
)
волновой вектор определяется соотношением
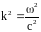 .
.
Таким образом, задача имеет вид:
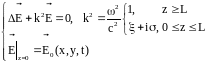 (2.1.1)
(2.1.1)
где
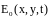 - некоторое значение падающего
электрического поля на границе области,
величина
- некоторое значение падающего
электрического поля на границе области,
величина
 - время, которое в нашей задаче будет
играть роль параметра.
- время, которое в нашей задаче будет
играть роль параметра.
Для
дальнейших обсуждений удобно считать,
что из всех векторов поля остаётся
только поле, направленное по оси
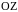 ,
так как гель образован вытянутыми
макромолекулами. Остальные поля можно
просто обозначить через
,
так как гель образован вытянутыми
макромолекулами. Остальные поля можно
просто обозначить через
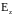 ,
считая, что электрическое поле поляризовано
по кругу, или вообще их не рассматривать.
,
считая, что электрическое поле поляризовано
по кругу, или вообще их не рассматривать.
Тогда задача (1) слегка изменится, и примет вид:
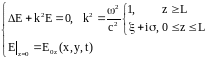 (2.1.2)
(2.1.2)
Далее,
нас интересует поведение поля только
вдоль оси
,
так как мы пренебрегаем связью компонентов
поля. Так как размеры ячейки с гелем
достаточно велики по сравнению с длиной
волны ограничимся только несколькими
первыми гармониками электромагнитного
поля, поэтому отбросим производные по
координатам
 и
и
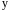 ,
оставив эти переменные только как
параметры. Дело в том, что величины
,
оставив эти переменные только как
параметры. Дело в том, что величины
 будут зависеть от этих координат в силу
плоскостной дипольной морфологии
кластерных диполей в геле. Тогда систему
(2) можно преобразовать к виду:
будут зависеть от этих координат в силу
плоскостной дипольной морфологии
кластерных диполей в геле. Тогда систему
(2) можно преобразовать к виду:
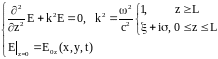 (2.1.3)
(2.1.3)
Условия излучения.
Представляется
удобным отбросить неограниченную
область, в которой волновой вектор
является постоянной величиной. Для
этого можно провести косинус-преобразование
Фурье по отрезку
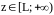 .
В результате получаем соотношение:
.
В результате получаем соотношение:
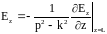 .
Отметим, что в этом соотношении уже
учтена ограниченность решения на
бесконечности.
.
Отметим, что в этом соотношении уже
учтена ограниченность решения на
бесконечности.
В
полученном соотношении обратим
косинус-преобразование Фурье и устремим
 к
к
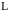 .
В результате имеем:
.
В результате имеем:
 .
(2.1.4)
.
(2.1.4)
Отметим, что в силу пренебрежения разновидностями гармоник можно это соотношение применить к любой гармонике разложения поля по собственным функциям поперечного сечения (по плоским волнам).
Разложение по плоским волнам.
Пусть
для изучения поглощения света предлагается
квадрат со стороной
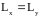 .
Предположим, что на краях квадрата (
.
Предположим, что на краях квадрата (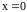 ,
,
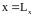 ,
,
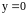 ,
,
 )
поле равно нулю. Тогда для решения задачи
(3) будем искать решение в виде разложения
по поперечным функциям собственного
сечения задачи, то есть будем искать
в виде:
)
поле равно нулю. Тогда для решения задачи
(3) будем искать решение в виде разложения
по поперечным функциям собственного
сечения задачи, то есть будем искать
в виде:
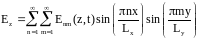 .
.
Отметим,
что, по крайней мере, в первых гармониках
величина
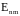 очень незначительно зависит от поперечного
сечения квадрата, поэтому этой зависимостью
можно пренебречь.
очень незначительно зависит от поперечного
сечения квадрата, поэтому этой зависимостью
можно пренебречь.
Для получаем:
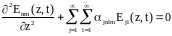 (2.1.5)
(2.1.5)
с
краевыми условиями:
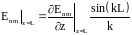 и
и
 .
.
Величины
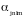 можно вычислить по формулам:
можно вычислить по формулам:
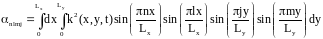 .
.
Некоторые частные случаи.
Рассмотрим
случай, когда нас интересует только
одна гармоника
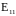 .
Тогда задача (2.1..4) с краевыми условиями
имеет вид:
.
Тогда задача (2.1..4) с краевыми условиями
имеет вид:
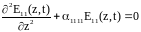 .
.
Её
решение в общем виде -
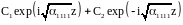 .
Учитывая начальное условие
.
Учитывая начальное условие
 ,
получаем:
,
получаем:
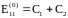 .
Далее, из второго краевого условия
получаем:
.
Далее, из второго краевого условия
получаем:
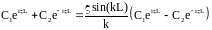 ,
или
,
или
 ,
где
,
где
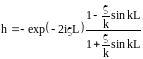 ,
,
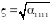 .
Отсюда
.
Отсюда
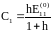 ,
,
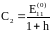 .
.
Вычислим
теперь, насколько количественно
поглощается электромагнитное поле
гелем. Отметим, что
 .
Следовательно,
.
Следовательно,
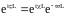 ,
,
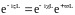 .
Если считать, приближённо, что
.
Если считать, приближённо, что
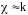 ,
,
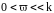 ,
то
,
то
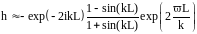 ,
то есть величина
,
то есть величина
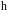 увеличивается в
увеличивается в
 раз.
раз.
Далее,
 ,
то есть множитель
,
то есть множитель
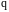 появится следующим образом:
появится следующим образом:
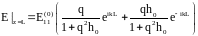 .
Если
значителен, то электрическое поле можно
будет грубо оценить как
.
Если
значителен, то электрическое поле можно
будет грубо оценить как
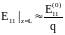 .
.
2.2 Связь с оператором Лизеганга.
Пусть
теперь
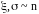 ,
где
,
где
 -
текущая концентрация гелевых нанокластеров
(
-
текущая концентрация гелевых нанокластеров
(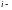 нанокластеров,
то есть нанокластеров
размера) в геле. Следовательно,
нанокластеров,
то есть нанокластеров
размера) в геле. Следовательно,
 .
Если концентрация меняется по закону,
предписываемому оператором Лизеганга
[23, 24], то прошедшее электрическое поле
будет меняться по соответствующему ему
закону, например, так, как это изображено
на рис. 2.2 и 2.3.
.
Если концентрация меняется по закону,
предписываемому оператором Лизеганга
[23, 24], то прошедшее электрическое поле
будет меняться по соответствующему ему
закону, например, так, как это изображено
на рис. 2.2 и 2.3.
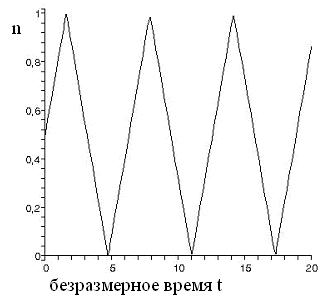
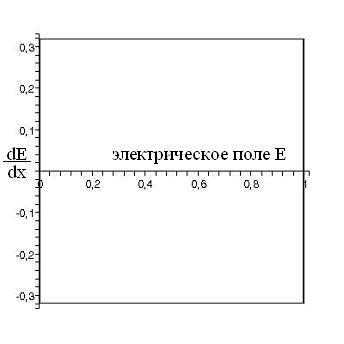
Рис.2.2 Вид оператора Лизеганга.
Рисунок слева – изменение концентрации нанокластеров с течением времени. По оси абсцисс – время в безразмерных единицах, по оси ординат – безразмерная концентрация, задаваемая оператором Лизеганга. Рисунок справа – фазовая диаграмма электрического поля в прошедшей волне. По оси абсцисс– электрическое поле в безразмерных единицах.
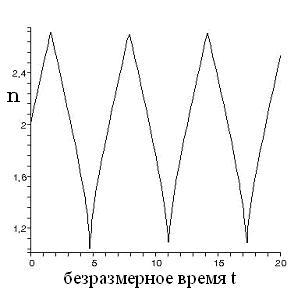
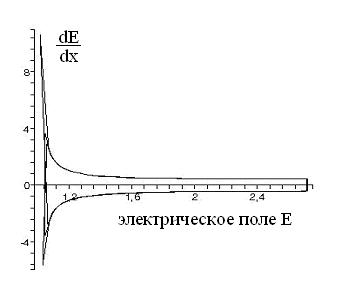
Рис.2. 3 Оператор Лизеганга и соответствующая ему фазовая диаграмма прошедшего поля.
Рисунок слева – безразмерная концентрация в зависимости от безразмерного же времени (от рис. 2.2 отличается величиной концентрации). Справа – фазовая диаграмма соответствующего этой концентрации поля в прошедшей волне. По оси абсцисс – само поле, по оси ординат – его производная по координате.
Просто плоская волна.
Теперь
рассмотрим случай, когда мы не хотим
решать вопрос о том, надо ли разбивать
волну на отдельные гармоники. Будем
считать просто, что на нас падает самая
обычная плоская волна. Тогда решение
изменится только в отношении того, что
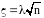 ,
будет зависеть ещё и от
,
будет зависеть ещё и от
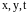 .
.
,
(2.2.1)
Нас
интересует отношение интенсивности на
выходе из гелевой среды к интенсивности
на входе,
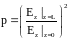 .
Соответственно, учитывая вычисления,
сделанные в предыдущем параграфе, это
соотношение мы можем оценить как
.
Соответственно, учитывая вычисления,
сделанные в предыдущем параграфе, это
соотношение мы можем оценить как
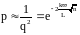 .
Отметим, что эта интенсивность, вероятнее
всего, распределена по пространству.
Нас поэтому интересует интеграл от неё
по некоторой области, то есть коэффициент
прохождения света будет иметь вид:
.
Отметим, что эта интенсивность, вероятнее
всего, распределена по пространству.
Нас поэтому интересует интеграл от неё
по некоторой области, то есть коэффициент
прохождения света будет иметь вид:
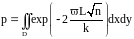 (2.2.2)
(2.2.2)
В результате мы получаем следующие графики:
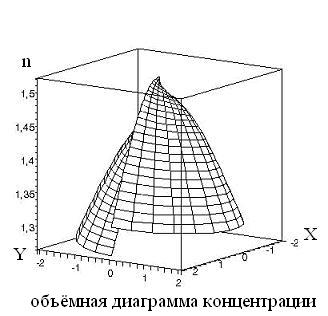
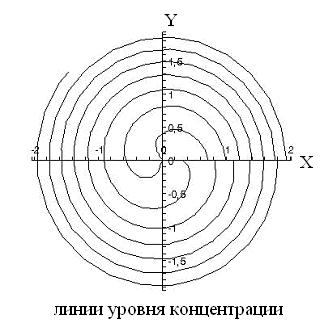
Рис. 2.4
