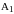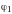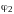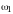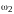- •Глава 1. Оператор Лизеганга
- •Оператор Лизеганга как отражение колебательных свойств гелевых полимерных систем. Введение оператора Лизеганга.
- •1.2.Исследование сильно нелинейного уравнения диффузии
- •1.3. Упрощённая запись оператора Лизеганга
- •Графики для разных значений и . На графике слева приведены значения , справа - . По оси абсцисс отложено время, по оси ординат – значение в безразмерных единицах.
- •График стационарного решения задачи (1.3.5)-(1.3.6). По оси абсцисс отложена безразмерная координата X, по оси ординат – функции и , согласованные при , также в безразмерных единицах.
- •1.5 Оператор Лизеганга и некоторые экспериментальные данные
- •Глава 2 Оптические свойства гелевых оксигидратов и размеры кластеров
- •2.1 Уравнение поглощения света на конформерных “шумовых” кластерах.
- •Концентрационная зависимость кластеров от времени для простейшей спирали.
- •Изменение интенсивности волн прошедшего поля через оксигидратные кластеры в пространстве.
- •2.3 Влияние пульсационного шума или тока самоорганизации в магнитном поле на особенности оптических характеристик окигидрата иттрия.
- •2.4 Кинетические кривые оптической плотности некоторых гелей оксигидратных систем
- •Спектры поглощения силикагелей
- •2.5. Интерферационный подход к экспериментальнолму определению
- •2.6. Вычисления размеров кластеров на примере гелей оксигидрата кремния и иттрия.
- •Зависимости оптической плотности смешанных гелей оксигидрата кремния и оксигидрата иттрия от времени.
- •Глава 3 Каустики стохастических потоковых кластеров и решение задачи формообразования самих кластерных частиц.
- •Глава 4. Каустики лагранжевых отображений гелевой оксигидратной магнитной жидкости железа
- •4.1 Введение
- •4.2 Типичные перестройки каустик в трехмерном пространстве лагранжева многообразия
- •Литература
- •Глава 5 Форма и механизм разряда волновых стохастических кластеров вблизи регистрирующих электродов
- •Результаты и их обсуждение
- •Волновые домены гелей оксигидрата железа,
- •Фазовые портреты двух доменов, указанных стрелками
- •Оксигидрат железа (III)
1.5 Оператор Лизеганга и некоторые экспериментальные данные
Рассмотрим
экспериментальную зависимость
концентрации кластеров в дисперсионной
среде от времени. Пусть известно, что
концентрация вещества в некоторые
моменты времени
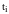 принимала значения
принимала значения
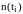 - например, рис.1.7.
- например, рис.1.7.
Рис. 1.7
Экспериментальная зависимость концнтрации оксигидрата металла при фиксированной температуре над осадком.
По
оси абсцисс – единица времени (в сутках),
по оси ординат – концентрация растворенных
кластеров оксигидрата (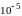 моль на литр). Чёрными точками отмечены
экспериментальные значения, пунктирной
линией – подбор значений в виде ряда
Фурье.
моль на литр). Чёрными точками отмечены
экспериментальные значения, пунктирной
линией – подбор значений в виде ряда
Фурье.
Исходя из экспериментальных значений концентрации во времени можно получить диаграмму зависимости концентрации от времени. Для этого потребуется восстановить производную концентрации [15].
Будем
исходить из того, что концентрация в
произвольный момент времени может быть
представлена в виде ряда Фурье:
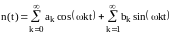 ,
где
,
где
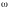 - частота колебаний. При этом нам
достаточно нескольких первых членов
ряда. Производная в этом случае имеет
вид
- частота колебаний. При этом нам
достаточно нескольких первых членов
ряда. Производная в этом случае имеет
вид
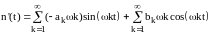 ,
и нам достаточно просто подобрать
коэффициенты
,
и
,
и нам достаточно просто подобрать
коэффициенты
,
и
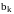 ,
исходя из минимума разности
,
исходя из минимума разности
 .
Отметим, что выбор именно ряда Фурье
для описания связи
и
.
Отметим, что выбор именно ряда Фурье
для описания связи
и
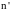 остаётся открытым: можно было бы
использовать многочлены или почти
периодические функции. Так или иначе,
экспериментальные данные можно приблизить
разными способами, и не очевидно, что
выбор именно ряда Фурье – правилен.
остаётся открытым: можно было бы
использовать многочлены или почти
периодические функции. Так или иначе,
экспериментальные данные можно приблизить
разными способами, и не очевидно, что
выбор именно ряда Фурье – правилен.
Для
рисунка 1.7. подбирался следующий ряд:
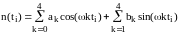 ,
где
,
где
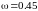 ,
,
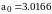 ,
,
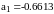 ,
,
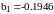 ,
,
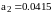 ,
,
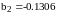 ,
,
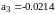 ,
,
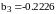 ,
,
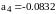 ,
,
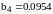 .
Фазовая диаграмма для этого случая
имеет вид:
.
Фазовая диаграмма для этого случая
имеет вид:
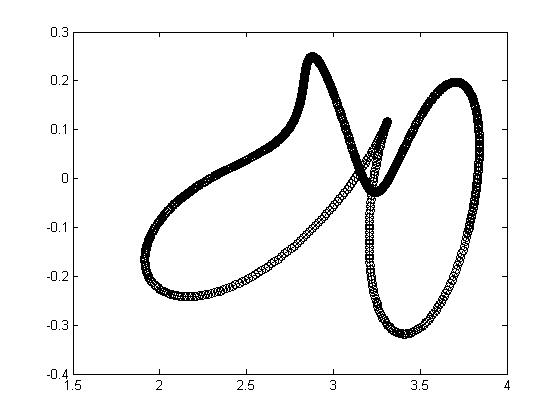
Рис. 1.8.
Фазовая диаграмма связи концентрации и её производной.
По оси абсцисс – концентрация (умноженная на 100000), по оси ординат – её производная, вычисленная дифференцированием ряда.
Исходя из этой диаграммы, можно строить дифференциальное уравнение:
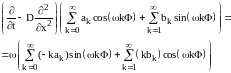
и искать его численное решение. Приведенное уравнение есть не что иное, как общее уравнение Лизеганга (1.1.4).
Здесь возникает целый ряд вопросов, из которых самый важный – вопрос об адекватности построенного уравнения и экспериментальных данных. Выяснить это можно, только сравнивая построенные решения с экспериментом.
Для выяснения соотношения экспериментальных данных и дифференциального уравнения рассмотрим пространственные колебания решения.
Из
вида решения стационарной задачи
следует, что длина половины структуры
будет определяться равенством
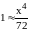 ,
откуда следует, что
,
откуда следует, что
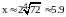 .
Следовательно, весь размер пространственного
периода, учитывая нормировку фрагмента,
будет
.
Следовательно, весь размер пространственного
периода, учитывая нормировку фрагмента,
будет
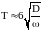 .
Считая диффузию геля
.
Считая диффузию геля
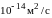 ,
а частоту колебаний равной примерно
,
а частоту колебаний равной примерно
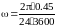 Гц, получим приблизительное равенство
Гц, получим приблизительное равенство
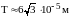 ,
т.е. около одной десятой-сотой сантиметра.
Это не противоречит экспериментальным
данным.
,
т.е. около одной десятой-сотой сантиметра.
Это не противоречит экспериментальным
данным.
Заметим, что колебания не обязательно могут быть описаны с помощью именно ряда Фурье. Возможно, частоты некратные. Для получения ответа на этот вопрос построим спектр частот экспериментальных данных.
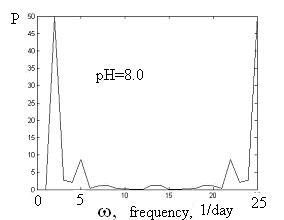
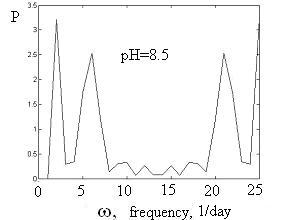
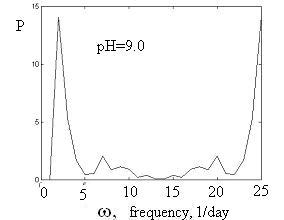
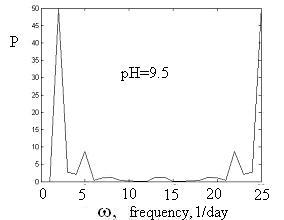
Рис. 1.9
Графики
диаграмм мощности для разных pH.
По оси абсцисс – частоты в 1/сут (т.е. в
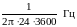 )
)
Приближение набором кривых получается достаточно точным:
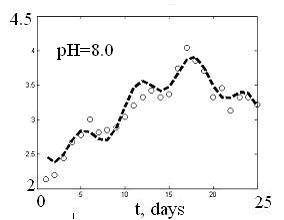
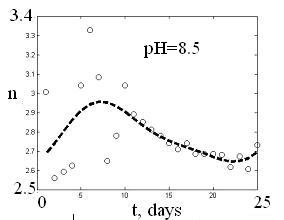
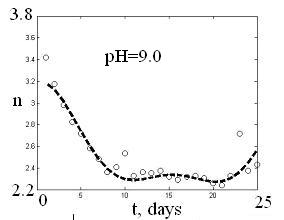
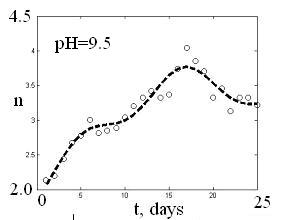
Рис. 1.10
Графики приближений получены методом наименьших квадратов для соответствующих графиков рис.1.9. Значения подобранных коэффициентов приведены ниже в таблице. Нумерация графиков – слева направо и сверху вниз. Кружками обозначены экспериментальные значения, пунктирная линия – результат решения задачи подбора.
Таблица 1.
Значения
коэффициентов для графиков рисунков
1.9 и 1.10. Общая формула:
 ,
где коэффициенты следует взять из
таблицы, а значение
,
где коэффициенты следует взять из
таблицы, а значение
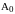 - среднее значение экспериментальных
данных.
- среднее значение экспериментальных
данных.
|
|
|
|
|
|
|
1-ый график |
5.7437 |
2.0465 |
2.5272 |
-1.3592 |
0.2191 |
-0.9841 |
2-ой график |
0.1495 |
-0.0438 |
3.9689 |
0.2944 |
0.2681 |
0.4892 |
3-ий график |
-2.6976 |
-2.5220 |
1.6368 |
4.5119 |
0.2974 |
0.3147 |
4-ый график |
1.0830 |
0.1859 |
4.2393 |
-2.5276 |
0.1126 |
0.5294 |
Теперь
рассмотрим взаимосвязь гидродинамического
рассмотрения и оператора Лизеганга.
Несколько ранее построены некие
пространственные структуры, основанные
на использовании простейшего оператора
Лизеганга с круговой диаграммой.
Концентрация кластеров металла в этом
случае относительно фона имеет вид:
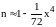 ,
,
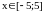 .
Добавим фон в виде произвольного
небольшого множителя
.
Добавим фон в виде произвольного
небольшого множителя
 .
.
Подход
с введением оператора Лизеганга
получается из гидродинамического
рассмотрения заменой величины
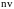 в уравнении непрерывности на
в уравнении непрерывности на
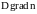 .
Следовательно, в одномерном случае мы
можем записать, что
.
Следовательно, в одномерном случае мы
можем записать, что
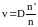 ,
или
,
или
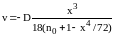 .
Уравнение для скоростей может быть
записано как
.
Уравнение для скоростей может быть
записано как
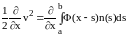 .
Учитывая явное выражение для концентрации
,
получим интегральное уравнение для
нахождения потенциала взаимодействия
фрагментов между собой и средой. Это
интегральное уравнение может быть
решено и точно, и численно. Численное
решение имеет вид:
.
Учитывая явное выражение для концентрации
,
получим интегральное уравнение для
нахождения потенциала взаимодействия
фрагментов между собой и средой. Это
интегральное уравнение может быть
решено и точно, и численно. Численное
решение имеет вид:
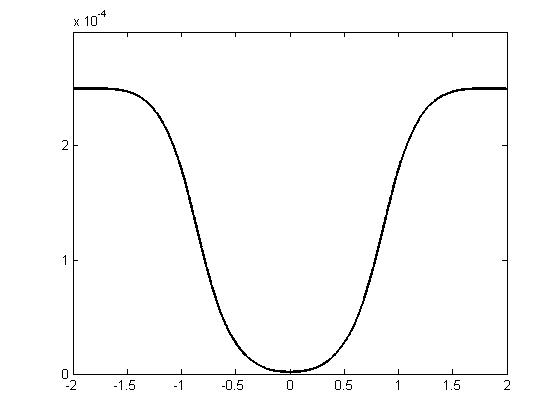
Рис.1.11
График изменения потенциала в зависимости от координат.
Отметим, что глубина полученной потенциальной ямы определяется величиной фона и экспериментально найденной частотой. График соответствует прямоугольной потенциальной яме с размытыми, гладкими краями. Следовательно, использование функций синуса и косинуса для представления оператора Лизеганга имеет под собой основания.
Более точные вычисления выходят за рамки настоящего изложения.
Выводы
1.
Таким образом, гелевые системы являются
системами живущими, закономерно
развивающимися во времени.
Налицо спиралеобразное движение
кластерных ионных потоков (или торовое)
в гелевой дисперсионной среде.
Становится более понятным периодический
характер изменения реологических
параметров геля (
)
(скорости сдвига) от касательных
напряжений ( ).
Периодический характер изменения
реологических кривых, сорбционных
свойств и других определяется фазовым
разнообразием геля, который меняется
во времени.
).
Периодический характер изменения
реологических кривых, сорбционных
свойств и других определяется фазовым
разнообразием геля, который меняется
во времени.
Такое развитие ситуации происходит для микрогетерогенных коллоидных систем. Именно эта ситуация возникает на границе раздела фаз в золь-гель процессах. Любая гелевая система непременно имеет подобную границу раздела фаз. Связь между элементами среды (осуществляемая, например, благодаря диффузии в межмицеллярном растворе) не имеет принципиального значения для распространения быстрых фазовых волн, когда градиенты фазы достаточно малы.
Очевидно, высушивание (обезвоживание) подобных систем так или иначе должно зафиксировать генезис их предыдущей истории, то есть развития в активный период их “пульсационной” жизни в гелевом подвижном состоянии. Эти исследования можно выполнить только экспериментально. Это отражение активного “пульсационного” периода генезиса геля достаточно сложно и противоречиво.
2. Осуществлена общая аналитическая запись оператора Лизеганга, отражающего пульсационно – периодический генезис гелевого состояния оксигидратаов.. Самая общая форма записи сильно нелинейного дифференциального уравнения Лизеганга с точки зрения математической формы имеет вид:
, .
Заметим, что в этом случае запись оператора Лизеганга в явной форме затруднительна, а в неявной – задаётся парой парметрических соотношений:
или общим оператором Лизеганга является выражение через , где ,
.
3. Анализ оператора Лизеганга позволил определить полуразмер области структурирующего взаимодействия нанокластеров оксигидратной системы:
.
В этом соотношении имеет размерность частоты спайковых выплесков оксигидратных кластеров.
Литература.
15. Шемякин Ф.М., Михалев П.Ф. Физико-химические периодические процессы.- М: Изд. АН СССР, 1938. 183с.
Сухарев Ю.И., Егоров Ю.В. Неорганические иониты типа фосфата циркония. - М.: Энергоатомиздат, 1983. 142с
Yuri I. Sucharev. Nonlinearity of Colloid Systems: Oxyhydrate Systems. Switzerland, UK, USA: Trans Tech Pulications, (2007). P. 433
4.Сухарев Ю.И. Нелинейность гелевых оксигидратных систем
/Ю.И.Сухарев, Б.А.Марков.- Екатеринбург: УРО РАН , 2005. 468с.
Сухарев Ю.И., Апаликова И.Ю., Тарамина Е.В., Азаров М.Б. Каустикти лагранжевых отобрапжений гелевой оксигидратной магнитной жидкости железа. Бутлеровские сообщения. 2012.Т.31. N 8.С.1012-116.
6. 30. Y. I. Sukharev and B. A. Markov. Liesegang rings as the common gross property of oxyhydrate and other gel polymer systems: another look at the problem of periodicity // Molecular Physics, 2004. V.102, № 7. P.745-755
7. 31.Yuri I. Sukharev, T.G.Krupnova, E.P.Yudina, I.Yu. Lebedeva. Concerning the interconnections of self-organizing oxyhydrate gels and their experimental determination // Colloids and Surfaces A: Physicochem. Eng. Aspects 2007- . 300. С. 281-286
8.Заславский Г.М. Слабый хаос и к4вазирегулярные структуры/ Г.М. Заславский и др. М.: Наука, 1991. 235с.
9. А.Н. Боголюбов, Н.Н. Кравцов, А.Г. Свешников «Лекции по уравнениям математической физики». М., МГУ. 1993 г. С. 356.
10. А.Н. Тихонов, Арсеньев В.Я. «Методы решения некорректных задач».М.: Наука, 1979, с.288
11. Yury Sucharev and V.A. Potyomkin. Formation of structuring elements of zirconium oxyhy-drate gels under unbalanced conditions // Chemistry Preprint Archive, Volume 2002, Issue 4, April 2002. P. 108-128
12. Б.А.Марков, Ю.И.Сухарев,В.А.Потемкин, В.В.Авдин, Е.А.Короткова. Моделирование автоволновых процессов формообразования оксигидратных гелей тяжелых металлов // Математическое моделирование, 1999. Т. 11, N012. С.1720
13 . Yuri I. Sucharev. Wave Oscillations in Colloid Oxyhydrates // Switzerland, UK, USA: Trans Tech Publications LTD. 2010. 497p.
14. А.Н. Боголюбов, Н.Н. Кравцов, А.Г. Свешников «Лекции по уравнениям математической физики». М., МГУ. 1993 г. С. 356.
15. Сухарев Ю.И. Оператор эволюции Лизеганга оксигидратных гелей как главный фактор изменения оптической плотности/Ю.И.Сухарев, Б.А.Марков//Изв.Челяб.науч.центра УроРАН.2005.№1.