Графики для разных значений и . На графике слева приведены значения , справа - . По оси абсцисс отложено время, по оси ординат – значение в безразмерных единицах.

Из графиков следует, что при достаточно больших значениях времени решение растёт неограниченно, что противоречит эксперименту и здравому смыслу. Однако при некоторых значениях параметров – размера области, диффузии и коэффициента существует и стационарное решение (т.е. предел ). В том же случае, когда необходимо построить нестационарное решение, следует рассматривать область с подвижной границей.

Стационарное решение. Рассмотрим теперь стационарное решение. Задачи (1.3.1) и (1.3.2) в этом случае примут вид:

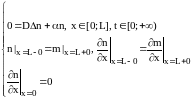(1.3.4)

(1.3.5)

Решение (1.3.5) имеет вид: , следовательно, задача (1.3.5) может быть переписана как задача со следующим краевым условием:

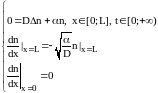(1.3.6)

и решение (1.3.6) записывается: 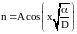. Из краевого условия на границе получаем: 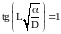, откуда . Заметим, что, так как концентрация по смыслу задачи неотрицательна, то . Из условий согласования следует, что 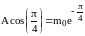, т.е. . График решения приведён на рис.5.5. XI. Из рис. 5.5 XI следует, что в точке согласования и в точке максимума величины относятся друг к другу как . Кроме того, можно определить полуразмер области структурирующего взаимодействия – это

. (1.3.7)

В этом соотношении имеет размерность частоты.

Полученное красивейшее соотношение весьма многозначно, ибо оно практически совпадает с ранее рассмотренным и полученным выражением для 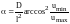в разделе 2.4 [13]. Оценочно можно полагать, что размеры структурных элементов гелевой системы равны . То есть разные подходы к рассмотрению идеи оператора Лизеганга дали практически одинаковые размеры структурно- кластерных элементов. Они приведены в таблице 2.1 [13].

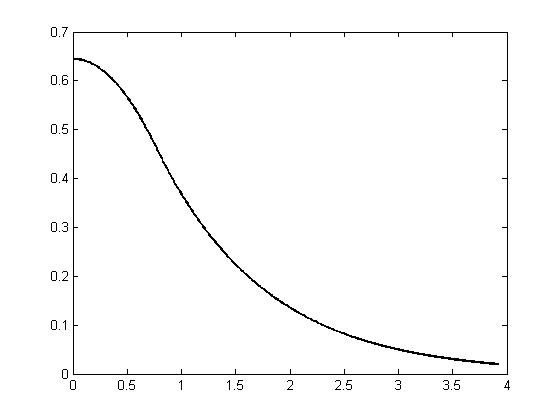
Рис.1.5

График стационарного решения задачи (1.3.5)-(1.3.6). По оси абсцисс отложена безразмерная координата X, по оси ординат – функции и , согласованные при , также в безразмерных единицах.

Выясним теперь, может ли быть у области более одного максимума. Пусть максимумов два, и они разделены интервалом, где наблюдается спад концентрации ( рис. 5.6).

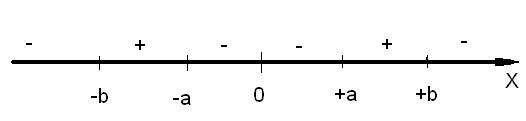
Рис. 1.6

Расположение знаков правой части по отрезку.

Рассмотрим следующую задачу:

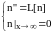
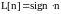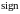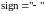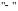где , а - знак, соответствующий рис.5.6 12. Т.е. , если , , если , , если 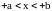, , если , , если 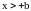. В точках разрыва поставлено условие согласования – непрерывность решения и его первой производной по координате.

Условия согласования дадут следующие условия для параметров: .

Выясним теперь, как будет относиться решение в точке к решению в точке 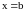. Верно следующее утверждение:

Утверждение. Решение существует, если .

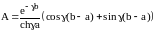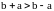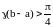Доказательство. Действительно, условия согласования дают связь амплитудных коэффициентов . С учётом связи коэффициентов получаем: . Заметим, что , следовательно, , т.е. . Тогд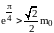а, , отсюда .

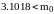То есть выясняется интересный факт: чтобы существовало решение, необходимо, чтобы в нуле оно было меньше, чем на внешней стороне более чем в три раза!

Физический смысл упрощённого оператора Лизеганга.

Физический смысл упрощённого оператора Лизеганга состоит в том, что в одномерном случае упрощённый оператор Лизеганга определяется электростатическим взаимодействием. Действительно, пусть существует система уравнений [14] :

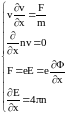
Ищем 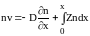. Тогда уравнение даст соотношение 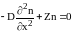. Интегрируя уравнение 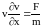, получим 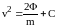, откуда 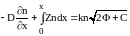. Дифференцируя обе части по , имеем 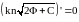. Отсюда , как и для электростатической задачи.

Учитывая решение задачи для потенциала

,

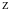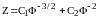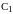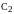получаем связь функции с электрическим потенциалом: , где числа и должны быть получены из интегрирования задачи.

Таким образом, несложно видеть, что для упрощённой записи мы просто объявляем постоянной того или иного знака. Отметим, что такое приближение является достаточно неточным, но при определённых значениях постоянных и знак может действительно меняться. Отметим, что более точное выражение для (например, приближение многочленами) приведёт лишь к изменению формы гармоник (рис.1.5), но вряд ли – к радикальному изменению поведения решения задачи.

1.4. Гидродинамический подход

Для описания колебаний можно взять простые периодические функции – синус и косинус. Будем считать, что такой выбор функций обусловлен грубостью эксперимента и слишком большим количеством неизвестных параметров. Так, неизвестен потенциал взаимодействия гелевых фрагментов, то нам его предстоит найти. Если же взять простейший, модельный, вид потенциала – прямоугольная потенциальная яма – то колебания тепловых энергий будут иметь вид ряда по синусам и косинусам. Пренебрегая членами малого порядка, можем убедиться в допустимости такого выбора. Чтобы доказать приведённое выше утверждение, рассмотрим полную задачу.

Пусть коллоидные кластеры взаимодействуют друг с другом с потенциалом 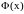, который представляет собой потенциальную яму некоей максимальной глубины . Отметим, что выделить отдельно взаимодействие коллоидных фрагментов между собой и коллоидных фрагментов со средой мы не можем, поэтому поместим в этот потенциал и взаимодействие со средой, или учтём среду с помощью динамической вязкости. Тогда, так как взаимодействие происходит в дисперсионной среде, то для скорости коллоидных фрагментов 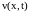в данной точке пространства в данный момент времени можно написать гидродинамическое уравнение 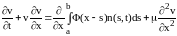, где - концентрация геля, 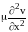- динамическая вязкость. Вторым уравнением возьмём уравнение непрерывности, полагая, что фрагменты мало взаимодействуют друг с другом: 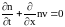. Для того, чтобы система дифференциальных уравнений была завершённой, добавим начальное и краевое условия. Окончательно получаем:

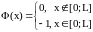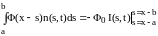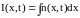Заметим, что, считая потенциал прямоугольной ямой , можно записать: , где . Будем также считать, что потенциал взаимодействия гелевых фрагментов невелик (это соответствует экспериментальным данным: колебания действительно малы), и величину можно рассматривать как малый параметр.