Результаты и их обсуждение

Толчковые явления перемещения нанокластеров в пространстве образуют спиралевидные волны, представленные в таблице 2,3. Из рассмотренных нами ранее задач [17] следует, что структурным элементом коллоидного геля является фрагмент спирали. Эта спираль обладает дипольным моментом и, при достаточно близком рассмотрении, может быть представлена как стохастический круг.

Ранее нами было рассмотрена задача, связанная с поведением малых частиц геля-кластеров [17]. В геле постоянно происходят диссоциативно-диспропорциональные [14] толчковые явления с выбросом третьих кластерных (в основном нанокластерных) частиц, которые отвечают за диссипацию энергии системы. Отщепление отдельных частиц геля, которые могут быть заряженными, либо их присоединение к крупным фрагментам макромолекул, от которых ранее они отщепились, инициируют токовые периодические пульсации [18].

Отщепившиеся третьи заряженные кластеры геля перемещаются в пространстве под воздействием электрического поля. Представляется логичным считать, что взаимодействие свободного заряженного гелевого фрагмента и электрического поля определяется линейной формулой 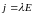, где - вектор тока, 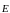- электрическое поле, число - некоторый коэффициент пропорциональности. Это означает, что, зафиксировав вектор тока, мы можем указать и вектор поля.

Заметим, что вектор электрического поля есть градиент потенциала. Следовательно, если мы знаем электрическое поле в каждой точке пространства, то мы можем построить и эквипотенциали, проводя линию всякий раз перпендикулярно направлению электрического поля: эквипотенциаль и электрическое поле взаимно-перпендикулярны.

Задача об эллипсе. Теперь рассмотрим следующую задачу. Положим, существует аксиально-симметричный потенциал. Его линии представляют собой концентрические круги (рис. 4).

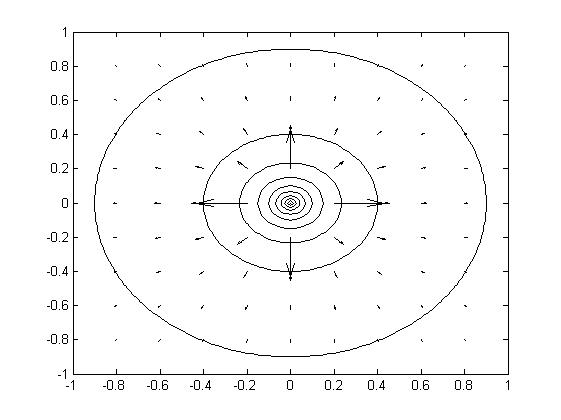
Рис. 5.4.

Эквипотенциали аксиально-симметричного потенциала.

Стрелками обозначено направление поля.

Из рисунка видно, что вектор поля направлен перпендикулярно к эквипотенциали, и в то же время все векторы поля пересекаются в центре круга.

В том случае, если мы рассматриваем задачу с двумя свободными зарядами, но различно поляризованными, то поле принимает иной вид (рис.5.) Причину поляризации рассматривать не будем, она практически ясна.

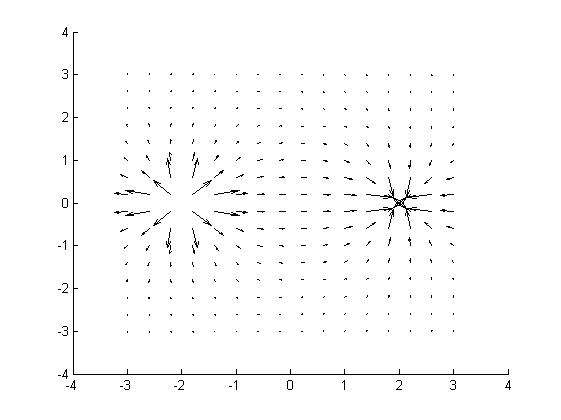
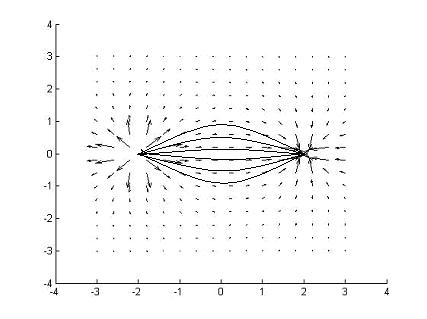
Рис.5.5.

Эквипотенциали диполя.

Эквипотенциали квадруполя очевидно имеют следующий вид, рис.6:

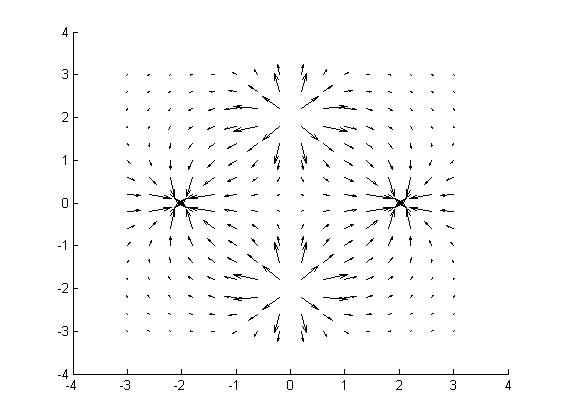
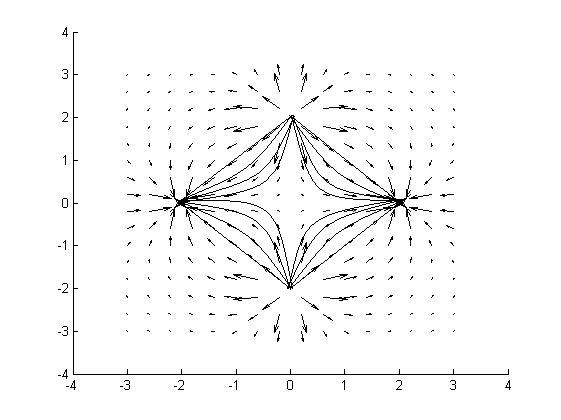
Рис.5.6.

Эквипотенциали квадруполя.

В области между зарядами векторы поля образуют веретено (стрелками обозначено направление поля). Таким образом, если мы имеем экспериментальную карту полей, по которой можно визуально установить, имеем ли мы дело с диполем или с квадруполем. И, если мы можем построить векторную диаграмму токов, а затем предположив, что токи линейно связаны с полями, то по геометрии токов (потоков кластеров) можно определить конфигурацию взаимодействующих зарядов. А это уже энергетическая характеристика типа лагранжиана [19]

Процесс распространения энергетических возмущений гелевой системы описывается системой лучей [1,2]. Например, распространение возмущений внутрь эллипса можно представить семейством внутренних нормалей к эллипсу, которое имеет огибающую, называемой каустикой. Близкий к эллипсу фронт имеет каустику с такими же особенностями, а именно четырьмя точками возврата. Все более сложные особенности каустик рассыпаются при малом шевелении на стандартные особенности: точки возврата и точки самопересечения.

Каустики общего положения в трехмерном пространстве имеют лишь стандартные особенности: “ласточкин хвост”, “пирамида” и “кошелек”. Пирамида имеет три ребра возврата, касающиеся в вершине. У кошелька – только одно ребро возврата, и он состоит из двух носов лодки, пересекающихся по двум линиям. Эти особенности устойчивы.

Задача о движении кластеров. Ранее нами установлено, что крупный фрагмент геля (например, кластер) ведёт себя следующим образом: в силу особенностей реакции рекомбинации в кластерных системах неизбежно требуется третий компонент, который формируется сразу с рекомбинационными взаимодействиями двух соседних кластеров. Этот третий кластер является катализатором, который берет на себя часть энергии и перераспределяет (диссипирует) ее между реагирующими фрагментами. Причем этот третий кластер является значительно более лёгким (то есть подвижным), чем два других. Эти фрагменты перемещается по всему гелево- кластерному объему (то есть по одной спирали или по их группе), и, по-видимому, именно они и отвечает за возникновение токов в неравновесной системе. Эти фрагменты затем вновь рекомбинируют, вместо них возникают новые кластеры уже по диссоциативно-диспропорциональному механизму.

Умозрительно рассмотрим поведение этих нанокластеров, несущих заряд. Возможны разные варианты поведения заряда.

Пусть имеется крупный диполь, образованный первыми двумя фрагментами-кластерами. Этот фрагменты тяжёлые и малоподвижные в сравнении с лёгкими, «потокообразующими» кластерами геля. Диполь имеет вытянутую форму. Со стороны положительного заряда диполя стохастически отщепляется несколько более лёгких фрагментов (Рис. 7).

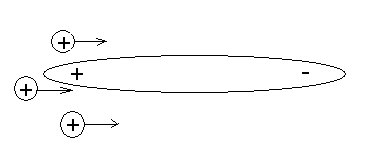
Рис.5. 7.

Под воздействием электрического поля эти фрагменты перемещаются или к другому диполю, или к отрицательно заряженному противоположному концу диполя (Рис.5.8).

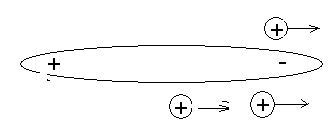
Рис. 5.8.

и поглощаются этим кластерным фрагментом.

После этого на отрицательной части диполя в результате реакции рекомбинации образуются новые, уже отрицательные малые фрагменты, (Рис.5. 9), которые уже рекомбинируют на положительном конце диполя, и начинается перемещение кластеров в противоположном направлении (Риc. 5.10).

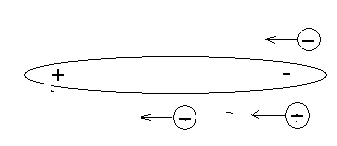
Рис. 5.9.

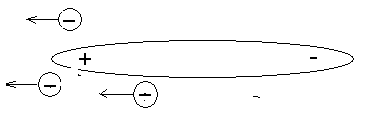
Риc. 5.10.

Рассмотрим теперь обращенное поле диполей, сформировавших кластер. В этом случае диполи можно рассматривать локально упрощенно как цепочки и слои диполей, пренебрегая искривлениями и сложной формой кластеров. При этом можно получить схематически приближенную картина формирования коллоидных слоёв Гуи-Штерна.

Стороны диполей, складывающих слой Штерна определённого знака, можно рассматривать как плоскости, вдоль которых движутся свободные заряды разного знака. Соответственно, здесь можно ввести аналог плазменной частоты – то есть частоты, с которой лёгкие фрагменты движутся между слоями, составленными крупными кластерами. Согласно [15], легкие фрагменты геля не могут далеко отойти от более тяжёлых дальше определённого расстояния, и колеблются возле них с частотой, сходной с плазменной частотой. Следовательно, каждому кластерному фрагменту соответствуют некоторые колебания заряда и колебания тока, вызванные смещением отделившихся свободных частиц. Заметим, что масштаб колебаний тока, определяемого кластером, может быть значителен, так как число фрагментов достаточно велико.

В [20] нами показано, что модели, в которых рассматриваются неупругие соударения кластеров, отображаемые на графитовой плоскости, описываются и соответствуют следующему сценарию, а именно – формированию ударных волн в местах их взаимодействия, например. При этом прослеживаются явления гелевой волновой интерференции или дифракции, когда создаются многообразия движущиеся волновых фронтов [3]. Перестройки этих фронтов суть перестройки наших каустик, исследуемых в “пространстве-времени”. Объединение фронтов в различные моменты времени образует некую гиперповерхность в пространстве – времени. Эта гиперповерхность, образованная типичным движущимся фронтом, сама является фронтом типичного лежандрова отображения некого подмногообразия, размерность которого на 1 больше размерности изучаемого движущегося фронта [11]. Поэтому гиперповерхность в пространстве-времени, образованная фронтами в различные моменты времени, называется большим фронтом. Особенности больших фронтов, образованных в пространстве-времени перестройками в типичных семействах движущихся фронтов, известны. Если исходное пространство трехмерно, то особенности типичных больших фронтов диффеоморфны дискриминантному геометрическому многообразию группы или [1,2,3].

Вместе с тем гелевая волновая интерференция или дифракция размывают действительные размеры и форму сложных кластеров, в момент их отображения (разряда) на графитовой плоскости. Это еще одна особенность поведения движущихся зарядов [19].

Для расчета конкретных частот колебаний и амплитуд возникающих токов необходимы достаточно сложные вычисления, которые, как мы надеемся, выполним в последующих работах.

Таким образом, можно полагать, что ток связан с электрическим полем соотношением . При этом связь между ними колебательная, и, следовательно, существует только в смысле некоторой средней величины. Происходит это потому, что локально, в данной точке или в данный момент времени в соотношении может меняться знак проводимости , так как, в одном случае, меняется тип заряда (первый случай движения), а в другом – связь поля и тока нелинейна и самосогласована (второй способ движения).

Задача о пульсациях. Пусть имеется спиралевидное структурное образование оксигидратного стохастического коллоида. Подобные стохастические образования нами обнаружены на гелях оксигидра иттрия и железа в условиях далеких от равновесия, таблицы 5.2, 5.3. Эти образования могут быть эквивалентно замещены кругом. Так как мы рассматриваем наравновесный гель, то в нём постоянно образуются и поглощаются третьи заряженные частицы [15]. Если частицы образуются со знаком «+», то ток направлен по полю. Период, когда кластерная частицы образуются, соответствует вытеканию тока (или потока) из круга. Это соответствует выплеску третьих кластеров. А так как мы считаем, что спираль (замещённая нами кругом) имеет дипольный момент, то есть собственное электрическое поле, то частица приходит в движение по этому полю, и образует электрический поток или ток в проводниках первого рода, который уже измеряется прибором.

Зная фазовую диаграмму тока (потока кластеров), можно восстановить векторное электрическое поле в точке измерения. Диаграмму тока для исследования геля можно умозрительно представить следующим образом. Измерим токи во все моменты времени за некоторый период. В результате можно получить значение тока по оси, нормальной поверхности электрода, точнее, усредненное значение по поверхности электрода. Обозначим эту ось как ось абсцисс. Затем восстановим по этим характеристикам значения тока в направлениях, параллельных поверхности электрода, и вычислим по полученным данным поле. Для каждого момента времени полученные векторы поля поместим началом в центр координат и рассмотрим векторы. В результате получим диаграмму поля для разных моментов времени. Будем считать, что таким образом можно создать диаграмму электрического поля, действующего в геле.

Это утверждение нуждается в доказательствах.

Действительно, каждый гелевый кластер отправляет (выплескивает) свой «разряд» на электрод. Но сложность состоит в том, что таких объектов в геле достаточно много. Следовательно, если они расположены хаотически (а это предположение естественное, так как гель состоит из большого количества фрагментов, размер которых не превышает микрона, сама же поверхность электрода измеряется в квадратных сантиметрах), то мы должны увидеть картину, напоминающую хаотическое море. Действительно, размеры кластеров могут быть разными, заряды будут достигать углеграфитовой поверхности в разное время, поэтому визуально наблюдается просто хаотическое распределение точек.

Мы это часто и наблюдаем. Тем не менее часть этих точек (рефлексов) распределена неравномерно, то есть среди них есть некоторые выбранные направления. Это несложно видеть на представленных экспериментальных фазовых диаграммах электрического тока. А это означает, что хаотического моря уже нет.

Ранее в [21] нами показаны экспериментальные каустики многообразий потоковых кластеров в гелях оксигидратов железа (II,III) (магнитной жидкости) после старения геля. В экспериментальных каустиках можно выделить следующие перестроечные семейства, близкие или совпадающие с типичными перестройками каустик в трехмерном пространстве лагранжевых многообразий: .

Возможно, если разные кластеры отдают свой заряд в разное время, это явление достаточно редкое, если говорить о крупных всплесках электротока. Но если пытаться рассмотреть все моменты времени, то мы имеем дело с неэлементарным процессом, когда в каждый момент фиксируются разряды многих кластеров. В прежних работах [17] нами показано, что каждый из спиральных наборов обладает дипольным или квадрупольным зарядом [5,6]. И процесс формирования спиралевидных кластеров из всё более крупных диполей может идти до тех пор, пока размеры диполей не станут достаточно велики. Расположение таких диполей уже нельзя назвать случайным, оно не хаотично и подчиняется общему полю в геле. Следовательно, выявив наиболее статистически вероятные поля, можно обнаружить, что на диаграмме некоторые области будут “густо” заполнены экспериментальными точками разряжения кластеров-зарядов. По характеру зачернения можно судить о конфигурации “разряжения” гелевых кластеров, их энергетической симметрии.

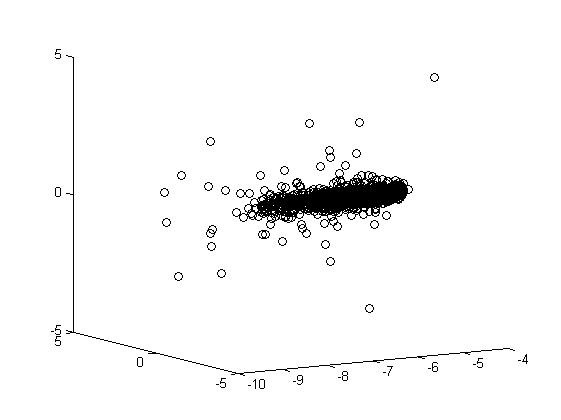
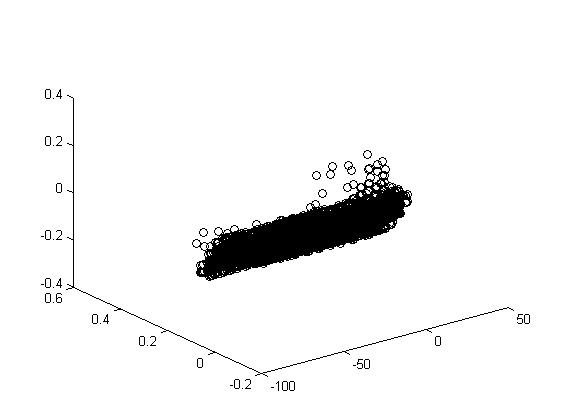
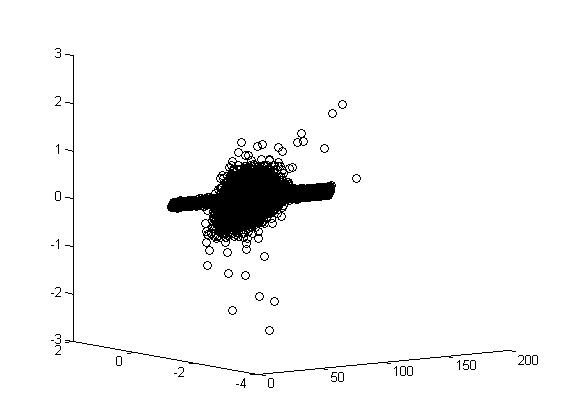
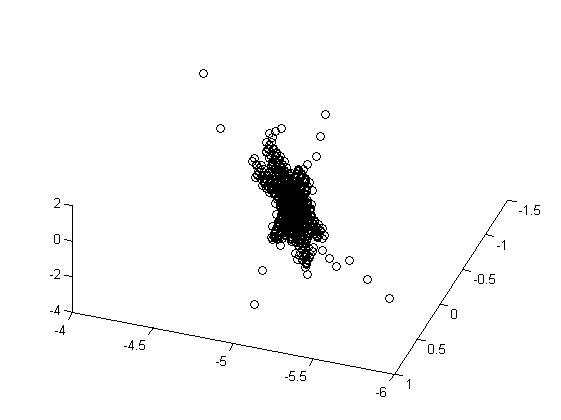
Экспериментальные данные. Результаты экспериментов приведены в виде таблицы рисунков 5.1 и в таблицах 5.2, 5.3, 5.4. Отметим, что фазовые диаграммы (по осям – величина тока, производная тока по времени, вторая производная тока по времени) – почти плоские, то есть вторая производная представляется достаточно малозначительной.

Заметим, что эти представления не являются точными: для более адекватного отображения необходимо решать обратную задачу электростатического потенциала. Сама задача предполагает более точную постановку в математической её части. Поэтому ограничимся качественными построениями, которые, на наш взгляд, тем не менее, дают определённые и очень наглядные представления общей картины распределения зарядов по графитовой поверхности.

Таблица 5.1

Некоторые экспериментальные данные размещения ряда кластерных мультиполей на примере оксигидрата циркония.

Эксперимент 8 сентября 2010 года	«Энергетическое веретено». Соответствует рисунку 2, справа. – вытянутый длинный диполь или квадруполь, гель оксигидрата циркония.
Эксперимент 10 сентября 2010 года	«Энергетическое веретено». Соответствует рисунку 2, справа. – вытянутый длинный диполь или квадруполь, или «обойма» из них, гель оксигидрата циркония.
Эксперимент 10 сентября 2010 года	Сложная энергетическая конфигурация. Группа диполей, свернувшаяся спиралью, с прикреплёнными к ней на концах длинными диполями.
	«Звезда». Три диполя или квадруполя, соединённые в середине под углом в 60 градусов друг к другу.

На экспериментальных каустиках оксигидрата железа (II,III) и оксигидрата иттрия таблицы 2,3 , можно выделить кластерные перестроечные семейства, близкие или совпадающие с типичными перестройками каустик в трехмерном пространстве лагранжевых многообразий: . Следовательно, можно сказать, что кластеры геля, или их энергетические лагранжианы - каустики свидетельствуют об определённой упорядоченности нанокластеров, их кристалличности, хотя и имеют элементы хаоса, таблица 5.4. Представленные в таблице 5.4 метаморфозы каустик оксигидрата железа (III), движущихся в трехмерном пространстве, получаются сечениями больших (трехмерных) каустик в четырехмерном пространстве-времени, называемые изохронами.

Съемки фазовых портретов оксигидрата железа (III) на установке с вращающимся графитовым электродом и измерительной системой ZETLab, позволили обнаружить доменную природу строения этой коллоидной системы. Такая доменная разообщенность хорошо прослеживается на рис.5.11. Экспериментальные домены на рис.5.11 ограничены вертикальными линиями, которые характеризуют падение потенциала на границе домена до низших значений. Фазовые портреты, построенные выборочно для двух случайных доменов (a,b), оказываются близкими по геометрической форме. Ширина доменных областей геля различается ненамного.

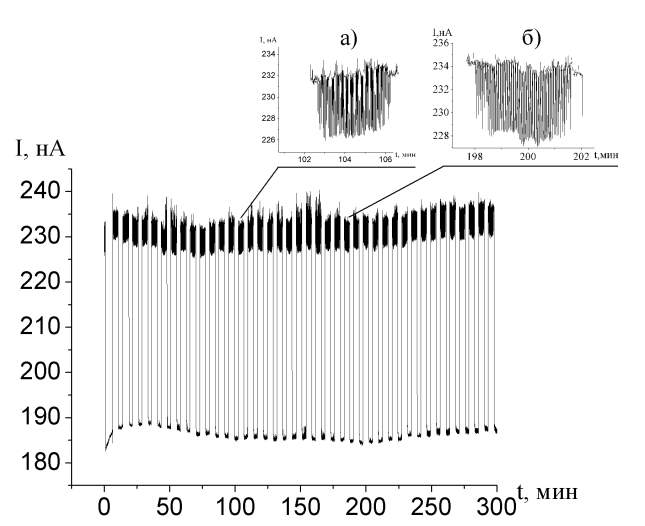
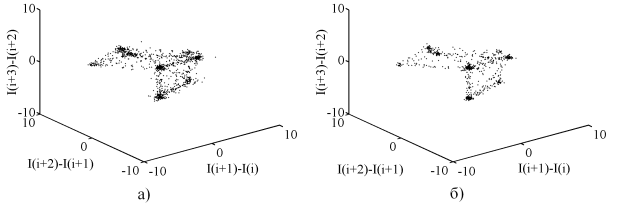
a) Рис.5.11. b)

Доменно-кластерная природа гелей оксигидрата железа