
- •Глава 1. Оператор Лизеганга
- •Оператор Лизеганга как отражение колебательных свойств гелевых полимерных систем. Введение оператора Лизеганга.
- •1.2.Исследование сильно нелинейного уравнения диффузии
- •1.3. Упрощённая запись оператора Лизеганга
- •Графики для разных значений и . На графике слева приведены значения , справа - . По оси абсцисс отложено время, по оси ординат – значение в безразмерных единицах.
- •График стационарного решения задачи (1.3.5)-(1.3.6). По оси абсцисс отложена безразмерная координата X, по оси ординат – функции и , согласованные при , также в безразмерных единицах.
- •1.5 Оператор Лизеганга и некоторые экспериментальные данные
- •Глава 2 Оптические свойства гелевых оксигидратов и размеры кластеров
- •2.1 Уравнение поглощения света на конформерных “шумовых” кластерах.
- •Концентрационная зависимость кластеров от времени для простейшей спирали.
- •Изменение интенсивности волн прошедшего поля через оксигидратные кластеры в пространстве.
- •2.3 Влияние пульсационного шума или тока самоорганизации в магнитном поле на особенности оптических характеристик окигидрата иттрия.
- •2.4 Кинетические кривые оптической плотности некоторых гелей оксигидратных систем
- •Спектры поглощения силикагелей
- •2.5. Интерферационный подход к экспериментальнолму определению
- •2.6. Вычисления размеров кластеров на примере гелей оксигидрата кремния и иттрия.
- •Зависимости оптической плотности смешанных гелей оксигидрата кремния и оксигидрата иттрия от времени.
- •Глава 3 Каустики стохастических потоковых кластеров и решение задачи формообразования самих кластерных частиц.
- •Глава 4. Каустики лагранжевых отображений гелевой оксигидратной магнитной жидкости железа
- •4.1 Введение
- •4.2 Типичные перестройки каустик в трехмерном пространстве лагранжева многообразия
- •Литература
- •Глава 5 Форма и механизм разряда волновых стохастических кластеров вблизи регистрирующих электродов
- •Результаты и их обсуждение
- •Волновые домены гелей оксигидрата железа,
- •Фазовые портреты двух доменов, указанных стрелками
- •Оксигидрат железа (III)
Литература
1. П.Берже, И.Помо, К.Видаль, Порядок в хаосе. Изд. М.: Мир, 1991,с.367
2. Малинецкий Г.Г., Потапов А.Б. Современные проблемы нелинейной динамики. М.: Едиториал УРСС, 2002. 360 с.
3. Арнольд В.И. Особенности каустик и волновых фронтов.М.: ФАЗИС.1996. 334с.
4. Арнольд В.И. Теория катастроф. Изд. 4-е, стереотипное. – М.: Едиториал УРСС,2004.128с.
5. Yuri I. Sucharev. Wave Oscillations in Colloid Oxyhydrates // Switzerland, UK, USA: Trans Tech Publications LTD. 2010. 497p.
6. Yuri I. Sucharev. Nonlinearity of Colloid Systems: Oxyhydrate Systems. Switzerland, UK, USA: Trans Tech Publications. 2007. 433p.
7. Сухарев Ю.И., Марков Б.А. Нелинейность гелевых оксигидратных систем. Екатеринбург: УрОРАН. 2005. 468с.
8. Сухарев Ю.И., Верцюх Е.С. Тонкопленочные покрытия графитовых подложек в коллоидно-химических оксигидратных гелях в условиях некоррелированных цепочечных рэтчетов. Бутлеровские сообщения. 2012. Т.29. №2. С.75-86.
9. Сухарев Ю.И, Марков Б.А. Шумовые пульсации в оксигидратных системах. Челябинск: Изд. Челябинского государственного университета Синтез и применение специфических оксигидратных сорбентов. 2012. 160с.
10. Сухарев Ю. И. , Тарамина Е. В. , Кузнецов А. Л. , Апаликова И. Ю. Cтохастический самопроизволный выплеск кластеров в оксигидратной коллоидной системе железа(III) и изменение динамической вязкости во времени. Бутлеровские сообщения. 2012. Т.29. №1. С.22-35.
11. В.С. Анищенко, В.В. Астахов, Т.Е. Вадивасова и др. Нелинейные эффекты в хаотических и стохастических системах. Москва-Ижевск: Институт компьютерных исследований.2003.-529с.
12. Розенцвейг Р. Феррогидродинамика: Пер.с анг.-М.: Мир,1989.-356с.
13. Сухарев Ю.И., Марков Б.А., Лебедева И.Ю., Шарфунов И.А. Шумовые почти периодические колебания в оксигидратах d- и f-элементов // Журн. Бутлеровские сообщения.2009.Т.18.№8.С.36-48.
14. Сухарев Ю. И. , Верцюх Е. С. Сравнительные схемы работы кластерных потоков при изучении фазовых портретов коллоидно-химических систем. Бутлеровские сообщения. 2012. Т.30. №4. С.1-16.
Глава 5 Форма и механизм разряда волновых стохастических кластеров вблизи регистрирующих электродов
Периодические процессы в коллоидной химии чрезвычайно распространены, учитывая их практически всеохватное распространение и изучение [3]. Эта роль отводится когерентной химии, то есть химии колебательно-периодических процессов. Но при этом есть определённая сложность: в классической неорганической химии и коллоидной химии колебательная парадигма развития явлений и процессов практически не разработана и не понята. Следовательно, мы упускаем из поля зрения многие тонкие коллоидно-химические явления, которые могут быть весьма существенными и значимыми при адсорбции и катализе, например. Гелевые оксигидратные системы (ГОС) редкоземельных элементов, а также оксиды-гидроксиды некоторых d – элементов, таких как цирконий, ниобий, титан и другие, интересны тем, что, являясь весьма труднорастворимыми, склонны к диссоциации по кислотно-основному механизму, а, следовательно, к проявлению ионообменных и адсорбционных свойств. Их свойства слабо или совсем не воспроизводимы, хотя, казалось бы, предприняты все условия и средства для полного воспроизведения начальных параметров.
Исследования нелинейных свойств подобных гелевых оксигидратных систем обнаружили следующие особенности: колебательную дилатантность, колебательную (пульсационную) электрическую проводимость, самопроизвольный электроток гелевой самоорганизации на фоне поляризационных явлений, окрашенность гелевых систем, колебательные оптические и сорбционные свойства и многое другое, с чем можно познакомиться на нашем сайте (http//: oxyhydrate-gel.ru), а также в наших крупных работах [4,5,6].
Эволюция многих систем, в том числе и коллоидных, может быть описана системой обыкновенных дифференциальных уравнений изменения некоторых регистрируемых параметров, как-то описывающих коллоидную систему:
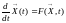 (5.1)
(5.1)
где
![]() -
вектор в фазовом пространстве,
-
вектор в фазовом пространстве,
![]() -
векторное поле в этом пространстве.
Именно такой вид имеют законы, управляющие
поведением различных осцилляторов, в
том числе и генератора Ван-дер-Поля.
Система дифференциальных уравнений,
например, система (1) называется потоком
в
-
векторное поле в этом пространстве.
Именно такой вид имеют законы, управляющие
поведением различных осцилляторов, в
том числе и генератора Ван-дер-Поля.
Система дифференциальных уравнений,
например, система (1) называется потоком
в
![]() Если
не
зависит явно от времени, а зависит только
от
Если
не
зависит явно от времени, а зависит только
от
(![]() ),
то поток называется автономным. Найти
аналитическое выражение для уравнений
(1) удается лишь в отдельных частных
случаях, когда поток интегрируем.
Рассмотрим соответствующую потоку
траекторию в фазовом пространстве.
Упрощая задачу, используем подход,
развитый Анри Пуанкаре. Вместо прямого
изучения решения системы уравнений (1)
в R3
просто рассмотрим точки пересечения
траектории с плоскостью. Отметим, что
точки пересечения соответствуют
заданному направлению эволюции. Выбираем
плоскость S, заданную уравнением
),
то поток называется автономным. Найти
аналитическое выражение для уравнений
(1) удается лишь в отдельных частных
случаях, когда поток интегрируем.
Рассмотрим соответствующую потоку
траекторию в фазовом пространстве.
Упрощая задачу, используем подход,
развитый Анри Пуанкаре. Вместо прямого
изучения решения системы уравнений (1)
в R3
просто рассмотрим точки пересечения
траектории с плоскостью. Отметим, что
точки пересечения соответствуют
заданному направлению эволюции. Выбираем
плоскость S, заданную уравнением
![]() ,
и отмечаем точки пересечения траектории
орбиты
,
и отмечаем точки пересечения траектории
орбиты
![]() (решения
уравнения (5.1) с плоскостью S, соответствующие
заданному направлению эволюции (
(решения
уравнения (5.1) с плоскостью S, соответствующие
заданному направлению эволюции (![]() ).
Траектория
пересекает
S в точках
).
Траектория
пересекает
S в точках
![]() [7].
[7].
Таким образом, можно использовать множество точек, образующих сечение Пуанкаре, то есть граф в двух измерениях. В оксигидратных гелях мы зачастую имеем дело с ионными потоковыми движениями. Даже при достаточно низкой температуре (298К) поляризованные ДЭС макромолекул, имеющих пептизационно - полимеризационные конформеры, при развитии во времени либо разрушаются (“разрываются”) с выплеском ионно-молекулярных потоков, либо поглощают их. Причины этого — чисто термодинамические, при макромолекулярных пептизационно - полимеризационно - конформерных перестройках энергия ДЭС, окружающих их, стремится к минимизации. Это достигается либо выплеском ионных потоков, либо их связыванием (причем, в узких областях пространства, то есть в условиях далеких от равновесия).
Таким образом, в гелевых образцах оксигидрата иттрия, циркония и других наблюдается сложная система конформерного движения самих макромолекулярных образований и потокового ионно-кластерно-молекулярного движения внутри них. В качестве отображающей плоскости принимается или графитовый, или платиновый электроды, на которых замыкается ионно-молекулярный кластерный поток (“протыкает” их).
Приведенные
в наших работах [8,9,10] каустики
(энергетическое отображение ионных
потоков) вполне структурно очерчены.
Модели, в которых рассматриваются
(неупругие) соударения кластеров (то
есть составляющих частиц) описываются
и соответствуют формированию ударных
волн в форме гелевых каустик в местах
их взаимодействия, например. Эти
энергетические рефлексы суть явления
гелевой волновой интерференции или
дифракции [3]. При этом создаются
многообразия движущихся волновых
фронтов. Перестройки этих фронтов есть
перестройки наших каустик, исследуемых
в “пространстве-времени”. Объединение
фронтов в различные моменты времени
образует некую гиперповерхность в этом
пространстве. Эта гиперповерхность,
образованная типичными движущимися
фронтами, сама является фронтом типичного
лежандрова отображения подмногообразия,
размерность которого на 1 больше
размерности изучаемого движущегося
фронта [11]. Поэтому гиперповерхность в
пространстве-времени, образованная
фронтами в различные моменты времени,
будет называться большим фронтом.
Особенности больших фронтов, образованных
в пространстве-времени перестройками
в типичных семействах движущихся
фронтов, известны. То есть если исходное
пространство трехмерно, то особенности
типичных больших фронтов диффеоморфны
дискриминантному многообразию группы
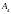 или
или
 [1,2,6].
Возможны также трансверсальные их
самопересечения.
[1,2,6].
Возможны также трансверсальные их
самопересечения.
В современной теории динамических систем известно [12,13], что в двухмерной гидродинамике (в том числе коллоидных растворов) могут существовать перемещения кластеров, которые (перемещения) имеют симметрию или квазисимметрию [14]. Это связано с тем, что гамильтоновские системы в общем случае являются “носителями хаоса”. Это значит, что при некоторых минимальных ограничениях фазовое пространство некоторой динамической оксигидратной гамильтоновской системы имеет области, внутри которых происходит движение с перемешиванием. Если же такая гамильтоновская система явно зависит от времени, то эта зависимость является периодической.
Удивительное
достижение современной физики
 сосуществование в фазовом пространстве
областей устойчивой динамики и областей
хаоса.
Зародышем хаоса, как отмечают Г.М.
Заславский и Р.З.Согдеев, являются
стохастические слои, образующиеся в
окрестности разрушенных сепаратрис
колебательного движения при их толчковом
возмущении. Области разрушения сепаратрис
соотвентствуют и областям разрыва
донорно-акцепторных связей (водородных
связей) в оксигидратных кластерных
системах. При стохастическмм возмущении,
сопровождающем разрушение сепаратрис,
наблюдается формирование стохастического
резонанса. Образование стохастического
слоя при возмущении нелинейного гелевого
осциллятора является практически
обязательным. Развитие данных представлений
позволило нам для оксигидратных гелей
высказать идею и ее математически
обосновать - идею вычисления размеров
некоторых организаций оксигидрата
(пейсмекеров) [5], а также предположить
различающиеся симметрии гелевых волн,
образованных диффузионно перемещающимися
оксигидратными кластерами, сформированными
по диссоциативно-диспропорциональному
механизму [15]. Толчковые явления при
этом определяются выбросом третьих
кластерных (в основном нанокластерных)
частиц, которые отвечают за диссипацию
энергии системы [16] в целом.
сосуществование в фазовом пространстве
областей устойчивой динамики и областей
хаоса.
Зародышем хаоса, как отмечают Г.М.
Заславский и Р.З.Согдеев, являются
стохастические слои, образующиеся в
окрестности разрушенных сепаратрис
колебательного движения при их толчковом
возмущении. Области разрушения сепаратрис
соотвентствуют и областям разрыва
донорно-акцепторных связей (водородных
связей) в оксигидратных кластерных
системах. При стохастическмм возмущении,
сопровождающем разрушение сепаратрис,
наблюдается формирование стохастического
резонанса. Образование стохастического
слоя при возмущении нелинейного гелевого
осциллятора является практически
обязательным. Развитие данных представлений
позволило нам для оксигидратных гелей
высказать идею и ее математически
обосновать - идею вычисления размеров
некоторых организаций оксигидрата
(пейсмекеров) [5], а также предположить
различающиеся симметрии гелевых волн,
образованных диффузионно перемещающимися
оксигидратными кластерами, сформированными
по диссоциативно-диспропорциональному
механизму [15]. Толчковые явления при
этом определяются выбросом третьих
кластерных (в основном нанокластерных)
частиц, которые отвечают за диссипацию
энергии системы [16] в целом.
Экспериментальная часть.
Прибор для измерения импульсного поляризационного электрического тока, сформированного перемещающимися потоками нанокластеров в статических условиях, состоит из прямоугольной ячейки, на концах которой закрепляли графитовые электроды (рис.5. 2). Контакты электродов подключали к электронному регистрирующему блоку. Свежеприготовленный гель помещали в эту ячейку. Расстояние между электродами составляло 70 мм или меньше. При этом ячейка, содержащая гель, замыкалась практически накоротко, величина омического сопротивления была незначительной (15-20, кОм). Эксперимент проводили в течение 5 часов. Процесс термостатировали (Т = 303К)[15].
Все токоподводящие шины бронировали от внешних электромагнитных наводок. Для анализа токовых процессов, протекающих в гелевой фазе, временной интервал между замерами должен быть небольшим. С этой целью использовали модульные измерительные системы L-CARD c модулем E-270 c частотой опроса 5 замеров в с., а также измерительную систему ZETLab, включающую усилитель ZET410 с измерительным блоком ZET 210. Данные модули являются современными универсальными прогрммно-аппаратными устройствами для использования со стандартной шиной USB и предназначенными для построения многоканальных измерительных систем ввода, вывода и обработки цифровой информации в составе персональных IBM - совместимых компьютеров.
Рассмотренная
электрохимическая ячейка позволяет
получать некие стационарные точки
Пуанкаре [15], так как регистрирующие
электропроводящие графитовые пластины
неподвижны. Поэтому к недостаткам такой
электрохимической ячейки ((рис.5.1)(b))
можно отнести отсутствие перемешивания
в системе и, следовательно, неподвижность
плоскости пересечения с кластерными
орбитами для снятия точек Пуанкаре.
Вместо прямого изучения решения системы
уравнений (5.1) в R3
просто рассмотрим точки пересечения
траектории с электропроводящей графитовой
плоскостью. Отметим, что последовательность
точек пересечения соответствует
заданному направлению эволюции. Выбираем
графитовую плоскость
,
заданную уравнением
 ,
и отмечаем точки пересечения траектории
орбиты
(решения уравнения (5.1) с плоскостью
,
соответствуют заданному направлению
эволюции (
,
и отмечаем точки пересечения траектории
орбиты
(решения уравнения (5.1) с плоскостью
,
соответствуют заданному направлению
эволюции (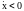 ).
Траектория
).
Траектория
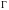 пересекает
в точках
пересекает
в точках
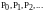 .
.
Таким образом, можно получить множество точек, образующих сечение Пуанкаре, то есть граф в двух измерениях. В оксигидратных гелях мы имеем дело именно с ионными потоковыми движениями. Как нам представляется, для получения объемных фазовых изображений заряженных кластеров оксигидратных частиц необходимо получить точки (сечения) Пуанкаре всего объемно-пространственного кластерного габитуса. Для этого секущая поверхность или поверхности должны перемещаться в пространстве по определенному, известному закону, нормально пересекая орбиты движущихся кластеров.
С этой целью создана установка с вращающимся графитовым цилиндрическим электродом, представленная на рис. 5.1(а) и приставка к прибору, показанная на рис.5.3 в форме стакана с вклеенным электродом круглого сечения на его дне


а) b)
Рис.5.1. Фотографии экспериментальных коллоидно-химических ячеек для снятия спайковых выплесков тока самоорганизации оксигидратных гелей с вращающимся графитовым электродом (a) и неподвижными электродами (b) ;

Рис. 5.2. Графитовая вставка в коаксиальном металлическом цилиндре;

Рис.5.3. Фотография нижнего пластикового стакана с встроенным неподвижным графитовым электродом.
Относительно этого неподвижного электрода (рис.5.3) замеряли разность потенциалов вращающего графитового электрода, который снабжен электросъемниками прижимного действия. На рис.5.1(a) эти электросъемники прижимного действия хорошо различимы.
Можно представить себе два способа построения нанотоковых точек пересечения Пуанкаре [7]:
Потенциал снимается только с горизонтальных графитовых электропроводящих неподвижных пластин, рис.5.1 (b).
Потенциалы или нанотоковые выплески регистрируются непосредственно с элекросъемников прижимного действия (рис.5.1(a)) и вторым неподвижным электродом круглого сечения, помещенным на дне ячейки, подобной рис. 5.3, при вращающейся цилиндрической графитовой вставке.
В дальнейшем будем просто говорить, что исследовательская работа выполнялась
по схемам 1, или 2.
